Oligopole: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Auf einem Oligopolmarkt existiert angebotsseitig Marktmacht. Diese entsteht, wenn auf einem Markt viele Nachfrager, jedoch wenige Anbieter agieren. Auch diese wenigen Anbieter stehen im Wettbewerb zueinander. Hierbei können sich die vertriebenen Produkte unterscheide (differenzierte Güter) oder auch nicht (homogene Güter), wobei es darauf ankommt ob sich die Unternehmen in einem Preis- oder Mengenwettbewerb befinden. <br> | Auf einem Oligopolmarkt existiert angebotsseitig Marktmacht. Diese entsteht, wenn auf einem Markt viele Nachfrager, jedoch wenige Anbieter agieren. Auch diese wenigen Anbieter stehen im Wettbewerb zueinander. Hierbei können sich die vertriebenen Produkte unterscheide (differenzierte Güter) oder auch nicht (homogene Güter), wobei es darauf ankommt ob sich die Unternehmen in einem Preis- oder Mengenwettbewerb befinden. <br> | ||
Zur Vereinfahung soll es im Weiteren um die simpelste Form des Oligopols gehen: dem Dyopol | Zur Vereinfahung soll es im Weiteren um die simpelste Form des Oligopols gehen: dem Dyopol | ||
| + | |||
| + | __TOC__ | ||
==Cournot Wettbewerb== | ==Cournot Wettbewerb== | ||
| Zeile 6: | Zeile 8: | ||
Im [[Perfekten Wettbewerb]] ergab sich folgende [[Nachfrage|Nachfragefunktion]]: <math> P(Q)=a-bQ </math> <br> | Im [[Perfekten Wettbewerb]] ergab sich folgende [[Nachfrage|Nachfragefunktion]]: <math> P(Q)=a-bQ </math> <br> | ||
Die Nachfragefunktion ändert sich im Dyopol nicht, jedoch stellt sich die Gesamtmenge Q aus der Produktion aller Unternehmen zusammen. Bei zwei Untrnehmen ergibt das <math> P(q_1,q_2)=a-b(q_1+q_2)=a-bq_1-bq_2 </math>. Die Gewinnfunktion bleibt unverändert bei Umsatz abzüglich der Kosten. Unter der Annahme von Grenzkosten gleich null ergibt sich: <br> | Die Nachfragefunktion ändert sich im Dyopol nicht, jedoch stellt sich die Gesamtmenge Q aus der Produktion aller Unternehmen zusammen. Bei zwei Untrnehmen ergibt das <math> P(q_1,q_2)=a-b(q_1+q_2)=a-bq_1-bq_2 </math>. Die Gewinnfunktion bleibt unverändert bei Umsatz abzüglich der Kosten. Unter der Annahme von Grenzkosten gleich null ergibt sich: <br> | ||
| − | <math> \pi_1=pq_i=(a-bq_1-bq_2)q_1 </math> und | + | <math> \pi_1=pq_i=(a-bq_1-bq_2)q_1 </math> und <br> |
<math> \pi_2=pq_i=(a-bq_1-bq_2)q_2 </math> <br> | <math> \pi_2=pq_i=(a-bq_1-bq_2)q_2 </math> <br> | ||
Beide Unternehmen maximieren ihren Gewinn in Bezug auf ihrer Produktionsmenge. Hierfür wird die Gewinfunktion nach der Menge abgeleitet. Da Unternehmen nur ihre eigene Menge wählen können, ist die Menge des anderen Unternehmens eine Konstante. Beide Gewinnfunktionen sind symmetrisch, daher wird im Folgenden lediglich Unternehmen 1 betrachtet. <br> | Beide Unternehmen maximieren ihren Gewinn in Bezug auf ihrer Produktionsmenge. Hierfür wird die Gewinfunktion nach der Menge abgeleitet. Da Unternehmen nur ihre eigene Menge wählen können, ist die Menge des anderen Unternehmens eine Konstante. Beide Gewinnfunktionen sind symmetrisch, daher wird im Folgenden lediglich Unternehmen 1 betrachtet. <br> | ||
| Zeile 15: | Zeile 17: | ||
<math>q_2(q_1)=\frac{a}{2b}-\frac{1}{2}q_1</math> <br> | <math>q_2(q_1)=\frac{a}{2b}-\frac{1}{2}q_1</math> <br> | ||
Beide Reaktionsfunktionen zeigen, dass die Relation zwischen der eigenen gewinnmaximalen Menge und der Menge des anderen Unternehmens negativ ist. Je mehr Unternehmen 2 produziert, desto weniger sollte Unternehmen 1 produzieren. Die beiden Reaktionsfunktionen lassen sich auch grafisch darstellen. <br> | Beide Reaktionsfunktionen zeigen, dass die Relation zwischen der eigenen gewinnmaximalen Menge und der Menge des anderen Unternehmens negativ ist. Je mehr Unternehmen 2 produziert, desto weniger sollte Unternehmen 1 produzieren. Die beiden Reaktionsfunktionen lassen sich auch grafisch darstellen. <br> | ||
| − | Datei:Cournot.png| | + | [[Datei:Cournot.png|401px|rahmenlos]] <br> |
<br clear=all> | <br clear=all> | ||
| − | Die in grün eingezeichnete Gerade ist die Reaktionsfunktion von Unternehmen 1 und die in blau eingezeichnet von Unternehmen 2. Angenommen Unternehmen 2 produziert eine Menge <math> q_2 </math>. Die gewinnmaximale Menge von Unternehmen 1 kann in der grünen Funktion abgelesen werden und liegt bei <math> q_1 </math>. | + | Die in grün eingezeichnete Gerade ist die Reaktionsfunktion von Unternehmen 1 und die in blau eingezeichnet von Unternehmen 2. Angenommen Unternehmen 2 produziert eine Menge <math> q_2' </math>. Die gewinnmaximale Menge von Unternehmen 1 kann in der grünen Funktion abgelesen werden und liegt bei <math> q_1' </math>. Unternehmen 2 würde wiederum die eigene Menge anpassen, sodass die Reaktionen entlang der Reaktionsfunktionen in den gestrichelten Linien ersichtlich ist. Im Schnittpunkt ist die produzierte Menge bereits die beste Antwort auf die Produktionsmenge des anderen Unternehmens. In diesem Punkt befindet sich das Cournot-[[Nash Gleichgewicht]]. |
| + | ==Betrand Wettbewerb== | ||
| + | Der Betrand Wettbewerb wird auch Preiswettbewerb genannt. Die strategische Variable, über die die Unternehmen ihren Gewinn maximieren ist der Preis (<math style="inline"> \frac{\part \pi_i}{\part p_i}</math>). <br> | ||
| + | In der Betrachtung wie Unternehmen ihren Gewinn maximieren musss zwischen differenzierten und homogenen Gütern unterschieden werden. <br> | ||
| + | <br> | ||
| + | '''Homogene Güter''' <br> | ||
| + | Homogene Güter sind Güter, bei denen Konsumenten keine Präferenzen für eines der Güter haben. Dies unterscheidet sich nur minimal von der Definition der [[Präferenzenarten#Prfekte Substitute|Substitute]]. Konsumenten sind indifferent zwischen dem Konsum des Gutes von Unternehmen 1 und von Unternehmen 2. Das einzige Entscheidungskriterium ist daher der Preis. Ist das Gut von Unternehmen 1 günstiger als von Unternehmen 2, so kauft der Konsument das Gut von Unternehmen 1 und andersherum. Dies stellt sich als Anreiz für beide Unternehmen dar, sich minimal zu unterbieten und so die gesamte Marktnachfrage auf sich zu ziehen. Solange der Preis überhalb der [[Kostenarten#Grenzkosten|Grenzkosten]] liegt nehmen beide Unternehmen an dem Preiwettbewerb teil. Haben beide Unternehmen identische Grenzkosten, stellt sich der Marktpreis bei den Grenzkosten ein. Hat ein Unternehmen etwas höhere Grenzkosten, so liegt der Marktpreis bei den höheren Grenzkosten. <br> | ||
| + | ''Beispiel'': Unternehmen 1 hat Grenzkosten von a und Unternehmen Grenzkosten von b, wobei <math> a<b </math>. Beide Unternehmen können sich so lange Unterbieten, bis der Marktpreis bei b liegt. Unternehmen 2 kann nun nicht mehr unterbieten, da es sonst mit jeder Einheit Verlust macht. Unternehmen bietet einen Preis minimal unterhalb von b an. <math> P=b-\varepsilon </math>, wobei <math> \varepsilon </math> gegen 0 strebt, da Unternehmen 1 einen Anreiz hat die Grenzkosten möglichst gering zu unterbieten. Daher <math> \lim\limits_{\varepsilon \rightarrow 0}{b-\varepsilon}=b </math>. <br> | ||
| + | <br> | ||
| + | '''Differenzierte Güter''' <br> | ||
| + | Konsumenten haben bei differenzierten Gütern Präferenzen gegenüber den Gütern. In diesem Fall begegnen beide Unternehmen nicht mehr zwangsläufig der selben [[Nachfrage]]. <br> | ||
| + | ''Beispiel'': Vielen Nachfragern ist es nicht egal, ob sie Sportsachen von Nike oder von Adidas tragen, einige präferieren Nike und andere Adidas. Die Nachfrage der beiden Konzerne ist nicht [[Elastizitäten#Preiselastizität der Nachfrage|vollkommen elastisch]]. Ihre Nachfrage ist jedoch auch nicht vollkommen unelastisch, denn sollte der Preis von Nike zu groß sein, werden auch die größten Nike Fans irgendwann zu Adidas wechseln. Andersherum steigt die Nachfrage nach Nike Artikeln, wenn Adidas seine Preise anhebt. Die eigene Nachfrage hat also eine negative Relation mit dem eigenen Preis und eine positive mit dem Preis der anderen Unternehmen. <br> | ||
| + | Allgemein gilt <br> | ||
| + | <math> q_1=a-bp_1+cp_2</math> <br> | ||
| + | <math> q_2=a-bp_2+cp_2</math> <br> | ||
| + | In dem oben geschilderten Fall wird Symmetrie angenommen, dies muss aber nicht zwangsläufig vorliegen. Symmetrie bedeutet, dass die Nachgefragte Menge von Unternehmen 1 im selben Maß vom eigenen Preis (<math>p_1</math>) abhängt, wie die Nachfrage von Unternehmen 2 vom eigenen Preis (<math>p_2</math>).<br> | ||
| + | Aufgrund der Symmetrie genügt die Betrachtung von Unternehmen 1 um das Verständnis des Preiswettbewerbs mit differenzierten Gütern zu verstehen. <br> | ||
| + | <math> \pi_1=p_1*q_1=p_1(a-bp_1+cp_2)</math> <br> | ||
| + | <math> \frac{\part \pi_1}{\part p_1}=a-2bp_1+cp_2=0</math> <br> | ||
| + | Umstellen nach <math> p_1 </math> ergibt erneut eine '''Reaktionsfunktion''', die abhängig von dem Preis des anderen Unternehmens ist. <br> | ||
| + | <math> p_1(p_2)=\frac{a}{2b}+\frac{c}{2b}p_2 </math> <br> | ||
| + | <math> p_2(p_1)=\frac{a}{2b}+\frac{c}{2b}p_1 </math> <br> | ||
==Stackelberg== | ==Stackelberg== | ||
Version vom 26. Juni 2023, 13:05 Uhr
Auf einem Oligopolmarkt existiert angebotsseitig Marktmacht. Diese entsteht, wenn auf einem Markt viele Nachfrager, jedoch wenige Anbieter agieren. Auch diese wenigen Anbieter stehen im Wettbewerb zueinander. Hierbei können sich die vertriebenen Produkte unterscheide (differenzierte Güter) oder auch nicht (homogene Güter), wobei es darauf ankommt ob sich die Unternehmen in einem Preis- oder Mengenwettbewerb befinden.
Zur Vereinfahung soll es im Weiteren um die simpelste Form des Oligopols gehen: dem Dyopol
Cournot Wettbewerb
Der Cournot Wettbewerb wird auch als Mengenwettbewerb bezeichnet. In diesem ist die strategische Variable über die die Unternehmen ihren Gewinn maximieren die Produktionsmenge (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part \pi_i}{\part q_i}}
).
Im Perfekten Wettbewerb ergab sich folgende Nachfragefunktion: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(Q)=a-bQ }
Die Nachfragefunktion ändert sich im Dyopol nicht, jedoch stellt sich die Gesamtmenge Q aus der Produktion aller Unternehmen zusammen. Bei zwei Untrnehmen ergibt das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(q_1,q_2)=a-b(q_1+q_2)=a-bq_1-bq_2 }
. Die Gewinnfunktion bleibt unverändert bei Umsatz abzüglich der Kosten. Unter der Annahme von Grenzkosten gleich null ergibt sich:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_1=pq_i=(a-bq_1-bq_2)q_1 }
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_2=pq_i=(a-bq_1-bq_2)q_2 }
Beide Unternehmen maximieren ihren Gewinn in Bezug auf ihrer Produktionsmenge. Hierfür wird die Gewinfunktion nach der Menge abgeleitet. Da Unternehmen nur ihre eigene Menge wählen können, ist die Menge des anderen Unternehmens eine Konstante. Beide Gewinnfunktionen sind symmetrisch, daher wird im Folgenden lediglich Unternehmen 1 betrachtet.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part \pi_1}{\part q_1}=a-2bq_1-bq_2=0 }
Umstellen nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_1}
ergibt eine Funktion, die abhängig von der Produktionsmenge des Unternehmens 2 ist. Diese Funktion beschreibt, welche Menge Unternehmen 1 gewinnmaximal setzen sollte, für jede Produktionsmenge von Unternehmen 2. Diese Funktion ist die Reaktionsfunktion.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_1(q_2)=\frac{a}{2b}-\frac{1}{2}q_2}
aufgrund der Symmetrie:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_2(q_1)=\frac{a}{2b}-\frac{1}{2}q_1}
Beide Reaktionsfunktionen zeigen, dass die Relation zwischen der eigenen gewinnmaximalen Menge und der Menge des anderen Unternehmens negativ ist. Je mehr Unternehmen 2 produziert, desto weniger sollte Unternehmen 1 produzieren. Die beiden Reaktionsfunktionen lassen sich auch grafisch darstellen.
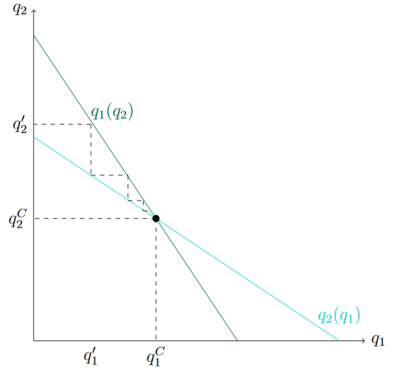
Die in grün eingezeichnete Gerade ist die Reaktionsfunktion von Unternehmen 1 und die in blau eingezeichnet von Unternehmen 2. Angenommen Unternehmen 2 produziert eine Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_2' }
. Die gewinnmaximale Menge von Unternehmen 1 kann in der grünen Funktion abgelesen werden und liegt bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_1' }
. Unternehmen 2 würde wiederum die eigene Menge anpassen, sodass die Reaktionen entlang der Reaktionsfunktionen in den gestrichelten Linien ersichtlich ist. Im Schnittpunkt ist die produzierte Menge bereits die beste Antwort auf die Produktionsmenge des anderen Unternehmens. In diesem Punkt befindet sich das Cournot-Nash Gleichgewicht.
Betrand Wettbewerb
Der Betrand Wettbewerb wird auch Preiswettbewerb genannt. Die strategische Variable, über die die Unternehmen ihren Gewinn maximieren ist der Preis (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part \pi_i}{\part p_i}}
).
In der Betrachtung wie Unternehmen ihren Gewinn maximieren musss zwischen differenzierten und homogenen Gütern unterschieden werden.
Homogene Güter
Homogene Güter sind Güter, bei denen Konsumenten keine Präferenzen für eines der Güter haben. Dies unterscheidet sich nur minimal von der Definition der Substitute. Konsumenten sind indifferent zwischen dem Konsum des Gutes von Unternehmen 1 und von Unternehmen 2. Das einzige Entscheidungskriterium ist daher der Preis. Ist das Gut von Unternehmen 1 günstiger als von Unternehmen 2, so kauft der Konsument das Gut von Unternehmen 1 und andersherum. Dies stellt sich als Anreiz für beide Unternehmen dar, sich minimal zu unterbieten und so die gesamte Marktnachfrage auf sich zu ziehen. Solange der Preis überhalb der Grenzkosten liegt nehmen beide Unternehmen an dem Preiwettbewerb teil. Haben beide Unternehmen identische Grenzkosten, stellt sich der Marktpreis bei den Grenzkosten ein. Hat ein Unternehmen etwas höhere Grenzkosten, so liegt der Marktpreis bei den höheren Grenzkosten.
Beispiel: Unternehmen 1 hat Grenzkosten von a und Unternehmen Grenzkosten von b, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a<b }
. Beide Unternehmen können sich so lange Unterbieten, bis der Marktpreis bei b liegt. Unternehmen 2 kann nun nicht mehr unterbieten, da es sonst mit jeder Einheit Verlust macht. Unternehmen bietet einen Preis minimal unterhalb von b an. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P=b-\varepsilon }
, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varepsilon }
gegen 0 strebt, da Unternehmen 1 einen Anreiz hat die Grenzkosten möglichst gering zu unterbieten. Daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{\varepsilon \rightarrow 0}{b-\varepsilon}=b }
.
Differenzierte Güter
Konsumenten haben bei differenzierten Gütern Präferenzen gegenüber den Gütern. In diesem Fall begegnen beide Unternehmen nicht mehr zwangsläufig der selben Nachfrage.
Beispiel: Vielen Nachfragern ist es nicht egal, ob sie Sportsachen von Nike oder von Adidas tragen, einige präferieren Nike und andere Adidas. Die Nachfrage der beiden Konzerne ist nicht vollkommen elastisch. Ihre Nachfrage ist jedoch auch nicht vollkommen unelastisch, denn sollte der Preis von Nike zu groß sein, werden auch die größten Nike Fans irgendwann zu Adidas wechseln. Andersherum steigt die Nachfrage nach Nike Artikeln, wenn Adidas seine Preise anhebt. Die eigene Nachfrage hat also eine negative Relation mit dem eigenen Preis und eine positive mit dem Preis der anderen Unternehmen.
Allgemein gilt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_1=a-bp_1+cp_2}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle q_2=a-bp_2+cp_2}
In dem oben geschilderten Fall wird Symmetrie angenommen, dies muss aber nicht zwangsläufig vorliegen. Symmetrie bedeutet, dass die Nachgefragte Menge von Unternehmen 1 im selben Maß vom eigenen Preis (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1}
) abhängt, wie die Nachfrage von Unternehmen 2 vom eigenen Preis (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_2}
).
Aufgrund der Symmetrie genügt die Betrachtung von Unternehmen 1 um das Verständnis des Preiswettbewerbs mit differenzierten Gütern zu verstehen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_1=p_1*q_1=p_1(a-bp_1+cp_2)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part \pi_1}{\part p_1}=a-2bp_1+cp_2=0}
Umstellen nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1 }
ergibt erneut eine Reaktionsfunktion, die abhängig von dem Preis des anderen Unternehmens ist.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1(p_2)=\frac{a}{2b}+\frac{c}{2b}p_2 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_2(p_1)=\frac{a}{2b}+\frac{c}{2b}p_1 }