Engelkurve: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 28: | Zeile 28: | ||
'''Notwendige Güter''' <br> | '''Notwendige Güter''' <br> | ||
Die Nachfrage nach [[Güterarten|Notwendigen Güter]] muss im steigenden Einkommen langsamer steigen, als das Einkommen. Die Nachfrage nach ihnen steigt unterproportional. Das heißt, dass die Nachfrage immer zunimmt, wenn das Einkommen steigt, jedoch um einen immer kleiner werdenden Wert. <br> | Die Nachfrage nach [[Güterarten|Notwendigen Güter]] muss im steigenden Einkommen langsamer steigen, als das Einkommen. Die Nachfrage nach ihnen steigt unterproportional. Das heißt, dass die Nachfrage immer zunimmt, wenn das Einkommen steigt, jedoch um einen immer kleiner werdenden Wert. <br> | ||
| − | ''Beispiel'': Zucker ist für | + | ''Beispiel'': Zucker ist für Bettina ein notwendiges Gut. Verdoppelt sich das Einkommen von ihr, fragt sie auch mehr Zucker nach, jedoch weniger als doppelt so viel. Bei einem Einkommen von 10 fragt sie beispielsweise 20 Einheiten von Zucker nach und bei einem Einkommen von 20 fragt sie 30 Einheiten nach. <br> |
Es muss gelten: <br> | Es muss gelten: <br> | ||
<math> \frac{\part x(E)}{\part E}>0 </math> <br> | <math> \frac{\part x(E)}{\part E}>0 </math> <br> | ||
und <br> | und <br> | ||
<math> \frac{\part^2 x(E)}{\part^2 E}<0 </math> <br> | <math> \frac{\part^2 x(E)}{\part^2 E}<0 </math> <br> | ||
| − | [[Datei:Engelkurve3.png|350px|rahmenlos]] | + | [[Datei:Engelkurve3.png|350px|rahmenlos]] <br clear=all> |
| + | Es gilt zu beachten, dass die grafische Darstellung der Engelkurve in der <math> E(x) </math>-Form ist, die Ableitungen oben jedoch in der <math> x(E) </math>-Form. Daher ist die grafisch dargestellte Funktion konvex. Beginnend vom Urpsrung die Einkommens-Achse entlang verlaufend steigt auch die Menge von <math> x_1 </math>. Für jede Einheit von E steigt <math> x_1 </math> weniger stark an. Eine inverse Darstellung der Engelkurve würde auch grafisch eine konkave Funktion ergeben, deren zweite Ableitung kleiner als null ist. | ||
| + | <br> | ||
| + | <br> | ||
| + | '''Homothetische Präferenzen''' <br> | ||
| + | Die Nachfrage nach Gütern, die [[Güterarten|Homothetische Präferenzen]] nachweisen, steigt proportional zum Einkommen. Verdoppelt sich das Einkommen/Budget, dann verdoppelt sich auch die nutzenmaximale Menge dieses Gutes. <br> | ||
| + | Es muss gelten: <br> | ||
| + | <math> \frac{\part x(E)}{\part E}>0 </math> <br> | ||
| + | und <br> | ||
| + | <math> \frac{\part^2 x(E)}{\part^2 E}=0 </math> <br> | ||
| + | [[Datei:Engelkurve4.png|350px|rahmenlos]] <br clear=all> | ||
| + | Die Engelkurve ist eine Ursprungsgerade, die eine konstante Steigung aufweist, welche nicht zwingend eins entsprechen muss. | ||
| + | <br> | ||
| + | <br> | ||
| + | Die Nachfrage nach [[Güterarten|Luxusgütern]] steigt bei wachsendem Einkommen stärker an, als das Einkommen selbst. Verdoppelt sich das Budget/Einkommen, ist die nutzenmaximale Nachfrage nach diesem Gut mehr als doppelt so groß. <br> | ||
| + | <math> \frac{\part x(E)}{\part E}>0 </math> <br> | ||
| + | und <br> | ||
| + | <math> \frac{\part^2 x(E)}{\part^2 E}>0 </math> <br> | ||
| + | ''Beispiel'': Für Chrsitian sind Autos Luxusgüter. Er hat ein Auto und nach dem sich sein Einkommen verdoppelt hat, kauft er sich zwei weitere und hat drei Autos. <br> | ||
| + | [[Datei:Engelkurve2.png|350px|rahmenlos]] <br clear=all> | ||
| + | Die Engelkurve hat einen konkaven Verlauf. Ist die zweite Ableitung größer als null, ist die Funktion jedoch konvex. Dies liegt daran, dass die grafische Darstellung in der <math> E(x) </math>-Form ist, jedoch <math> x(E) </math> zweimal nach E differenziert wird. | ||
==MC Fragen== | ==MC Fragen== | ||
Version vom 14. Juli 2023, 16:00 Uhr
Definition
Die Engel-Kurve bildet die Effekte einer Einkommensvariation auf die individuelle Güternachfrage ab, das heißt den Zusammenhang zwischen der Güternachfrage x beziehungsweise y und dem Einkommen E. Sie stellt als Funktion die veränderte nutzenmaximale Nachfrage nach einem Gut bei variierendem Einkommen dar.
Die Engel-Kurve
Das Haushaltsoptimum stellt die optimale Nachfrage nach beiden Gütern da. Bei den Gütern und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
ergeben sich die beiden optimalen Nachfragen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1(p_1,p_2,E) }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2(p_1,p_2,E) }
. Die Nachfrage nach dem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
ist abhängig von den beiden Preisen und dem Einkommen E. Verändert sich das Einkommen E, kann das veränderte Einkommen in die Nachfragefunktion eingesetzt werden und es ergibt sich die neue optimale Nachfrage nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
für das veränderte E. Die Nachfragefunktion lässt sich nach E umstellen, sodass die neue Funktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
und den neuen Preisen abhängig ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E(p_1,p_2,x_1) }
. Diese Funktion gibt an welches Budget E nötig ist um ein bestimmtes Level von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
zu erreichen. Die neue Funktion ist die Funktionsgleichung der Engel-Kurve.
Beispiel: Die Nachfrage nach Pizza (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
) lautet
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1(p_1,p_2,E)=\frac{E+p_2-p_1}{p_1} }
wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
das Gut Döner ist. Die Funktion nach E umgestellt ergibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=p_1x_1-p_2+p_1 }
. Angenommen Pizza kostet 1€ und Döner kostet 1€. Dann lautet die Funktion der Engel-Kurve .
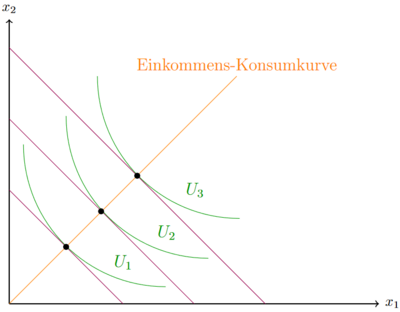
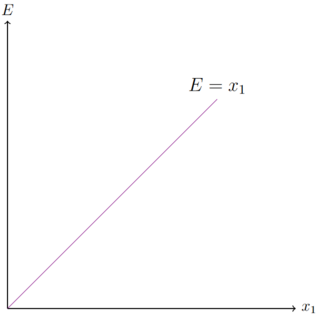
Bei dem vorliegenden Beispiel steigt auch die nutzenmaximale Nachfrage nach dem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
, wenn das Einkommen steigt. Dies ist in der Funktionsgleichung und der Abbildungen der Engelkurve und der Einkommens-Konsumkurve erkennbar.
Inferiore Güter
Die Nachfrage nach Inferioren Gütern sinkt bei steigendem Einkommen. Bei einem steigenden Budget verschiebt sich die Budgetrestriktion und Budgetgerade#Budgetgerade parallel nach Außen. Je weiter die Budgetgerade vom Ursprung entfernt ist, desto größer ist das Budget/Einkommen. Bei Inferioren Gütern muss der Tangentialpunkt einen numerisch immer kleiner werdenden Wert annehmen, als beim nächst kleineren Einkommen.
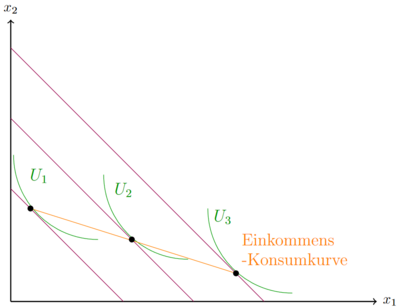
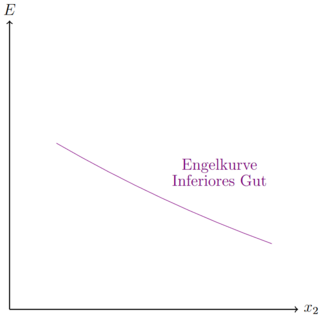
In dem Beispiel oben ist das Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
ein inferiores Gut und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
. Je größer das Budget/Einkommen ist, desto weniger wird nutzenmaximal von nachgefragt. Die Steigung der Engelkurve dieses Gutes ist fallend.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part x(E)}{\part E}<0 }
Normale Güter
Die Nachfrage nach Normalen Gütern steigt bei steigendem Einkommen. Bei ihnen muss der Tangentialpunkt im steigenden Einkommen einen numerisch immer größer werdenden Wert annehmen. Es muss gelten
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part x(E)}{\part E}>0 }
Notwendige Güter
Die Nachfrage nach Notwendigen Güter muss im steigenden Einkommen langsamer steigen, als das Einkommen. Die Nachfrage nach ihnen steigt unterproportional. Das heißt, dass die Nachfrage immer zunimmt, wenn das Einkommen steigt, jedoch um einen immer kleiner werdenden Wert.
Beispiel: Zucker ist für Bettina ein notwendiges Gut. Verdoppelt sich das Einkommen von ihr, fragt sie auch mehr Zucker nach, jedoch weniger als doppelt so viel. Bei einem Einkommen von 10 fragt sie beispielsweise 20 Einheiten von Zucker nach und bei einem Einkommen von 20 fragt sie 30 Einheiten nach.
Es muss gelten:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part x(E)}{\part E}>0 }
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part^2 x(E)}{\part^2 E}<0 }
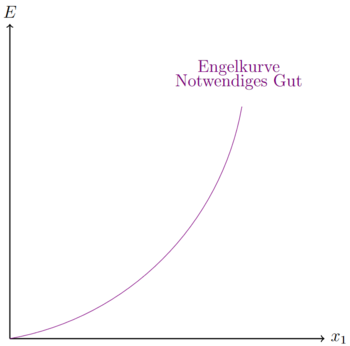
Es gilt zu beachten, dass die grafische Darstellung der Engelkurve in der -Form ist, die Ableitungen oben jedoch in der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x(E) }
-Form. Daher ist die grafisch dargestellte Funktion konvex. Beginnend vom Urpsrung die Einkommens-Achse entlang verlaufend steigt auch die Menge von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
. Für jede Einheit von E steigt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
weniger stark an. Eine inverse Darstellung der Engelkurve würde auch grafisch eine konkave Funktion ergeben, deren zweite Ableitung kleiner als null ist.
Homothetische Präferenzen
Die Nachfrage nach Gütern, die Homothetische Präferenzen nachweisen, steigt proportional zum Einkommen. Verdoppelt sich das Einkommen/Budget, dann verdoppelt sich auch die nutzenmaximale Menge dieses Gutes.
Es muss gelten:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part x(E)}{\part E}>0 }
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part^2 x(E)}{\part^2 E}=0 }
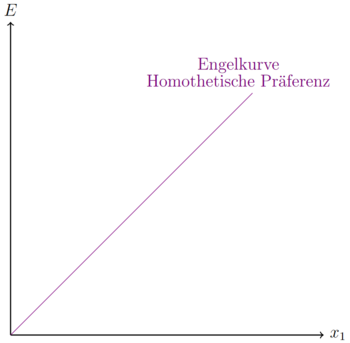
Die Engelkurve ist eine Ursprungsgerade, die eine konstante Steigung aufweist, welche nicht zwingend eins entsprechen muss.
Die Nachfrage nach Luxusgütern steigt bei wachsendem Einkommen stärker an, als das Einkommen selbst. Verdoppelt sich das Budget/Einkommen, ist die nutzenmaximale Nachfrage nach diesem Gut mehr als doppelt so groß.
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part^2 x(E)}{\part^2 E}>0 }
Beispiel: Für Chrsitian sind Autos Luxusgüter. Er hat ein Auto und nach dem sich sein Einkommen verdoppelt hat, kauft er sich zwei weitere und hat drei Autos.
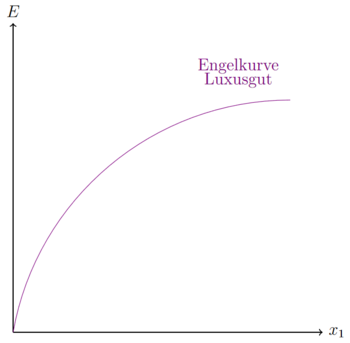
Die Engelkurve hat einen konkaven Verlauf. Ist die zweite Ableitung größer als null, ist die Funktion jedoch konvex. Dies liegt daran, dass die grafische Darstellung in der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E(x) }
-Form ist, jedoch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x(E) }
zweimal nach E differenziert wird.
