Intertemporale Entscheidung: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Die Intertemporale Entscheidung betrachtet die Entscheidungsfindung eines Haushalts zwischen dem Konsum in mehreren Perioden. Für die OMIK dient ein Zwei-Peri…“) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 4: | Zeile 4: | ||
==Intertemporale Nutzenfunktion== | ==Intertemporale Nutzenfunktion== | ||
| + | Der Nutzen des Haushaltes ist von dem Konsumniveau der verschiedenen Perioden abhängig. Im Zwei-Perioden-Modell bedeutet das <math> U(C_0,C_1) </math>. <math> C_0 </math> stellt das Konsumniveau in der derzeitigen Periode dar und <math> C_1 </math> das Konsumniveaus der darauffolgenden Periode. Der Nutzen aus dem Konsum in der späteren Periode wird mit <math> \rho </math> abdiskontiert. Der Diskontfaktor beschreibt die Neigung von Individuen den Nutzen zukünftiger Perioden schwächer zu bewerten, als dern Nutzen heutiger Perioden. Werden Konsumenten gefragt, ob sie lieber heute ein Mittagessen ausgegeben bekommen möchten oder lieber in 30 Jahren, entscheiden sich die meisten für ein heutiges Mittagessen. Der Diskontfaktor ist somit ein Hilfsmittel, um das Modell der Konsumentscheidung in der heutigen Periode realistischer zu gestalten. <br> | ||
| + | <math> U(C_0,C_1)=u(C_0)+\frac{u(C_1)}{1+\rho} </math> ,wobei <math> \rho < 1 </math> <br> | ||
| + | Je größer <math> \rho </math> ist, desto stärker wird die Zukuft abdiskontiert und desto stärker ist die Präferenz für den Gegenwartskonsum. Der [[Marginale Sichtweise|Grenznutzen]] ist positiv und abnehmend. | ||
==Intertemporale Budgetrestriktion== | ==Intertemporale Budgetrestriktion== | ||
| + | Die Intertemporale Budgetrestriktion beinhaltet alle Restriktionen über die verschienen Perioden hinweg. Der Haushalt hat in jeder Periode ein verfügbares Einkommen von <math> M_t </math>.Existiert in dem Intertemporalen Modell ein Kapitalmarkt, hat der Haushalt die Möglichkeit einen Kredit aufzunehmen und damit Konsum in die heutige Periode zu verlagern oder zu sparen und somit einen Teil des Konsums in die nächtse Periode zu verschieben. | ||
| + | <br> | ||
| + | '''Kein Kapitalmarkt''' <br> | ||
| + | Existiert kein Kapitalmarkt, kann der Haushalt nur das Vermögen konsumieren, das er in der jeweiligen Periode zur Verfügung hat. Die Nutzenmaximierung besteht in diesem Fall darin das gesamte Vermögen in der jeweiligen Periode zu konsumieren. Die Budgetrestriktion und Lösung der Maximierungsaufgabe lautet: <br> | ||
| + | <math> C_0^*=M_0 </math> <br> | ||
| + | <math> C_1^*=M_1 </math> <br> | ||
| + | <br> | ||
| + | '''Mit Kapitalmarkt''' <br> | ||
| + | Mit einem Kapitalmarkt hat der Haushalt in der ersten Periode mehr Entscheidungsmöglichkeiten. Neben dem vollständigen Konsum kann er auch einen Teil sparen oder durch einen Kredit Vermögen aus der Zukunft nutzen. Die Ausgaben des Konsums und die Summe, die gespart wird, muss gleich dem verfügbaren Einkommen sein. Spart ein Haushalt, ist die Sparsumme positiv, nimmt er ein Kredit auf, ist die Sparsumme negativ. <br> | ||
| + | '''Periode 0''': <math> Verm \ddot gen=Konsumausgaben+Sparsumme </math> <br> | ||
| + | (i) <math> M_o=p_0C_0+S </math> <br> | ||
| + | In der zweiten Periode bleibt dem Haushalt nur der Konsum des gesamten Vermögens. <br> | ||
| + | '''Periode 1''': <math> Verm \ddot gen+verzinste\,Sparsumme=Konsumausgaben </math> <br> | ||
| + | (ii) <math> M_1+(1+r)S=p_1C_1 </math> <br> | ||
| + | Zur Vereinfachung ist der Preis für ein Konsumgut auf 1 normiert und es existiert keine Inflatio damit <math> p_o=p_1 </math> gilt <br> | ||
| + | (i) nach S umgestellt ergibt <math> S=M_o-C_0 </math> <br> | ||
| + | In (ii) eingesetzt: <br> | ||
| + | <math> M_1+(1+r)(M_0-C_0)=C_1 </math> <br> | ||
| + | <math> M_1+(1+r)M_0=C_1+C_0(1+r) </math> <br> | ||
| + | <math> M_0+\frac{M_1}{1+r}=C_0+\frac{C_1}{1+r} </math> <br> | ||
| + | Das mit dem Zinssatz auf die heutige Periode abdiskontierte Vermögen aller Perioden muss gleich den mit dem Zinssatz auf die heutige Periode abdiskontierten Konsumausgaben sein. Oder anders formuliert: Der Present Value des Vermögens entspricht dem Present Value der Konsumausgaben. <br> | ||
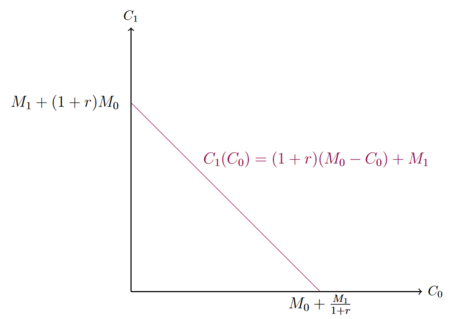
| + | Für eine grafische Darstellung der Budgetgeraden muss nach <math> C_0 </math> oder <math> C_1 </math> umgestellt werden. <br> | ||
| + | [[Datei:InterBudget.png|450px|rahmenlos]] <br clear=all> | ||
| + | Die Budgetrestriktion gilt für alle <math> r \geq </math>. <br> | ||
| + | Steigt <math> M_0 </math> oder <math> M_1 </math>, verschiebt sich die Budgetgerade nach außen. Bei <math> r=0 </math> verschiebt sie sich parrallel. Steigt der Zinssatz <math> r </math>, wird die Budgetgerade steiler. | ||
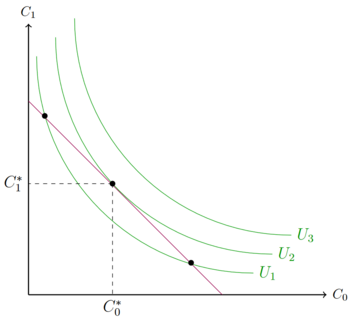
==Intertemporale Nutzenmaximierung== | ==Intertemporale Nutzenmaximierung== | ||
| + | [[Datei:InterHaushaltsoptimum.png|350px|rahmenlos]] | ||
==MC Fragen== | ==MC Fragen== | ||
Version vom 24. Juli 2023, 10:20 Uhr
Die Intertemporale Entscheidung betrachtet die Entscheidungsfindung eines Haushalts zwischen dem Konsum in mehreren Perioden. Für die OMIK dient ein Zwei-Perioden Modell, in dem in beiden Perioden jeweils ein Budget Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M } zur Verfügung steht.
Intertemporale Nutzenfunktion
Der Nutzen des Haushaltes ist von dem Konsumniveau der verschiedenen Perioden abhängig. Im Zwei-Perioden-Modell bedeutet das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(C_0,C_1) }
. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_0 }
stellt das Konsumniveau in der derzeitigen Periode dar und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_1 }
das Konsumniveaus der darauffolgenden Periode. Der Nutzen aus dem Konsum in der späteren Periode wird mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho }
abdiskontiert. Der Diskontfaktor beschreibt die Neigung von Individuen den Nutzen zukünftiger Perioden schwächer zu bewerten, als dern Nutzen heutiger Perioden. Werden Konsumenten gefragt, ob sie lieber heute ein Mittagessen ausgegeben bekommen möchten oder lieber in 30 Jahren, entscheiden sich die meisten für ein heutiges Mittagessen. Der Diskontfaktor ist somit ein Hilfsmittel, um das Modell der Konsumentscheidung in der heutigen Periode realistischer zu gestalten.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(C_0,C_1)=u(C_0)+\frac{u(C_1)}{1+\rho} }
,wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho < 1 }
Je größer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho }
ist, desto stärker wird die Zukuft abdiskontiert und desto stärker ist die Präferenz für den Gegenwartskonsum. Der Grenznutzen ist positiv und abnehmend.
Intertemporale Budgetrestriktion
Die Intertemporale Budgetrestriktion beinhaltet alle Restriktionen über die verschienen Perioden hinweg. Der Haushalt hat in jeder Periode ein verfügbares Einkommen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_t }
.Existiert in dem Intertemporalen Modell ein Kapitalmarkt, hat der Haushalt die Möglichkeit einen Kredit aufzunehmen und damit Konsum in die heutige Periode zu verlagern oder zu sparen und somit einen Teil des Konsums in die nächtse Periode zu verschieben.
Kein Kapitalmarkt
Existiert kein Kapitalmarkt, kann der Haushalt nur das Vermögen konsumieren, das er in der jeweiligen Periode zur Verfügung hat. Die Nutzenmaximierung besteht in diesem Fall darin das gesamte Vermögen in der jeweiligen Periode zu konsumieren. Die Budgetrestriktion und Lösung der Maximierungsaufgabe lautet:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_0^*=M_0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_1^*=M_1 }
Mit Kapitalmarkt
Mit einem Kapitalmarkt hat der Haushalt in der ersten Periode mehr Entscheidungsmöglichkeiten. Neben dem vollständigen Konsum kann er auch einen Teil sparen oder durch einen Kredit Vermögen aus der Zukunft nutzen. Die Ausgaben des Konsums und die Summe, die gespart wird, muss gleich dem verfügbaren Einkommen sein. Spart ein Haushalt, ist die Sparsumme positiv, nimmt er ein Kredit auf, ist die Sparsumme negativ.
Periode 0: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Verm \ddot gen=Konsumausgaben+Sparsumme }
(i) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_o=p_0C_0+S }
In der zweiten Periode bleibt dem Haushalt nur der Konsum des gesamten Vermögens.
Periode 1: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Verm \ddot gen+verzinste\,Sparsumme=Konsumausgaben }
(ii) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_1+(1+r)S=p_1C_1 }
Zur Vereinfachung ist der Preis für ein Konsumgut auf 1 normiert und es existiert keine Inflatio damit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_o=p_1 }
gilt
(i) nach S umgestellt ergibt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=M_o-C_0 }
In (ii) eingesetzt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_1+(1+r)(M_0-C_0)=C_1 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_1+(1+r)M_0=C_1+C_0(1+r) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_0+\frac{M_1}{1+r}=C_0+\frac{C_1}{1+r} }
Das mit dem Zinssatz auf die heutige Periode abdiskontierte Vermögen aller Perioden muss gleich den mit dem Zinssatz auf die heutige Periode abdiskontierten Konsumausgaben sein. Oder anders formuliert: Der Present Value des Vermögens entspricht dem Present Value der Konsumausgaben.
Für eine grafische Darstellung der Budgetgeraden muss nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_0 }
oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_1 }
umgestellt werden.
Die Budgetrestriktion gilt für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r \geq }
.
Steigt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_0 }
oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_1 }
, verschiebt sich die Budgetgerade nach außen. Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=0 }
verschiebt sie sich parrallel. Steigt der Zinssatz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r }
, wird die Budgetgerade steiler.