Präferenzenarten: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
|||
| (12 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Präferenzen von Konsumenten bestimmen, wie sie Güter wahrnehmen. Die Präferenzenart eines Gutes steht immer in Verbindung eines anderen Gutes. Ein Gut <math> x_1 </math> kann beispielsweise ein Substitut für ein Gut <math> x_2 </math> sein und gleichzeitig ein Komplement für ein anderes Gut <math> x_3 </math>. | + | Präferenzen von Konsumenten bestimmen, wie sie mehrere Güter wahrnehmen. Die Präferenzenart eines Gutes steht immer in Verbindung eines anderen Gutes. Ein Gut <math> x_1 </math> kann beispielsweise ein Substitut für ein Gut <math> x_2 </math> sein und gleichzeitig ein Komplement für ein anderes Gut <math> x_3 sein. </math>. |
__TOC__ | __TOC__ | ||
| Zeile 5: | Zeile 5: | ||
==Substitute== | ==Substitute== | ||
Substitute sind Güter, bei denen die Erhöhung des Preises eines Gutes zu einer Erhöhung der nachgefragten Menge des anderen Gutes führt. Die [[Elastizitäten#Kreuzpreiselastizität|Kreuzpreiselastizität]] ist bei Substituten positiv. Dies bedeutet, dass die Nachfrage nach einem Gut <math> x_1 </math> steigt, wenn der Preis eines anderen Gutes <math> x_2 </math> steigt.<br> | Substitute sind Güter, bei denen die Erhöhung des Preises eines Gutes zu einer Erhöhung der nachgefragten Menge des anderen Gutes führt. Die [[Elastizitäten#Kreuzpreiselastizität|Kreuzpreiselastizität]] ist bei Substituten positiv. Dies bedeutet, dass die Nachfrage nach einem Gut <math> x_1 </math> steigt, wenn der Preis eines anderen Gutes <math> x_2 </math> steigt.<br> | ||
| − | ''Beispiel'': Sebastian steht im Supermarkt immer vor der Wahl zwischen Margarine und Butter. Eigentlich mag er Butter mehr, deshalb kauft er im Jahr insgesamt 10 Packungen Butter und 2 Packungen Margarine. Da sich die Produktionskosten von Butter erhöhen, steigt auch der Preis von Butter. Sebastian mag Butter zwar lieber, jedoch geht es ihm nur darum einen Streichfett für seinen leckeren Brotbelag zu finden. Daher bewegt ihn die Preiserhöhung dazu etwas weniger Butter und etwas mehr Margarine zu kaufen. Sebastian ist bereit das eine Gut durch das andere Gut zu substituieren. <br> | + | ''Beispiel'': Sebastian steht im Supermarkt immer vor der Wahl zwischen Margarine und Butter. Eigentlich mag er Butter mehr, deshalb kauft er im Jahr insgesamt 10 Packungen Butter und 2 Packungen Margarine. Da sich die Produktionskosten von Butter erhöhen, steigt auch der Preis von Butter. Sebastian mag Butter zwar lieber, jedoch geht es ihm nur darum einen Streichfett für seinen leckeren Brotbelag zu finden. Daher bewegt ihn die Preiserhöhung dazu etwas weniger Butter und etwas mehr Margarine zu kaufen. Sebastian ist bereit das eine Gut durch das andere Gut zu ersetzen (substituieren). <br> |
[[Datei:Substitute.png|350px|rahmenlos]] | [[Datei:Substitute.png|350px|rahmenlos]] | ||
<br> | <br> | ||
| Zeile 13: | Zeile 13: | ||
'''Perfekte Substitute''' <br> | '''Perfekte Substitute''' <br> | ||
| − | Perfekte Substitute zeichnen sich dadurch aus, dass ein Gut durch das andere Gut vollständig substituiert werden kann. Es ist somit | + | Perfekte Substitute zeichnen sich dadurch aus, dass ein Gut durch das andere Gut vollständig substituiert werden kann. Es ist somit möglich gar nichts von einem der Güter zu konsumieren. Hierbei ist das Verhältnis, zu dem das eine Gut mit dem anderen Gut substituiert wird, ohne Nutzen zu verlieren, konstant. Die [[Präferenzen und Indifferenzkurven|Indifferenzkurve]] ist bei perfekten Substituten eine Gerade. Dies liegt daran, dass die [[Präferenzen und Indifferenzkurven#Die Steigung der Indifferenzkurve bzw. Grenzrate der Substitution|Grenzrate der Substitution]] des einen Guts durch das andere Gut konstant ist. <br> |
''Erstes Beispiel'': Ein Konsument ist unabhängig vom Konsumniveau immer indifferent zwischen einer Packung Salzstangen und zwei Packungen Gummibärchen. Der Konsument wäre also immer bereit eine Packung Salzstangen abzugeben, sollte er im Gegenzug zwei Packungen Gummibärchen bekommen. Und da er bereit ist dies unabhängig vom aktuellen Konsumniveau, also unbeachtet dessen wie viele Einheiten er der beiden Güter bereits konsumiert, ist die Indifferenzkurve eine Gerade. <br> | ''Erstes Beispiel'': Ein Konsument ist unabhängig vom Konsumniveau immer indifferent zwischen einer Packung Salzstangen und zwei Packungen Gummibärchen. Der Konsument wäre also immer bereit eine Packung Salzstangen abzugeben, sollte er im Gegenzug zwei Packungen Gummibärchen bekommen. Und da er bereit ist dies unabhängig vom aktuellen Konsumniveau, also unbeachtet dessen wie viele Einheiten er der beiden Güter bereits konsumiert, ist die Indifferenzkurve eine Gerade. <br> | ||
''Zweites Beispiel'': Mirko kann nur zwei Güter im Kino konsumieren: Nachos und/oder Popcorn. Mirko schmeckt beides gleich gut und er wird von beiden Snacks gleichmäßig gesättigt. Ihm wäre es egal, wenn er eine Portion Popcorn für eine Portion Nachos eintauschen müsste. Seine Nutzenfunktion der beiden Snacks sei in <math> U(x_1,x_2)=x_1+x_2 </math> beschrieben. Umgeschrieben ergibt sich folgende Funktion für eine Nutzenfunktion mit einem konstanten Nutzenniveau:<br> | ''Zweites Beispiel'': Mirko kann nur zwei Güter im Kino konsumieren: Nachos und/oder Popcorn. Mirko schmeckt beides gleich gut und er wird von beiden Snacks gleichmäßig gesättigt. Ihm wäre es egal, wenn er eine Portion Popcorn für eine Portion Nachos eintauschen müsste. Seine Nutzenfunktion der beiden Snacks sei in <math> U(x_1,x_2)=x_1+x_2 </math> beschrieben. Umgeschrieben ergibt sich folgende Funktion für eine Nutzenfunktion mit einem konstanten Nutzenniveau:<br> | ||
<math> x_2=\bar{U}-x_1 </math> <br> | <math> x_2=\bar{U}-x_1 </math> <br> | ||
| − | Die Indifferenzkurve hat eine Steigung von -1. | + | Die Indifferenzkurve hat eine Steigung von -1. Typisch für die Nutzenfunktion von Perfekten Substituten ist das Vorliegen von Achsenabschnitten.<br> |
[[Datei:Perfekte Substitute.png|351px|rahmenlos]] | [[Datei:Perfekte Substitute.png|351px|rahmenlos]] | ||
<br> | <br> | ||
| Zeile 25: | Zeile 25: | ||
<br> | <br> | ||
'''Imperfekte Substitute''' <br> | '''Imperfekte Substitute''' <br> | ||
| − | Imperfekte Substitute (auch unvollkommene Substitute) zeichnen sich | + | Imperfekte Substitute (auch unvollkommene Substitute) zeichnen sich dadurch aus, dass sie durch andere Güter austauschbar sind (substituierbar), jedoch nicht vollends auf eins der beiden Güter für ein Nutzenniveau größer null verzichtet werden kann. Die [[Präferenzen und Indifferenzkurven#Indifferenzkurven|Indifferenzkurven]] der Imperfekten Substitute schneiden/berühren daher nie die Achsen. <br> |
| − | ''Beispiel'': Tom möchte einen Auflauf machen. Hierbei muss er sich für ein Verhältnis zwischen Bohnen und Nudeln entscheiden. Alle anderen Zutaten sind mit festen Maßeinheiten in dem Rezept festgeschrieben. Tom benötigt sowohl | + | ''Beispiel'': Tom möchte einen Auflauf machen. Hierbei muss er sich für ein Verhältnis zwischen Bohnen und Nudeln entscheiden. Alle anderen Zutaten sind mit festen Maßeinheiten in dem Rezept festgeschrieben. Tom benötigt sowohl das Eiweiß der Bohnen, als auch die Kohlenhydrate der Nudeln, weshalb er auf keiner der beiden Zutaten vollständig verzichten kann. Abgetragen auf ein Kartoffel-Bohnen-Diagramm bedeutet dies, dass die Indifferenzkurven niemals die Achsen schneiden. Je weniger Tom von einem der beiden Gütern hat, desto mehr benötigt er von dem anderen, damit er weiterhin den selben Nutzen erhält. Eine mögliche Indifferenzkurve sieht wie folgt aus: <br> |
[[Datei:ImperfekteSubstitute.png|350px|rahmenlos]] <br> | [[Datei:ImperfekteSubstitute.png|350px|rahmenlos]] <br> | ||
<br clear=all> | <br clear=all> | ||
| Zeile 32: | Zeile 32: | ||
==Perfekte Komplemente== | ==Perfekte Komplemente== | ||
| − | Perfekte Komplementärgüter müssen in einem festen Verhältnis miteinander konsumiert werden (sie verhalten sich komplementär zueinander). Die [[Präferenzen und Indifferenzkurven#Die Steigung der Indifferenzkurve bzw. Grenzrate der Substitution|Grenzrate der Substitution]] bei Perfekten Komplementen ist unendlich. Das bedeutet, dass die Nachfrage nach einem Gut <math> x_1 </math> sinkt, wenn der Preis eines Gutes <math> x_2 </math> steigt. Daher ist die [[Elastizitäten#Kreuzpreiselastizität|Kreuzpreiselastizität]] negativ. Da die Güter in einem festen Verhältnis konsumiert werden müssen, erhöht der gesteigerte Konsum eines | + | Perfekte Komplementärgüter müssen in einem festen Verhältnis miteinander konsumiert werden (sie verhalten sich komplementär zueinander). Die [[Präferenzen und Indifferenzkurven#Die Steigung der Indifferenzkurve bzw. Grenzrate der Substitution|Grenzrate der Substitution]] bei Perfekten Komplementen ist unendlich. Das bedeutet, dass die Nachfrage nach einem Gut <math> x_1 </math> sinkt, wenn der Preis eines Gutes <math> x_2 </math> steigt. Daher ist die [[Elastizitäten#Kreuzpreiselastizität|Kreuzpreiselastizität]] negativ. Da die Güter in einem festen Verhältnis konsumiert werden müssen, erhöht der gesteigerte Konsum eines Gutes alleine nicht das Nutzenniveau und die [[Präferenzen und Indifferenzkurven#Indifferenzkurven|Indifferenzkurven]] verlaufen in einem rechten Winkel. <br> |
| − | ''Beispiel'': Maria trinkt in ihrer Mittagspause vom Mikro Lernen in der BRuW immer Kaffee. Hierbei mischt sie immer einen Kaffee (<math> x_1 </math>) mit zwei | + | ''Beispiel'': Maria trinkt in ihrer Mittagspause vom Mikro Lernen in der BRuW immer Kaffee. Hierbei mischt sie immer einen Kaffee (<math> x_1 </math>) mit zwei Schlucken Milch (<math> x_2 </math>), da er ihr sonst zu stark ist und nicht schmeckt. Jeder weitere Schluck Milch bringt ihr nicht viel, schadet aber auch nicht ihrem Nutzen. Kauft sie zwei Kaffee und hat nur zwei Schlucke Milch übrig, kann sie nur einen der beiden Kaffee trinken. Erst wenn sie zwei weitere Schlucke Milch hat, stiftet der zweite Kaffee Nutzen. Die Nutzenfunktion kann wie folgt aussehen: <math> U(x_1,x_2)=min\{x_1;0,5x_2\} </math>. Es braucht doppelt so viele Schlucke Milch (<math> x_2 </math>) als Kaffee (<math> x_1 </math>), um auf ein Nutzenniveau höher zu kommen. Das Minimum der beiden bestimmt das Nutzenniveau. Aufgrund der [[Ordinale und Kardinale Nutzentheorie#Ordinale Nutzentheorie|Ordinalen Nutzentheorie]] kann jedoch auch jede monotone Transformation dieselben Präferenzen widerspiegeln. Zum Beispiel <math> \tilde{U}(x_1,x_2)=min\{2x_1;x_2\} </math>). Weitere klassische Beispiele sind: Schuhe, Handschuhe oder Socken. Diese Güter werden immer paarweise konsumiert.<br> |
[[Datei:Perfekte Komplemente.png|351px|rahmenlos]] | [[Datei:Perfekte Komplemente.png|351px|rahmenlos]] | ||
| Zeile 43: | Zeile 43: | ||
+ ...Perfekte Komplemente. | + ...Perfekte Komplemente. | ||
- ...Unvollkommene Substitute. | - ...Unvollkommene Substitute. | ||
| − | - | + | - nicht aus der Aufgabenstellung deutlich identifizierbar |
</quiz> | </quiz> | ||
<quiz display=simple shuffleanswers=true> | <quiz display=simple shuffleanswers=true> | ||
| − | {Christine trinkt gerne | + | {Christine trinkt gerne Koffeinhaltige Getränke und kauft dabei von Cola und Mate das Gut, das im Angebot und damit günstiger als das andere ist. Für Christine sind Cola und Mate... |
|type="()"} | |type="()"} | ||
+ ...Perfekte Substitute. | + ...Perfekte Substitute. | ||
- ...Perfekte Komplemente. | - ...Perfekte Komplemente. | ||
- ...Unvollkommene Substitute. | - ...Unvollkommene Substitute. | ||
| − | - | + | - nicht aus der Aufgabenstellung deutlich identifizierbar |
</quiz> | </quiz> | ||
Aktuelle Version vom 11. August 2023, 14:04 Uhr
Präferenzen von Konsumenten bestimmen, wie sie mehrere Güter wahrnehmen. Die Präferenzenart eines Gutes steht immer in Verbindung eines anderen Gutes. Ein Gut kann beispielsweise ein Substitut für ein Gut sein und gleichzeitig ein Komplement für ein anderes Gut .
Substitute
Substitute sind Güter, bei denen die Erhöhung des Preises eines Gutes zu einer Erhöhung der nachgefragten Menge des anderen Gutes führt. Die Kreuzpreiselastizität ist bei Substituten positiv. Dies bedeutet, dass die Nachfrage nach einem Gut steigt, wenn der Preis eines anderen Gutes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
steigt.
Beispiel: Sebastian steht im Supermarkt immer vor der Wahl zwischen Margarine und Butter. Eigentlich mag er Butter mehr, deshalb kauft er im Jahr insgesamt 10 Packungen Butter und 2 Packungen Margarine. Da sich die Produktionskosten von Butter erhöhen, steigt auch der Preis von Butter. Sebastian mag Butter zwar lieber, jedoch geht es ihm nur darum einen Streichfett für seinen leckeren Brotbelag zu finden. Daher bewegt ihn die Preiserhöhung dazu etwas weniger Butter und etwas mehr Margarine zu kaufen. Sebastian ist bereit das eine Gut durch das andere Gut zu ersetzen (substituieren).
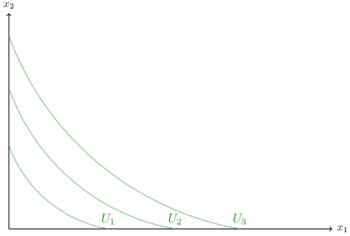
Die Indifferenzkurve von Substituten verläuft fallend.
Perfekte Substitute
Perfekte Substitute zeichnen sich dadurch aus, dass ein Gut durch das andere Gut vollständig substituiert werden kann. Es ist somit möglich gar nichts von einem der Güter zu konsumieren. Hierbei ist das Verhältnis, zu dem das eine Gut mit dem anderen Gut substituiert wird, ohne Nutzen zu verlieren, konstant. Die Indifferenzkurve ist bei perfekten Substituten eine Gerade. Dies liegt daran, dass die Grenzrate der Substitution des einen Guts durch das andere Gut konstant ist.
Erstes Beispiel: Ein Konsument ist unabhängig vom Konsumniveau immer indifferent zwischen einer Packung Salzstangen und zwei Packungen Gummibärchen. Der Konsument wäre also immer bereit eine Packung Salzstangen abzugeben, sollte er im Gegenzug zwei Packungen Gummibärchen bekommen. Und da er bereit ist dies unabhängig vom aktuellen Konsumniveau, also unbeachtet dessen wie viele Einheiten er der beiden Güter bereits konsumiert, ist die Indifferenzkurve eine Gerade.
Zweites Beispiel: Mirko kann nur zwei Güter im Kino konsumieren: Nachos und/oder Popcorn. Mirko schmeckt beides gleich gut und er wird von beiden Snacks gleichmäßig gesättigt. Ihm wäre es egal, wenn er eine Portion Popcorn für eine Portion Nachos eintauschen müsste. Seine Nutzenfunktion der beiden Snacks sei in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(x_1,x_2)=x_1+x_2 }
beschrieben. Umgeschrieben ergibt sich folgende Funktion für eine Nutzenfunktion mit einem konstanten Nutzenniveau:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2=\bar{U}-x_1 }
Die Indifferenzkurve hat eine Steigung von -1. Typisch für die Nutzenfunktion von Perfekten Substituten ist das Vorliegen von Achsenabschnitten.
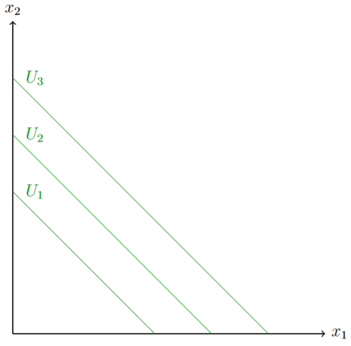
Sind zwei Güter Perfekte Substitute und ihre Preise unterscheiden sich, so kauft ein rational agierender Konsument nur Güter des günstigeren Gutes.
Imperfekte Substitute
Imperfekte Substitute (auch unvollkommene Substitute) zeichnen sich dadurch aus, dass sie durch andere Güter austauschbar sind (substituierbar), jedoch nicht vollends auf eins der beiden Güter für ein Nutzenniveau größer null verzichtet werden kann. Die Indifferenzkurven der Imperfekten Substitute schneiden/berühren daher nie die Achsen.
Beispiel: Tom möchte einen Auflauf machen. Hierbei muss er sich für ein Verhältnis zwischen Bohnen und Nudeln entscheiden. Alle anderen Zutaten sind mit festen Maßeinheiten in dem Rezept festgeschrieben. Tom benötigt sowohl das Eiweiß der Bohnen, als auch die Kohlenhydrate der Nudeln, weshalb er auf keiner der beiden Zutaten vollständig verzichten kann. Abgetragen auf ein Kartoffel-Bohnen-Diagramm bedeutet dies, dass die Indifferenzkurven niemals die Achsen schneiden. Je weniger Tom von einem der beiden Gütern hat, desto mehr benötigt er von dem anderen, damit er weiterhin den selben Nutzen erhält. Eine mögliche Indifferenzkurve sieht wie folgt aus:
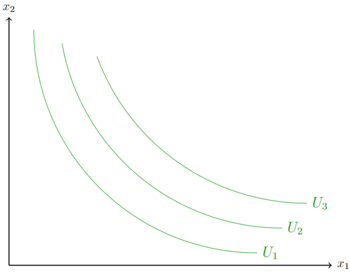
Die Nutzenfunktion von Imperfekten Substituten ist beispielsweise eine Cobb-Douglas-Nutzenfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(x_1,x_2)=x_1^{\alpha}x_2^{\beta} }
.
Perfekte Komplemente
Perfekte Komplementärgüter müssen in einem festen Verhältnis miteinander konsumiert werden (sie verhalten sich komplementär zueinander). Die Grenzrate der Substitution bei Perfekten Komplementen ist unendlich. Das bedeutet, dass die Nachfrage nach einem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
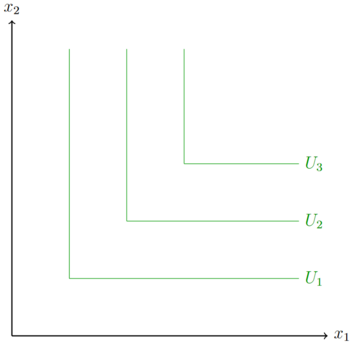
sinkt, wenn der Preis eines Gutes steigt. Daher ist die Kreuzpreiselastizität negativ. Da die Güter in einem festen Verhältnis konsumiert werden müssen, erhöht der gesteigerte Konsum eines Gutes alleine nicht das Nutzenniveau und die Indifferenzkurven verlaufen in einem rechten Winkel.
Beispiel: Maria trinkt in ihrer Mittagspause vom Mikro Lernen in der BRuW immer Kaffee. Hierbei mischt sie immer einen Kaffee (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
) mit zwei Schlucken Milch (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
), da er ihr sonst zu stark ist und nicht schmeckt. Jeder weitere Schluck Milch bringt ihr nicht viel, schadet aber auch nicht ihrem Nutzen. Kauft sie zwei Kaffee und hat nur zwei Schlucke Milch übrig, kann sie nur einen der beiden Kaffee trinken. Erst wenn sie zwei weitere Schlucke Milch hat, stiftet der zweite Kaffee Nutzen. Die Nutzenfunktion kann wie folgt aussehen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(x_1,x_2)=min\{x_1;0,5x_2\} }
. Es braucht doppelt so viele Schlucke Milch (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
) als Kaffee (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
), um auf ein Nutzenniveau höher zu kommen. Das Minimum der beiden bestimmt das Nutzenniveau. Aufgrund der Ordinalen Nutzentheorie kann jedoch auch jede monotone Transformation dieselben Präferenzen widerspiegeln. Zum Beispiel ). Weitere klassische Beispiele sind: Schuhe, Handschuhe oder Socken. Diese Güter werden immer paarweise konsumiert.
MC Fragen
