Cobb-Douglas-Funktionen: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Cobb-Douglas-Funktionen sind Funktionen, die häufig als Nutzenfunktionen oder Produktionsfunktionen genutzt werden. __TOC__ ==Aufbau der Cobb-Douglas-Funkti…“) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 7: | Zeile 7: | ||
<math> z(x_1,...,x_n)=b\prod\limits_{i = 0}^{n}x_i^{\alpha_i} </math> mit <math> b>0 </math> <br> | <math> z(x_1,...,x_n)=b\prod\limits_{i = 0}^{n}x_i^{\alpha_i} </math> mit <math> b>0 </math> <br> | ||
Für die Anwendung in der OMIK genügen zwei Variablen. Zudem kann Parameter <math> b </math> auch den Wert 1 annehmen, sodass sich <math> z(x_1,x_2)=x_1^{\alpha}x_2^{\beta} </math> ergibt. Dies kann dreidimensional dargestellt werden. <br> | Für die Anwendung in der OMIK genügen zwei Variablen. Zudem kann Parameter <math> b </math> auch den Wert 1 annehmen, sodass sich <math> z(x_1,x_2)=x_1^{\alpha}x_2^{\beta} </math> ergibt. Dies kann dreidimensional dargestellt werden. <br> | ||
| − | Datei:CobbDouglas.png|300px|rahmenlos <br clear=all> | + | [[Datei:CobbDouglas.png|300px|rahmenlos]] <br clear=all> |
Charakterlich ist vorallem, dass die Variablen <math> x_1 </math> und <math> x_2 </math> miteinander multipliziert werden. Nimmt einer der beiden Werte null an, ist der z Wert null. | Charakterlich ist vorallem, dass die Variablen <math> x_1 </math> und <math> x_2 </math> miteinander multipliziert werden. Nimmt einer der beiden Werte null an, ist der z Wert null. | ||
==Cobb-Douglas-Nutzenfunktion== | ==Cobb-Douglas-Nutzenfunktion== | ||
| + | |||
==Cobb-Douglas-Produktionsfunktion== | ==Cobb-Douglas-Produktionsfunktion== | ||
==MC Fragen== | ==MC Fragen== | ||
Version vom 17. August 2023, 15:40 Uhr
Cobb-Douglas-Funktionen sind Funktionen, die häufig als Nutzenfunktionen oder Produktionsfunktionen genutzt werden.
Aufbau der Cobb-Douglas-Funktionen
Cobb-Douglas-Funktionen haben einen typischen Aufbau, bei dem Variablen multiplikativ miteinander verknüpft sind und einen Exponenten haben.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z(x_1,...,x_n)=b\prod\limits_{i = 0}^{n}x_i^{\alpha_i} }
mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b>0 }
Für die Anwendung in der OMIK genügen zwei Variablen. Zudem kann Parameter auch den Wert 1 annehmen, sodass sich ergibt. Dies kann dreidimensional dargestellt werden.
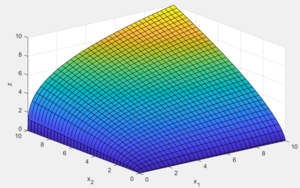
Charakterlich ist vorallem, dass die Variablen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
miteinander multipliziert werden. Nimmt einer der beiden Werte null an, ist der z Wert null.
