Marginale Sichtweise: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 8: | Zeile 8: | ||
==Grenznutzen== | ==Grenznutzen== | ||
| − | Der Grenznutzen | + | Der Grenznutzen (GU oder MU)untersucht, wie sich der Nutzen verhält, wenn das Konsumniveau marginal erhöht wird. In der Theorie wird von einem abnehmenden Grenznutzen ausgegangen. <br> |
''Beispiel'': Nach dem erfolgreichen Bachelor beschließt Tom bei einer Bank fest einzusteigen. Er besitzt keinen Anzug und geht deshalb einkaufen. Er kauft einen ersten Anzug, ohne den er fast gar nicht arbeiten könnte. Der Nutzen, den der erste Anzug stiftet ist sehr groß. Tom kauft einen zweiten Anzug, falls der erste dreckig wird. Auch der zweite Anzug stiftet einen großen Anzug, jedoch einen nicht so großen, wie der erste. Je mehr Anzüge Tom kauft, desto größer wird sein Nutzen. Jeder einzelne Anzug stiftet jedoch einen imemr kleiner werdenden zusätzlichen Nutzen. Der Nutzen einer marginalen Einheit mehr ist positiv, wird aber immer kleiner. <br> | ''Beispiel'': Nach dem erfolgreichen Bachelor beschließt Tom bei einer Bank fest einzusteigen. Er besitzt keinen Anzug und geht deshalb einkaufen. Er kauft einen ersten Anzug, ohne den er fast gar nicht arbeiten könnte. Der Nutzen, den der erste Anzug stiftet ist sehr groß. Tom kauft einen zweiten Anzug, falls der erste dreckig wird. Auch der zweite Anzug stiftet einen großen Anzug, jedoch einen nicht so großen, wie der erste. Je mehr Anzüge Tom kauft, desto größer wird sein Nutzen. Jeder einzelne Anzug stiftet jedoch einen imemr kleiner werdenden zusätzlichen Nutzen. Der Nutzen einer marginalen Einheit mehr ist positiv, wird aber immer kleiner. <br> | ||
| − | + | Der Grenznutzen lässt sich durch die Ableitung der Nutzenfunktion berechnen: <math> MU=\frac{\part U(x)}{\part x} </math> <br> | |
| + | [[Datei:AbnehmenderGrenznutzen.png|350px|rahmenlos]] | ||
| + | [[Datei:MU.png|360px|rahmenlos]] | ||
| + | <br clear=all> | ||
| + | In den Abbildungen oben wird der Bezug zwischen der Grenznutzenfunktion (MU(x)) und der Nutzenfunktion (U(x)) deutlich. Die marginale Steigung in einem Punkt entspricht dem Grenznutzen in diesem Punkt. Grundsätzlich ist es auch möglich einen steigenden Grenznutzen darzustellen. In diesem Fall wäre die Nutzenfunktion [[Mathematische Eigenschaften von Funktionen|konvex]] und nicht [[Mathematische Eigenschaften von Funktionen|konkav]], wie oben dargestellt. | ||
==Grenzkosten== | ==Grenzkosten== | ||
Version vom 22. August 2023, 10:43 Uhr
Definition
Die Marginalanalyse untersucht in der Volkswirtschaftslehre, welchen Effekt eine geringfügige Änderung einer Variablen auf eine oder mehrere andere Variablen hat.
Marginale Sichtweise
In der Volskwirtschaftslehre und insbesonder der Mikroökonomie ist häufig von einem marginalen Effekt die Rede. Dieser marginale Effekt betrachtet, wie sich was verändert, wenn eine Variable sehr gering, also marginal, erhöht wird. Häufig wird untersucht, wie sich zum Beispiel die Kosten verändern, wenn eine Einheit mehr produziert wird. Dies ist in den Anwendungen häufig auch korrekt. Viel genauer wäre es allerdings, wenn bei marginalen Veränderungen von Veränderungen in einem Punkt gesprochen wird. Der marginale Effekt lässt sich durch die Ableitung nach der zu betrachtenden Variable berechnen. Die erste Ableitung einer Funktion gibt die Steigung in dem Punkt des x-Wertes an. Genauso gibt die Ableitung, beispielsweise der Nutzenfunktion an, wie sich der Nutzen marginal in diesem Punkt verändert.
Grenznutzen
Der Grenznutzen (GU oder MU)untersucht, wie sich der Nutzen verhält, wenn das Konsumniveau marginal erhöht wird. In der Theorie wird von einem abnehmenden Grenznutzen ausgegangen.
Beispiel: Nach dem erfolgreichen Bachelor beschließt Tom bei einer Bank fest einzusteigen. Er besitzt keinen Anzug und geht deshalb einkaufen. Er kauft einen ersten Anzug, ohne den er fast gar nicht arbeiten könnte. Der Nutzen, den der erste Anzug stiftet ist sehr groß. Tom kauft einen zweiten Anzug, falls der erste dreckig wird. Auch der zweite Anzug stiftet einen großen Anzug, jedoch einen nicht so großen, wie der erste. Je mehr Anzüge Tom kauft, desto größer wird sein Nutzen. Jeder einzelne Anzug stiftet jedoch einen imemr kleiner werdenden zusätzlichen Nutzen. Der Nutzen einer marginalen Einheit mehr ist positiv, wird aber immer kleiner.
Der Grenznutzen lässt sich durch die Ableitung der Nutzenfunktion berechnen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle MU=\frac{\part U(x)}{\part x} }
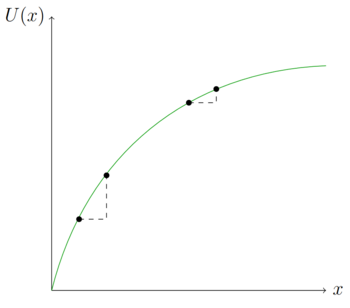
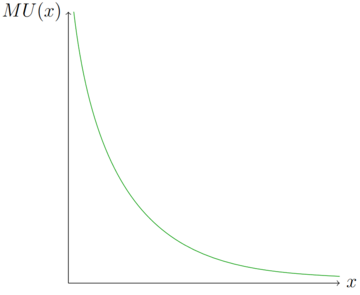
In den Abbildungen oben wird der Bezug zwischen der Grenznutzenfunktion (MU(x)) und der Nutzenfunktion (U(x)) deutlich. Die marginale Steigung in einem Punkt entspricht dem Grenznutzen in diesem Punkt. Grundsätzlich ist es auch möglich einen steigenden Grenznutzen darzustellen. In diesem Fall wäre die Nutzenfunktion konvex und nicht konkav, wie oben dargestellt.
Grenzkosten
Grenzprodukt
Das Grenzprodukt betrachtet, wie sich der Output verhält, wenn der Input marginal erhöht wird.