Vergleich Gewinnmaximum bei unterschiedlichen Marktformen: Unterschied zwischen den Versionen
Lobin (Diskussion | Beiträge) |
|||
| Zeile 7: | Zeile 7: | ||
Gewinnfunktionen setzen sich aus dem Umsatz und den Kosten zusammen. <br> | Gewinnfunktionen setzen sich aus dem Umsatz und den Kosten zusammen. <br> | ||
<math> \Pi=Umsatz-Kosten </math> <br> | <math> \Pi=Umsatz-Kosten </math> <br> | ||
| − | Bei einer konkaven Gewinnfunktion existiert ein Gewinnmaximum. Eine marginale zusätzliche Einheit würde den Gewinn nicht mehr erhöhen (≙ Die erste Ableitung der Gewinnfunktion muss gleich null sein) <br> | + | Bei einer konkaven Gewinnfunktion existiert ein Gewinnmaximum. Eine marginale zusätzliche Einheit würde den Gewinn nicht mehr erhöhen (≙ Die erste Ableitung der Gewinnfunktion muss gleich null sein). <br> |
<math> \frac{\part \Pi}{\part Q}=\frac{\part Umsatz}{\part Q}-\frac{\part Kosten}{\part Q}=Grenzumsatz-Grenzkosten=0 </math> <br> | <math> \frac{\part \Pi}{\part Q}=\frac{\part Umsatz}{\part Q}-\frac{\part Kosten}{\part Q}=Grenzumsatz-Grenzkosten=0 </math> <br> | ||
Umgestellt bedeutet dies, dass der Grenzumsatz gleich den Grenzkosten sein muss. Da die Gewinnfunktion unabhängig von der [[Marktformen|Marktform]] aus dem Umsatz und den Kosten besteht, gilt die Grenzumsatz gleich Grenzkosten Relation ebenfalls immer. Der Unterschied besteht im Grenzumsatz und wie sich dieser zusammensetzt. | Umgestellt bedeutet dies, dass der Grenzumsatz gleich den Grenzkosten sein muss. Da die Gewinnfunktion unabhängig von der [[Marktformen|Marktform]] aus dem Umsatz und den Kosten besteht, gilt die Grenzumsatz gleich Grenzkosten Relation ebenfalls immer. Der Unterschied besteht im Grenzumsatz und wie sich dieser zusammensetzt. | ||
Version vom 23. August 2023, 16:29 Uhr
Das Ziel von Unternehmen (bei Annahme des homo economicus) ist unabhängig von der Marktform, in der sie agieren, ihren Gewinn zu maximieren.
Die Gewinnfunktion
Gewinnfunktionen setzen sich aus dem Umsatz und den Kosten zusammen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Pi=Umsatz-Kosten }
Bei einer konkaven Gewinnfunktion existiert ein Gewinnmaximum. Eine marginale zusätzliche Einheit würde den Gewinn nicht mehr erhöhen (≙ Die erste Ableitung der Gewinnfunktion muss gleich null sein).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part \Pi}{\part Q}=\frac{\part Umsatz}{\part Q}-\frac{\part Kosten}{\part Q}=Grenzumsatz-Grenzkosten=0 }
Umgestellt bedeutet dies, dass der Grenzumsatz gleich den Grenzkosten sein muss. Da die Gewinnfunktion unabhängig von der Marktform aus dem Umsatz und den Kosten besteht, gilt die Grenzumsatz gleich Grenzkosten Relation ebenfalls immer. Der Unterschied besteht im Grenzumsatz und wie sich dieser zusammensetzt.
Gewinnmaximierung im perfekten Wettbewerb
Im perfekten Wettbewerb sind alle Akteure, so auch die Produzenten, Preisnehmer. Sie können den Marktpreis nicht beeinflussen und sehen sich daher einer horizontalen Nachfragefunktion gegenüber.
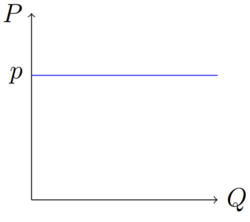
Der Marktpreis p ist dementsprechend der Preis, den die Produzenten für jede abgesetzte Einheit jeweils erhalten. Der Umsatz ergibt sich aus der abgesetzten Menge multipliziert mit dem Preis (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Umsatz=p*Q }
). Werden beispielsweise 5 Tafeln Schokolade von einer Schokoladenfabrik auf einem Markt mit dem Marktpreis 2€ abgesetzt, beträgt der Umsatz 10€ (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Umsatz=2*5}
). Der Grenzumsatz ergibt sich aus der Ableitung des Umsatzes nach Q. In diesem Falle ist der Grenzumsatz gleich dem Marktpreis p.
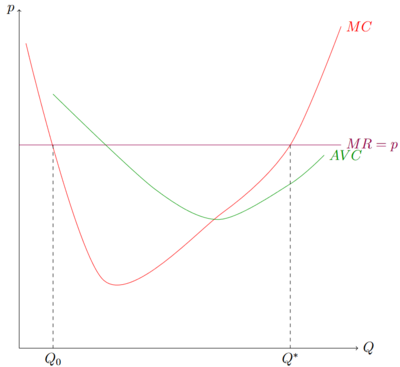
In der obigen Grafik sind die Grenzkosten (MC) zweimal gleich dem Grenzumsatz (MR) (zwei Schnittpunkte). Die Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q_{0}}
maximiert jedoch den Gewinn nicht, da bei einer Erhöhung der Produktionsmenge die Grenzkosten kleiner als der Grenzumsatz sind. Bei jeder weiteren marginalen Einheit sind die Kosten von dieser in der Produktion kleiner, als der Marktpreis. Bei der Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q^*}
sind die Kosten der marginalen Einheit größer, als diese Umsatz bringt. Eine Erhöhung der Outputmenge ist daher nicht sinnvoll.
Gewinnmaximierung im Monopol
Das Monopol stellt in Bezug auf die Marktmacht von Unternehmen das Gegenteil zum perfekten Wettbewerb dar. Ein Monopolist ist das als einzige auf dem Markt agierende Unternehmen. Dementsprechend besitzt es einen erheblichen Einfluss auf die Preisbildung. Angenommen es existiert nur ein Unternehmen auf dem Smartphone Markt und Smartphones sind durch kein anderes Gut substituierbar. Produziert das Unternehmen nur eine geringe Anzahl an Smartphones, kann das Unternehmen einen hohen Preis verlangen. Steigert das Unternehmen die Produktionsmenge, ist die Knappheit nicht mehr so groß und der Preis für Smartphones sinkt in der Folge. Welche Menge zu welchem Preis nachgefragt wird stellt sich in der Nachfragefunktion dar. Anders als bei der Gewinnmaximierung im perfekten Wettbewerb verändert sich dementsprechend der Preis mit der Produktionsmenge des Produzenten, der Preis ist eine von der Menge abhängigen Funktion (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(Q_N)}
).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Umsatz=P(Q_N) Q}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part Umsatz}{\part Q}=p'(Q) Q+p(Q)}
Bei Annahme einer linearen Nachfragefunktion ist die Grenzumsatzfunktion (MR(Q)) doppelt so steil wie die Nachfragefunktion. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P=a-bQ}
die Angebotsfunktion, dann ist b die Steigung und es ergibt sich folgendes:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Umsatz=p*Q=(a-bQ) Q=aQ-bQ^2}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part Umsatz}{\part Q}=a-2bQ}
Im Gewinnoptimum gilt Grenzumsatz=Grenzkosten:
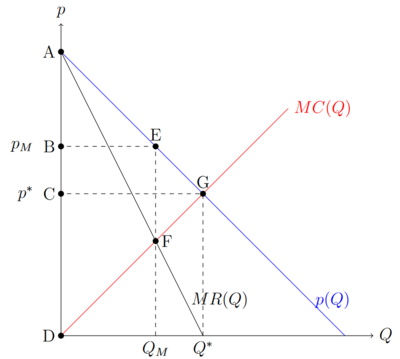
Der Monopolpreis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p^M }
ist größer als der Preis im perfekten Wettbewerb Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p^* }
und die abgesetzte Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q_M}
ist geringer. Dies schmälert die Gesamtwohlfahrt und stellt eine Ineffizienz dar.
Ein Monopolist produziert niemals im unelastischen Bereich der Nachfragefunktion. Dies kann grafisch geziegt werden, denn selbst bei Grenzkosten gleich null liegt der Monopolpreis bei einer Preiselastizität der Nachfrage, die betragsmäßig gleich eins ist. Es kann jedoch auch mathematisch bewiesen werden. Nach der ersten Ableitungen des Monopolgewinns ergibt sich
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P=C'\biggl(\frac{1}{1-\frac{1}{\epsilon}}\biggr) }
bei einer positiv definierten Elastizität und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P=C'\biggl(\frac{1}{1+\frac{1}{\epsilon}}\biggr) }
bei einer negativ definierten Elastizität. In beiden Fällen ist der Preis größer, je unelastischer die Nachfrage ist (vorrausgesetzt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C'>0 }
). Im unelastischen Bereich ist die Elastizität betragsmäßig kleiner als eins und es käme ein Preis geringer als die Grenzkosten heraus.
Gewinnmaximierung im Oligopol
Oligopolistische Wettbewerbe sind durch angebotsseitige Marktmacht geprägt. Diese entsteht durch wenige Anbieter und viele Nachfrager. In der Gewinnmaximierung muss auf verschiedene Aspekte eingegangen werden wie zum Beispiel sind die Güter differenziert oder nicht und befinden sich die Unternehmen in einem Preis- oder Mengenwettbewerb. Grundsätzlich gilt es auch hier die Gewinnfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi_i=p_1 q_1-c(q_i) } zu maximieren. Auf die genauen Spezifikationen wird hier nochmal tief gehender eingegangen.
MC Fragen