Maximieren: Unterschied zwischen den Versionen
Lobin (Diskussion | Beiträge) |
Lobin (Diskussion | Beiträge) |
||
| Zeile 19: | Zeile 19: | ||
==Bedingung zweiter Ordnung== | ==Bedingung zweiter Ordnung== | ||
Die Bedingung zweiter Ordnung (oder auch hinreichende Bedingung) lautet ergänzend zu der Bedingung erster Ordnung <math> f''(x)<0 </math> für einen Hochpunkt und <math> f''(x)>0 </math> für einen Tiefpunkt. <br> | Die Bedingung zweiter Ordnung (oder auch hinreichende Bedingung) lautet ergänzend zu der Bedingung erster Ordnung <math> f''(x)<0 </math> für einen Hochpunkt und <math> f''(x)>0 </math> für einen Tiefpunkt. <br> | ||
| − | Die Bedingung zweiter Ordnung untersucht die Steigung der ersten Ableitung. Die Formeln lassen sich bereits mit den Abbildungen oben erläutern. Bei einem Hochpunkt ist die Steigung linksseitig vom Extrempunkt positiv und nähert sich null an. Nach dem Extrempunkt ist die Steigung negativ | + | Die Bedingung zweiter Ordnung untersucht die Steigung der ersten Ableitung. Die Formeln lassen sich bereits mit den Abbildungen oben erläutern. Bei einem Hochpunkt ist die Steigung linksseitig vom Extrempunkt positiv und nähert sich null an. Nach dem Extrempunkt ist die Steigung negativ. Bei den Abbildungen unten sind die Formeln noch intuitiver erklärt. <br> |
[[Datei:Hochpunkt2.png|300px|rahmenlos]] | [[Datei:Hochpunkt2.png|300px|rahmenlos]] | ||
[[Datei:Tiefpunkt2.png|300px|rahmenlos]] <br clear=all> | [[Datei:Tiefpunkt2.png|300px|rahmenlos]] <br clear=all> | ||
Version vom 12. September 2023, 13:03 Uhr
Das Maximieren von Funktionen wird genutzt, um lokale und globale Extremstellen (Maxima) von Funktionen zu finden.
Maximieren
Ein lokaler Hochpunkt ist ein Punkt auf einer Funktion, dessen x-Wert in seiner lokalen Umgebung, der höchste y-Wert zugeordnet wird. Wird in der Funktionsgleichung ein etwas kleinerer oder etwas größerer x-Wert eingesetzt, kommt immer ein kleinerer y-Wert raus als im lokalen Optimum. Der Hochpunkt ist auch ein globaler Hochpunkt, wenn dies nicht nur für die marginale Umgebung, sondern für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \in \mathbb{R} }
gilt. Vor einem Hochpunkt steigt dementsprechend die Funktion und nach dem Hochpunkt sinkt sie.
Bei einem lokalen Tiefpunkt ist der y-Wert lokal der niedrigste und nicht der größte.
In der Analyse auf Extrempunkte ist die Steigung ein entscheidender Faktor. Hierfür werden zwei Bedingungen aufgestellt.
Bedingung erster Ordnung
Die Bedingung erster Ordnung (oder auch Notwendige Bedingung) lautet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f'(x)\overset{!}{=}0 }
Wenn bei einem Extrempunkt die Funktion erst steigt und dann fällt oder andersherum, muss es im Extremum einen Punkt geben, in dem die Funktion weder steigt noch fällt und eine Steigung von 0 hat. Die erste Ableitung beschreibt die Steigung der Funktion und wird daher auch Steigungsfunktion genannt. Sie bestimmt die Steigung der Funktion in jedem x-Wert. Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)\overset{!}{=}0 }
ist der Punkt gesucht, in dem die Steigung gleich null ist.
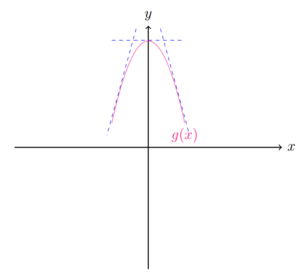
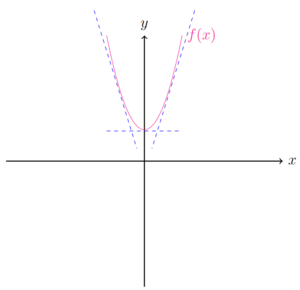
Im Extrempunkt, egal ob Hochpunkt oder Tiefpunkt, ist die Steigung der Funktion null. Eine Tangente, die die Steigung in dem Punkt beschreibt, ist eine horizontale Gerade. Ein Steigungsdreieck an der Tangente würde rechnerisch eine Steigung von null ergeben.
Die Bedingung erster Ordnung untersucht, ob ein Extrempunkt vorliegt.
Bedingung zweiter Ordnung
Die Bedingung zweiter Ordnung (oder auch hinreichende Bedingung) lautet ergänzend zu der Bedingung erster Ordnung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f''(x)<0 }
für einen Hochpunkt und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f''(x)>0 }
für einen Tiefpunkt.
Die Bedingung zweiter Ordnung untersucht die Steigung der ersten Ableitung. Die Formeln lassen sich bereits mit den Abbildungen oben erläutern. Bei einem Hochpunkt ist die Steigung linksseitig vom Extrempunkt positiv und nähert sich null an. Nach dem Extrempunkt ist die Steigung negativ. Bei den Abbildungen unten sind die Formeln noch intuitiver erklärt.
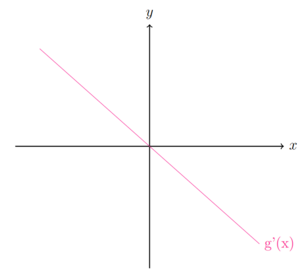
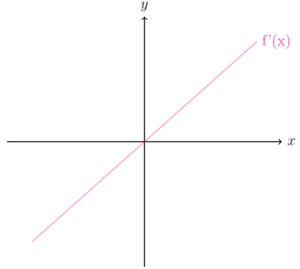
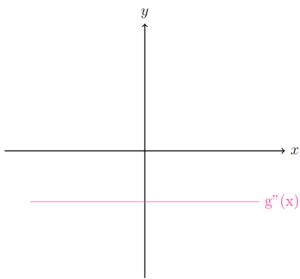
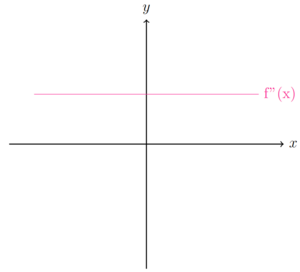
Ist die Steigung der ersten Ableitung (g'(x)) negativ, wird die Steigung der Funktion (g(x)) mit der Zeit immer kleiner. Die Steigung der Funktion ist erst positiv und wird immer kleiner, bis sie bei null liegt. In diesem Punkt wird die Steigung noch immer kleiner und daher negativ.
Mathematisch formal ist es notwendig die Extremstellen auch auf die zweite Bedingung zu untersuchen. Zum einen, um herauszufinden welcher der beiden Fälle vorliegt und zum anderen, um andere mathematische Eigenschaften wie einen Sattelpunkt auszuschließen. In der OMIK sind die Funktionen jedoch recht simpel, sodass häufig schon an der Funktion abgelesen werden kann, ob es sich um ein Hochpunkt oder Tiefpunkt handelt.
Gewinnfunktion
In der Mikroökonomie gilt es häufig eine Unternehmensentscheidung zu treffen, wie viel ein Unternehmen gewinnmaximal anbieten soll. Die Frage ist dementsprechend: Bei welcher Menge q ist der Gewinn maximal. Hierfür ist die Gewinnfunktion notwendig.
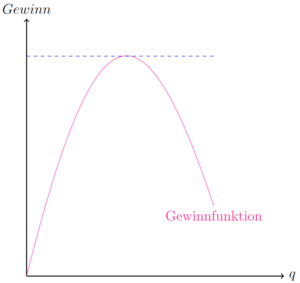
Die Gewinnfunktion ist in den meisten Fällen eine quadratische Funktion, die nach unten geöffnet ist. In der Frage, welche Menge gewinnmaximal ist, muss untersucht werden, zu welchem q-Wert der größte Gewinn zugeordnet werden kann. Um den Punkt rechnerisch zu bestimmen kann die erste Ableitung der Gewinnfunktion gebildet und berechnet werden, bei welchem q-Wert die erste Ableitung gleich null ist.
MC Fragen