Mathematische Eigenschaften von Funktionen: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 21: | Zeile 21: | ||
==Steigung== | ==Steigung== | ||
| − | Die Steigung einer Funktion kann punktuell ([[margiale Sichtweise|marginal]]) oder auch zwischen zwei Punkten ermittelt werden. | + | Die Steigung einer Funktion kann punktuell ([[margiale Sichtweise|marginal]]) oder auch zwischen zwei Punkten ermittelt werden. Die Steigung ermittelt die Veränderung der abhängigen Varaible relativ zur Veränderung der unabhängigen Variable. Angenommen die unabhängige Variable ist x und die abhängige Variable ist y, dann lässt sich die Steigung mittels <br> |
| + | <math> Steigung=\frac{\Delta y}{\Delta x}=\frac{y_1-y_2}{x_1-x_2}=\frac{y_2-y_1}{x_2-x_1} </math> <br> | ||
| + | berechnen. Ist die Steigung in einem Punkt gefragt, muss das <math> \Delta x </math> gegen null streben. Dieses Vorgehen ist im Differenzenquotienten beschrieben und hat die erste Ableitung zur Folge. Die erste Ableitung gibt das Steigungsdreieck in einem marginalen Punkt an. In dem unten dargestellten Beispiel wird die Differenz zwischen den beiden Punkten <math> x=4 </math> und <math> x=8 </math> verringert, in dem der Punkt, der ursprünglich in <math> x=4 </math> lag, immer weiter Richtung <math> x=8 </math> verschoben wird, bis er auf diesem Punkt liegt (<math> \Delta x \to 0 </math>). <br> | ||
| + | [[Datei:Funktion2.png|400px|rahmenlos]] | ||
| + | [[Datei:Funktion3.png|400px|rahmenlos]] | ||
| + | <br> | ||
| + | <br clear=all> | ||
| + | Die Steigung in der linken Abbildung lässt sich durch <math> \frac{4-1}{8-4}=0,75 </math> berechnen. Für die Steigung der recten Abbildung benötigt es die erste Ableitung. Die erste Ableitung einer Funktion wird auch Steigungsfunktion genannt, da der y-Wert der ersten Ableitung immer die Steigung in einem Punkt der ursprüngliche Funktion angibt. Wenn nun die Steigung in dem Punkt <math> x=8 </math> gefragt ist, muss <math> x=8 </math> in die erste Ableitung eingesetzt werden. Die Funktion lautet <math> f(x)=\frac{1}{16}x^2 </math> und die erste Ableitung daher <math> f'(x)=\frac{1}{8}x </math>. Mit <math> f(8) </math> ergibt sich die Steigung von 1. | ||
==Konvex und Konkav== | ==Konvex und Konkav== | ||
Version vom 12. September 2023, 14:33 Uhr
Definition
Eine Funktion ordnet einer unabhängigen Variable eines Definitionsbereichs (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D }
) genau einen Wert (abhängige Variable) der Zielmenge (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z }
) zu.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D \to Z }
, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x\to y }
Funktionen
Funktionen können univariat oder auch multivriat sein. Der Unterschied besteht darin, wie viele unabhängige Variablen Teil der Funktionsgleichung sind.
Univariate Funktionen
Am bekanntesten sind sicherlich univariate Funktionen mit nur einer unabhängigen Variable. Eine unabhängige Variable wird so genannt, da sie von keineren weiteren Variablen abhängig ist.
Beispiel: In der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y(x)=15-2x^2 }
ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x }
von nichts abhängig. Für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x}
können alle Werte eingesetzt werden, sollte kein anderer Definitionsbereich festgelegt sein. y ist hingegen abhängig von x. Jenachdem welcher x Wert eingesetzt wird, ändert sich der Wert von y.
Eine Funktionsgleichung kann als eine Art Anleitung gelesen werden. Lautet die Funktion beispielsweise Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y(x)=x^2+10}
, wäre die Anleitung "Um den zum x zugehörigen y Wert zu erhalten, nehme den entsprechenden x-Wert, quadriere ihn und addiere 10 dazu". Ist x beispielsweise 2, ist y 14. Wird dies mit mehreren x Werten berechnet und die entsprechenden Werte in ein x-y-Diagramm eingezeichnet, entsteht ein Graph, der die Funktionsgleichung abbildet.
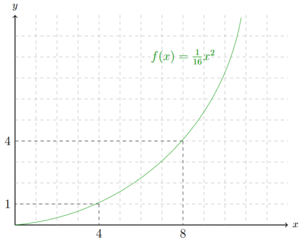
In dem Beispiel oben ist dies mit der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=\frac{1}{16}x^2 }
geschehen. Jedem x-Wert kann ein y-Wert zugeordnet werden.
Multivariate Funktionen
Multivariate Funktionen haben viele unabhängige Variablen. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x_1,x_2,x_3,...,x_n) }
ist eine Multivariate Funktion mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n }
unabhängigen Variablen. Die Vorgehensweise ist identisch zu univariaten Funktionen. Zur grafischen Darstellung soll eine Bivriate Funktion ausreichen. In diesem Fall lautet die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(C,F)=F^{\frac{2}{3}}C^{\frac{1}{3}} }
. Für einen bestimmten Wert von C und von F kommt ein Wert für U aus. Ist C beispielsweise 1 und F 0,5, beträgt der Wert von U gerundet 0,63. Wird dies für alle Werte für C und F gemacht, ergibt sich eine grafische Abbildung der Funktion.
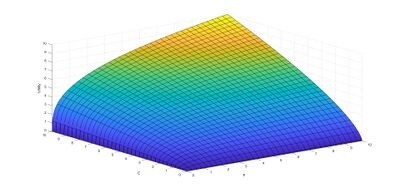
Im Kontext der Veranstaltung Mikroökonomie sind sowohl univariate, als auch multivariate Funktionen relevant.
Steigung
Die Steigung einer Funktion kann punktuell (marginal) oder auch zwischen zwei Punkten ermittelt werden. Die Steigung ermittelt die Veränderung der abhängigen Varaible relativ zur Veränderung der unabhängigen Variable. Angenommen die unabhängige Variable ist x und die abhängige Variable ist y, dann lässt sich die Steigung mittels
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Steigung=\frac{\Delta y}{\Delta x}=\frac{y_1-y_2}{x_1-x_2}=\frac{y_2-y_1}{x_2-x_1} }
berechnen. Ist die Steigung in einem Punkt gefragt, muss das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta x }
gegen null streben. Dieses Vorgehen ist im Differenzenquotienten beschrieben und hat die erste Ableitung zur Folge. Die erste Ableitung gibt das Steigungsdreieck in einem marginalen Punkt an. In dem unten dargestellten Beispiel wird die Differenz zwischen den beiden Punkten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=4 }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=8 }
verringert, in dem der Punkt, der ursprünglich in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=4 }
lag, immer weiter Richtung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=8 }
verschoben wird, bis er auf diesem Punkt liegt (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta x \to 0 }
).
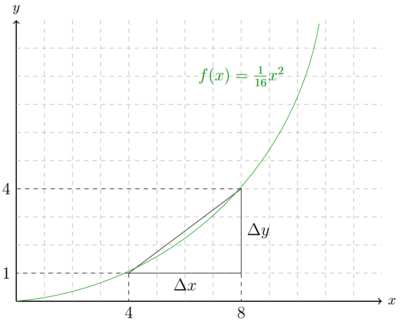
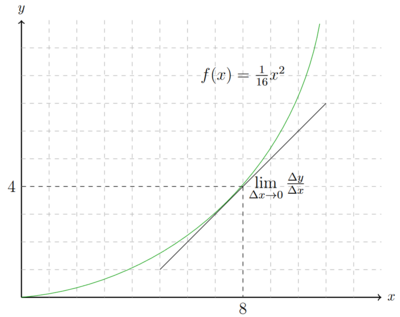
Die Steigung in der linken Abbildung lässt sich durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{4-1}{8-4}=0,75 }
berechnen. Für die Steigung der recten Abbildung benötigt es die erste Ableitung. Die erste Ableitung einer Funktion wird auch Steigungsfunktion genannt, da der y-Wert der ersten Ableitung immer die Steigung in einem Punkt der ursprüngliche Funktion angibt. Wenn nun die Steigung in dem Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=8 }
gefragt ist, muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=8 }
in die erste Ableitung eingesetzt werden. Die Funktion lautet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=\frac{1}{16}x^2 }
und die erste Ableitung daher Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f'(x)=\frac{1}{8}x }
. Mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(8) }
ergibt sich die Steigung von 1.