Marginale Sichtweise

Definition

Die Marginalanalyse untersucht in der Volkswirtschaftslehre, welchen Effekt eine geringfügige Änderung einer Variablen auf eine oder mehrere andere Variablen hat.

Veränderung zwischen zwei Punkten

In der Mikroökonomie wird häufig untersucht, wie sich beispielsweise ein Nutzen verändert, wenn sich die Anzahl der konsumierten Güter verändern. Genauso können Kosten, der Output oder andere Dinge, die durch Funktionen berechnet werden, Gegenstand von Untersuchungen sein. Im weiteren Verlauf soll sich auf eine Nutzenfunktion mit einem Konsumgut konzentriert werden. Die Implikationen gelten jedoch auch für Nutzenfunktionen mit mehreren Konsumgütern oder die anderen aufgezählten Fälle.
In der Grafik unten wird berechnet, wie sich das Nutzenniveau verändert, wenn von einem Konsumgut x deutlich mehr konsumiert wird. Hierfür wird das Nutzenniveau von einem alten Konsumniveau mit dem Nutzenniveau eines erhöhten Konsumniveaus verglichen. Liegt das derzeitige Konsumniveau beispielsweise bei x=10 und es soll untersucht werden, um wie viel Einheiten sich der Nutzen verändert hat, wenn 2 weitere Einheiten konsumiert werden, muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(10+2)-U(10) } gerechnet werden. Diese Vorgehensweise gibt einen numerischen Wert.


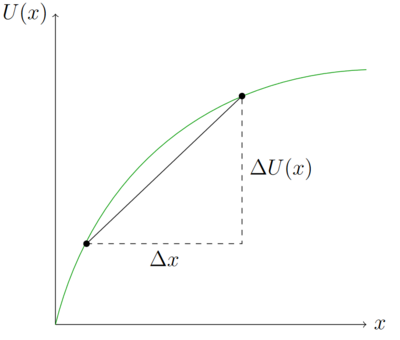
Die Untersuchung auf Veränderungen auf zwei Punkten auf einer Funktion kann zu falschen Aussagen über Konsumentscheidungen führen. In der Abbildung unten besitzt die Nutzenfunktion einen Hochpunkt und der erste Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } liegt beispielweise links vom Hochpunkt. Der andere Punkt (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } ) liegt rechts von diesem auf einem niedrigeren Nutzenniveau als Punkt $x_{1}$. Soll nun ein Berater eine Aussage über das Konsumverhalten treffen und kennt die Nutzenfunktion nicht, könnte er zu einer falschen Empfehlung kommen das Nutzenniveau nicht zu verändern oder sogar zu reduzieren. Tatsächlich wäre es optimal das Konsumniveau bis zum Hochpunkt auszuweiten. Um korrekte Aussagen über die Konsumentscheidungen treffen zu können, benötigt es eine Untersuchung der Veränderung in einem Punkt.

Veränderung in einem Punk

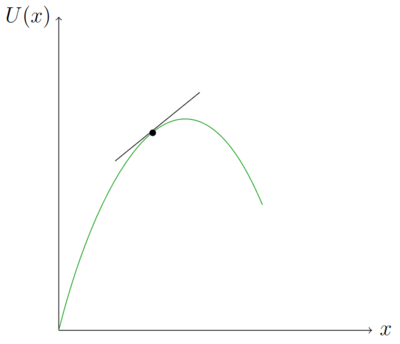
Aussagen über Konsumentscheidungen, also ob mehr oder weniger von einem Gut konsumiert werden sollte, lassen sich nicht immer auf Basis von Veränderungen zwischen zwei Punkten treffen. Viel entscheidender ist die Untersuchung, wie sich das Nutzenniveau verhält, wenn sich das Konsumniveau sehr gering ändert. Steigt beispielweise der Nutzen, wenn ein Konsument zusätzlich zu seinen 10 Äpfeln auch noch etwas mehr isst. Steigt das Nutzenniveau durch den zusätzlichen Apfelkonsum, sollte der Konsument seinen Konsum steigern, sinkt es allerdings, sollte er es vermeiden. In der Abbildung unten ist zu erkennen, dass die Steigung in dem Punkt $x$ positiv ist. Der Nutzen steigt also, wenn der Konsument etwas mehr Äpfel ist als die Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } . Geichzeitig wird jedoch auchdeutlich, dass der Konsum eines zusätzlichen ganzen Apfels (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x+1 } ) das Nutzenniveau erneut schmälert und nicht steigert. Anstatt zu untersuchen, wie es sich mit dreiviertel eines Apfels, einem halben Apfel usw. verhält, wird untersucht, wie sich das Nutzenniveau bei einer kleinst möglichen Veränderung der konsumierten Menge verändert. Entscheiden ist also die Veränderung möglichst gering zu halten. Die Untersuchung in einem Punkt ist dementsprechend so zu verstehen, dass sich die Menge insofern verändert, als dass diese Veränderung mit Zahlen nicht zu beziffern, sondern so klein ist, als würde die Veränderung gar nicht stattfinden. Es wird dabei auch von einer marginalen Veränderung gesprochen.


Die Abbildung oben veranschaulicht, dass mit einer margialen Veränderung, die Veränderung in einem Punkt gemeint ist. Die Tangente in dem Punkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x } mit der Nutzenfunktion weißt eine positive Steigung aus. Würde sich das Konsumniveau um eine Einheit erhöhen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x+1 } , zeigt die Tangente, dass das Konsumniveau größer als vorher ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U'(x+1)> U(x) } . Tatsächlich liegt das Nutzenniveau bei $U(x+1)$, was geringer als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U'(x+1) } ist.

Marginale Veränderung

In der Volskwirtschaftslehre und insbesonder der Mikroökonomie ist häufig von einem marginalen Effekt die Rede. Dieser marginale Effekt betrachtet, wie sich was verändert, wenn eine Variable sehr gering, also marginal, erhöht wird. In dem oben genannten Beispiel wird untersucht, wie groß der Effekt ist, wenn eine zusätzliche marginale Einheit konsumiert wird. Wie groß diese marginale Einheit ist, kann nicht genau bemessen werden. Es ist schlichtweg die Veränderung in einem Punkt.
Der marginale Effekt lässt sich durch die Ableitung nach der zu betrachtenden Variable berechnen. Die erste Ableitung einer Funktion gibt die Steigung in dem Punkt des x-Wertes an. Genauso gibt die Ableitung, beispielsweise der Nutzenfunktion an, wie sich der Nutzen marginal in diesem Punkt verändert. Ist die erste Ableitung in de zu betrachtenden Punkt positiv (wie in dem Beispiel unten), steigt das Nutzenniveau bei marginaler Erhöhung des Konsumniveaus. Eine Tangente in diesem Punkt hat eine positive Steigung. Ist die erste Ableitug negativ in dem Punkt, bzw. hat die Tangente in diesem Punkt eine negative Steigung, sinkt das Nutzenniveau bei einer marginalen Erhöhung des Konsumniveaus. Die marginale Betrachtung wird auch häufig Grenzbetrachtung genannt, weshalb der Begriff Grenznutzen die Veränderung des Nutzen bei marginaler Veränderung des Konsumniveaus beschreibt.
Diese Marginalbetrachtung/Grenzbetrachtung lässt, anders als die Betrachtungsweisen oben (Veränderung zwischen zwei Punkten und eine Veränderung um eine nominale Einheit), korrekte Aussagen über Konsumentscheidungen zu. Ein positiver Grenznutzen bedeutet der Nutzen steigt bei marginaler Erhöhung des Konsumniveaus, dementsprechend sollte marginal mehr konsumiert werden.

Grenznutzen

Produktivität, Nutzen, Output und viele andere Sachen können auf marginale Effekte untersucht werden. Ganz explizit als Beispiel soll erneut der Nutzen als Beispiel dienen.
Wie in dem Abschnitt oben bereits erläutert wurde, gilt es die Veränderung des Nutzennvieaus in einem Punkt zu bestimmen. Ob es ratsam ist das Konsumniveau marginal zu erhöhen lässt sich schnell durch die Steigung in diesem Punkt ermitteln. Ist die Steigung positiv (eine Tangente in dem Punkt mit der Nutzenfunktion hat eine positive Steigung), sollte der Kosum marginal erhöht werden. Für die Untersuchung wie es sich entlang der gesamten Nutzenfunktion verhält, dient die erste Ableitung der Nutzenfunktion. Diese gibt für jedes beliebige Konsumniveau an, ob das Nutzenniveau in dem Punkt marginal steigt, sinkt oder konstant bleibt. Wie sich der Nutzen bei einer marginalen Veräderung verhält wird im Grenznutzen beschrieben. Der Der Grenznutzen (GU oder MU) untersucht, wie sich der Nutzen verhält, wenn das Konsumniveau marginal erhöht wird. In der Theorie wird von einem abnehmenden Grenznutzen ausgegangen.
Beispiel: Nach dem erfolgreichen Bachelor beschließt Tom bei einer Bank fest einzusteigen. Er besitzt keinen Anzug und geht deshalb einkaufen. Er kauft einen ersten Anzug, ohne den er fast gar nicht arbeiten könnte. Der Nutzen, den der erste Anzug stiftet ist sehr groß. Tom kauft einen zweiten Anzug, falls der erste dreckig wird. Auch der zweite Anzug stiftet einen großen Anzug, jedoch einen nicht so großen, wie der erste. Je mehr Anzüge Tom kauft, desto größer wird sein Nutzen. Jeder einzelne Anzug stiftet jedoch einen imemr kleiner werdenden zusätzlichen Nutzen. Der Nutzen einer marginalen Einheit mehr ist positiv, wird aber immer kleiner. In dem Beispiel wird ein Anzug als eine marginale Einheit beschrieben. Dies ist, wie oben erklärt, nicht ganz richtig, soll aber zur Veranschaulichung des Grenzbegriffs ausreichen.
Der Grenznutzen lässt sich durch die Ableitung der Nutzenfunktion berechnen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle MU=\frac{\part U(x)}{\part x} }

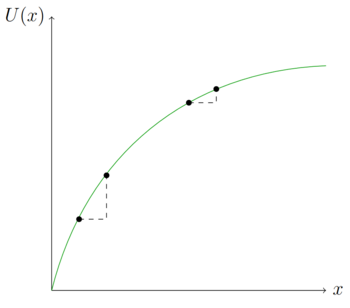
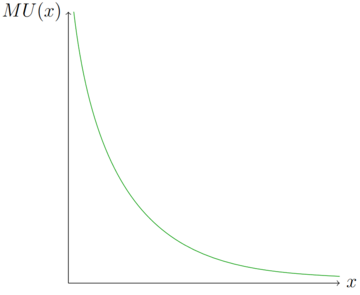
In den Abbildungen oben wird der Bezug zwischen der Grenznutzenfunktion (MU(x)) und der Nutzenfunktion (U(x)) deutlich. Die marginale Steigung in einem Punkt entspricht dem Grenznutzen in diesem Punkt. Grundsätzlich ist es auch möglich einen steigenden Grenznutzen darzustellen. In diesem Fall wäre die Nutzenfunktion konvex und nicht konkav, wie oben dargestellt.