Axiome der Nutzentheorie: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 51: | Zeile 51: | ||
- Lokale Nicht Sättigung | - Lokale Nicht Sättigung | ||
+ Monotonie | + Monotonie | ||
| + | </quiz> | ||
| + | |||
| + | [[Datei:AxiomMC2.png|250px|rahmenlos]] | ||
| + | <quiz display=simple shuffleanswers=true> | ||
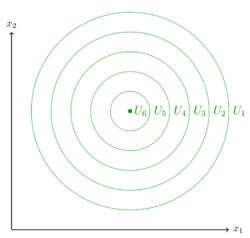
| + | {Welche Annahme über Präferenzen ist in der Abbildung oben verletzt, wenn <math> U_1<U_2<U_3<... </math> gilt? | ||
| + | |type="()"} | ||
| + | - Transitivität | ||
| + | - Vollständigkeit | ||
| + | + Lokale Nicht Sättigung | ||
| + | - Rationalität | ||
</quiz> | </quiz> | ||
Version vom 5. Oktober 2023, 13:44 Uhr
Konsumenten besitzen Präferenzen, die sie beispielsweise im Konsumverhalten aufweisen. Damit viele Modelle konsistent und plausibel sind, müssen Annahmen über Präferenzen getroffen werden, die auch Axiome gennant werden. Im Weiteren muss zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle > } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \succ } unterschieden werden. Ersteres zeigt an, dass die linke Seite größer ist als die rechte. Zweiteres gibt an, dass die linke Seite gegenüber der rechten präferiert wird.
Rationalität
Präferenzen sind rational, wenn sie vollständig und transitiv sind.
Vollständigkeit
Vollständigkeit: für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x,y \in X}
, muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \succeq y }
oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y \succeq x }
(oder beides) gelten.
Die formale Schreibweise oben beschreibt die Annahme, dass Konsumenten von allen möglichen Auswahlmöglichkeiten (X) diese untereinander bewerten können. Das heißt ein Konsument präferiert besipielsweise ein Konsumgüterbündel x einem Bündel y oders andersherum. Alternativ kann ein Konsument auch indifferent zwischen den beiden Konsumgüterbündeln sein. In diesem Fall spielt es für den Konsumenten keine Rolle ob er sich für x oder für y entscheidet. Vollständige Präferenzen schließen explizit den Fall aus, in dem sich ein Konsument nicht entscheiden kann.
Beispiel für vollständige Präferenzen: In einem Kino gibt es zusätzlich zu einer Kinokarte auch ein Snack-Menü gratis zur Auswahl. Arun besucht dieses Kino und hat die Wahl zwischen einer kleinen Portion Popcorn mit einem halben Liter Cola (Konsumbündel x) und einer großen Portion Popcorn ohne Getränk (Konsumbündel y). Besitzt Arun vollständige Präferenzen, präferiert er den Fall x gegenüber dem Bündel y (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \succeq y}
), er präferiert Bündel y gegenüber dem Bündel x (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y \succeq x }
) oder er ist indifferent (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \backsim y}
).
Transitivität
Transitivität: Für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x,y,z \in X }
muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \succeq z }
gelten, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \succeq y }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y \succeq z }
gilt.
Transitivität sichert, dass die Konsumentenpräferenzen konsistent und somit rational sind. Ähnlichkeit besteht zu Größenverhältnissen: wenn Lisa größer ist als Anna und diese größerals Sarah, dann ist Lisa auch größer als Sarah. Nicht in allen Situationen halten vergleichende Beziehungen der Transitivitätsannahme stand. So bedeutet der Umstand, dass Schalke04 gegen den Borussia Dortmund gewonnen hat und Schalke gegen Bayern München verloren hat, noch lange nicht, dass Dortmund gegen die Bayern verliert.
Die mathematische Schreibweise oben beschreiben, dass die Güter als besser oder gleich wahrgenommen werden. Die Transitivitätsannahme hält auch für strikt präferierte Konsumgüterbündel. Gleichzeitig gilt die Annahme auch, wenn ein Konsument indifferent zwischen den verschiedenen Konsumgüterbündel ist:
Für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x,y,z \in X }
muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \succ z }
gelten, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \succ y }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y \succ z }
gilt.
Für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x,y,z \in X }
muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \backsim z }
gelten, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \backsim y }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y \backsim z }
gilt.
Lokale Nicht Sättigung
Lokale Nicht Sättigung: für alle und jedem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon \in X }
existiert ein Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y \in X }
für das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle ||y-x||\leq \epsilon }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y \succ x }
gilt.
Die mathematische Schreibweise der lokalen Sättigung beschreibt das Phänomen, dass bei vorliegen der lokalen Nichtsättigung ein y in der Nähe von x existiert, dass gegenüber y präferiert wird. Das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \epsilon }
ist hierbei der Abstand zwischen x und y, der betragsmäßig sehr klein sein soll (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle ||y-x||\leq \epsilon }
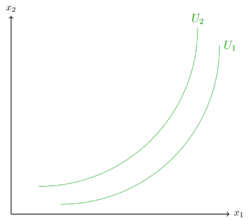
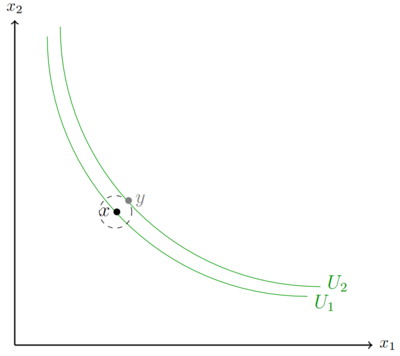
). Dies lässt sich als eine Art Ball um den Punkt x verstehen. Kann durch minimale Anpassungen des Konsumpunkts das Nutzenniveau erhöht werden, wird die Annahme der lokalen Nicht Sättigung nicht verletzt. Grafisch muss eine Indifferenzkurve nahe der alten Indifferenzkurve, auf der sich der Punkt x befindet, ein höheres Nutzenniveau bedeuten, damit die Annahme nicht verletzt ist. Ein neuer Punkt y kann irgendwo auf dem gestrichelten Ball liegen. Egal ob die neue Indifferenzkurve überhalb, unterhalb, rechts oder links der alten Indifferenzkurve verläuft, sobald sie ein höheres Nutzenniveau bedeutet, sind die Präferenzen lokal nicht gesättigt. In dem linken Beispiel soll Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_1<U_2 }
gelten. Ausgehend vom Punkt x bringt der Punkt y ein höheres Nutzenniveau, da es auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_2 }
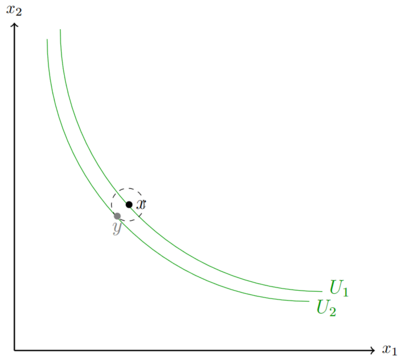
liegt. Auch in dem rechten Beispiel soll Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_1<U_2 }
gelten. Erneut existiert ausgehend vom Punkt x ein Punkt y in der Nähe, der ein höheres Nutzenniveau bedeutet. Auch im rechten Beispiel ist die Annahme der lokal nicht gesättigten Präferenzen nicht verletzt, obwohl ein geringeres Konsumniveau einen höheren Nutzen bedeutet. Informal bedeutet die Annahme der lokalen nicht Sättigung "Irgendwo in der Nähre ist es besser".
Monotonie
Monotonie: Wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_D > x_A }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_D \geq y_A }
, dann muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle D \backsim A }
gelten.
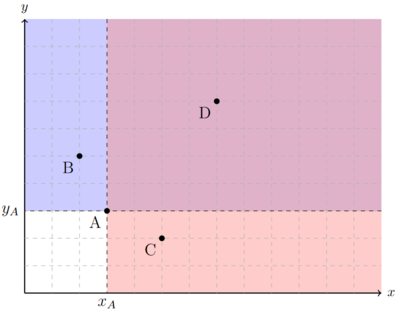
Die Monotonie besagt "Mehr ist besser". Sobald ein Konsumgüterbündel von einem der Güter mehr und von dem anderen mindestens gleich viel beinhaltet, muss dieses präferiert werden. Dies kann grafisch dargestellt werden. Angenommen die zu betrachtenden Konsumgüterbündel bestehen aus einer Menge des Gutes x und des Gutes y. Im Bündel A besitzt der Konsument eine Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_a }
und eine Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_A }
. Neben A stehen noch die Bündel B, C und D zur Auswahl, die der Konsument ausgehend von A bewerten soll. Die Monotonie Annahme sagt aus, dass sobald der Konsument in einem neuen Bündel mehr von dem Gut x konsumiert und mindestens genauso viel von y, er dieses neue Bündel präferieren muss. Mehr von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_A }
bedeutet der neue Punkt liegt im Koordinatensystem rechts davon (rote Fläche). Mindestens genauso viel als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_A }
bedeutet genau Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y_A }
oder oberhalb (blaue Fläche). Die Schnittmenge erfüllt beide Bedingungen (lilane Fläche). Jedes Bündel, das in der lilanen Fläche liegt, muss gegenüber A präferiert werden. Über jedes andere Bündel lässt sich keine Aussage treffen, ob eben dieses gegenüber A präferiert wird. In der Abbildung unten sind Bündel B und C zwei, bei denen nicht genau gesagt werden kann, ob ein Konsument diese gegenüber präferiert oder nicht. Bündel B verfügt über weniger x und Bündel C über weniger y als Bündel A.
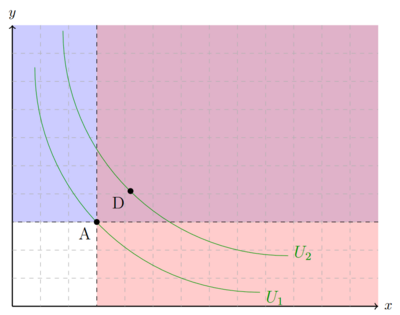
In der rechten Abbildung sind Indiffernzkurven eingezeichnet. Jeder Punkt in dem Koordinatensystem liegt auf einer Indifferenzkurve. Punkt A liegt auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_1 }
und Punkt D liegt auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_2 }
. Gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_2>U_1 }
ist die Monotonie Annahme nicht verletzt, gilt jedoch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_1>u_2 }
, ist die Annahme verletzt. Es ist offensichtlich, dass die Monotonie ein Spezialfall der lokalen Nict Sättigung darstellt. Bei der lokalen Nicht Sättigung reicht es, dass Bündel irgendwo in der Nähe besser bewertet werden. Bei der Monotonie wird festgehalten, wo diese "besseren" Bündel liegen dürfen. Das rechte Beispiel der lokalen Nicht Sättigung verletzt beispielsweise die Annahme der lokalen Nicht Sättigung nicht, jedoch die Annahme der Monotonie. Ein höheres Nutzenniveau kann in dem Beispiel überall außerhalb der lilanen Fläche gefunden werden.
MC Fragen