Budgetrestriktion und Budgetgerade

Definition

Die Budgetgerade bildet die Kombination aller möglichen Güterbündeln ab, bei denen die ausgegebene Geldsumme gleich dem Einkommen ist.

Konsumausgaben

Die Konsumausgaben für ein beliebiges Gut X stellen sich aus der konsumierten Mengen für dieses Gut und seinem Preis zusammen. Konsumausgaben von x${\textstyle =p_{x}*x}$.
Um die gesamten Konsumausgaben zu erlangen, muss über die Konsumausgaben der einzelnen Güter aufsummiert werden:
$C=\sum _{i}^{N}p_{i}*X_{i}$
In unseren Beispielen begrenzen wir uns häufig auf ein Zweigütermodell, sodass die Konsumausgaben wie folgt aussehen:

${\textstyle Konsumausgaben=p_{1}x_{1}+p_{2}x_{2}}$

Budgetrestriktion

Es steht ein begrenztes Budget E zur Verfügung, das maximal ausgeben werden kann. Der Konsum unterhalb dieses Budgets ist möglich, oberhalb dieses Budgets kann jedoch nicht konsumiert werden, da dies außerhalb der Budgetmöglichkeiten liegt. Die Konsumausgaben müssen daher geringer oder gleich dem Budget sein:
${\textstyle p_{1}x_{1}+p_{2}x_{2}}$≤${\textstyle E}$

Budgetgerade

Die Budgetrestriktion lässt sich in ein Diagramm zeichnen. Hierfür muss die Budgetrestriktion mit der Hilfe von Äquivalenzumformungen nach der Variablen umgestellt werden, die auf der vertikalen Achse abgebildet werden soll. Dabei wird Gleichheit angenommen, da die Budgetgerade alle Güterbündel darstellt, die gleich dem Einkommen E sind.
${\textstyle p_{1}x_{1}+p_{2}x_{2}=E}$ |${\textstyle -p_{1}x_{1}}$
${\textstyle p_{2}x_{2}=E-P_{1}x_{1}}$ | ${\textstyle :p_{2}}$
${\textstyle x_{2}={\frac {E}{p_{2}}}-{\frac {p_{1}}{p_{2}}}}$
Grafisch lässt sich die Budgetgerade dann wie folgt darstellen:



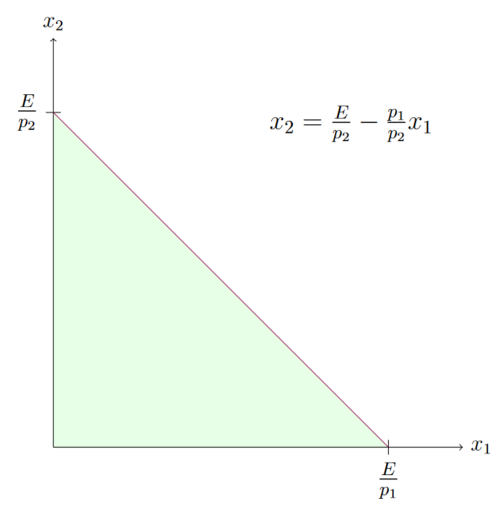
Auf der Geraden selbst wird das Budget vollständig ausgegeben. In der grün markierten Fläche wird unterhalb des Budgetmaximums konsumiert. Oberhalb der Budgetgeraden ist ein Konsum mit dem gegebenen Budget E nicht möglich. Die Achsenabschnitte der Budgetgerade beschreiben die Güterbündel, bei denen ausschließlich eines der Güter konsumiert wird.

Veränderung der Budgetgeraden

Es gibt zwei Möglichkeiten weshalb sich die Budgetgerade in einfachen Modell verändern könnte. Der Erste Grund ist die Veränderung von Preisen und der zweite Grund die Veränderung vom Budget E.

Veränderung der Preise
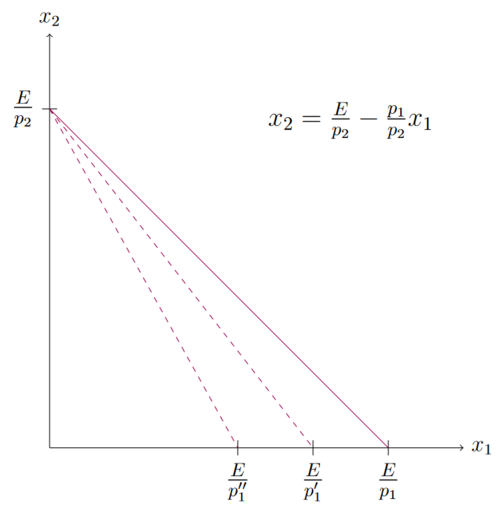
Wie sich die Budgetgerade verändert wenn sich die Preise verändern lässt sich sehr gut in den Achsenabschnitten sehen. Die Achsenabschnitte stellen den maximalen Konsum eines Guts bei gleichzeitigem Nichtkonsum des anderen Guts dar. Eine Preisänderung von Gut x1 verändert dabei nur den Achsenabschnitt auf der X-Achse. Der Achsenabschnitt auf der Y-Achse bleibt identisch, da sich der Preis von Gut x2 nicht verändert hat. Wenn sich nur der Preis eines Gutes verändert, führt dies zu einer Drehung der Budgetgeraden. In der Abbildung gilt $p''>p'>p$



Veränderung des Budgets
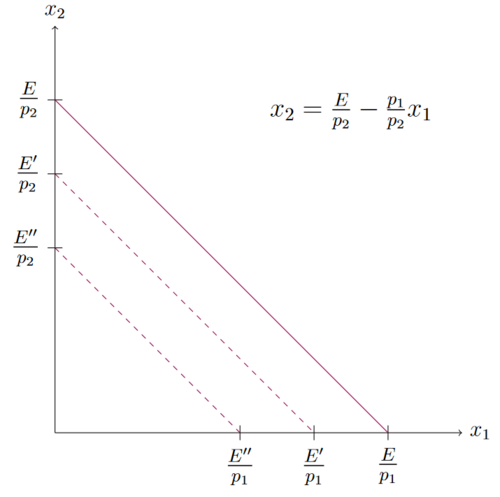
Wie sich die Budgetgerade bei veränderten Budget verändert lässt sich am besten in der Geradengleichung sehen ${\textstyle x_{2}={\frac {E}{p_{2}}}-{\frac {p_{1}}{p_{2}}}}$. Das veränderte Budget hat keinen Einfluss auf die Steigung der Budgetgeraden, lediglich auf die Achsenabschnitte. Je kleiner das Budget ist, desto weiter wird die Budgetgerade parallel zum Ursprung verschoben. In der Abbildung gilt ${\textstyle E>E'>E''}$.

MC Fragen

Wie groß ist das Budget und der Preis $p_{1}$ der Budgetgeraden, die bei einem Preis von ${\textstyle p_{2}=6}$ durch die Konsumpunkte ${\textstyle (x_{1},x_{2})=(2,8)}$ und ${\textstyle (x_{1},x_{2})=(4,4)}$ verläuft?

Der Preis $p_{1}$ lautet

Das Budget lautet

Welche der folgenden Konsumpunkte ist mit der Budgetgeraden ${\textstyle 2x+5y=12}$ nicht realisierbar?

	(x; y)=(0,75; 2)
	(x; y)=(6; 0)
	(x; y)=(6; 0,25)
	(x; y)=(3; 1)

Angenommen ${\textstyle x_{2}}$ befindet sich auf der Ordinate und ${\textstyle x_{1}}$ auf der Abszisse. Wie lautet die Budgetgerade mit den Preisen ${\textstyle p_{1}=6}$ und ${\textstyle p_{2}=7}$, die durch den Punkt ${\textstyle (x_{1},x_{2})=(1,2)}$ verläuft?

	${\textstyle x_{2}={\frac {7}{20}}-{\frac {6}{7}}x_{1}}$
	${\textstyle x_{2}={\frac {20}{7}}-{\frac {6}{7}}x_{1}}$
	${\textstyle x_{2}={\frac {20}{7}}-{\frac {7}{6}}x_{1}}$
	${\textstyle x_{2}={\frac {20}{7}}+{\frac {7}{6}}x_{1}}$