Einkommens-Konsumkurve: Unterschied zwischen den Versionen
Lobin (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| (11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
<math> E(x_1)=E(x_2) </math> <br> | <math> E(x_1)=E(x_2) </math> <br> | ||
Das Umstellen der Gleichung nach <math> x_2 </math> ergibt die Funktionsgleichung der Einkommens-Konsumkurve. <br> | Das Umstellen der Gleichung nach <math> x_2 </math> ergibt die Funktionsgleichung der Einkommens-Konsumkurve. <br> | ||
| − | ''Beispiel:'' Angenommen beide Güter | + | ''Beispiel:'' Angenommen für beide Güter liegen [[Güterarten|homothetische Präferenzen]]vor, daher sind die Gleichungen der Engelkurven mit <math> E(x_1)=ax_1 </math> und <math> E(x_2)=bx_2 </math> beschrieben. <br> |
Es ergibt sich <math> ax_1=bx_2 </math> und nach umstellen <br> | Es ergibt sich <math> ax_1=bx_2 </math> und nach umstellen <br> | ||
<math> x_2(x_1)=\frac{a}{b}x_1 </math> | <math> x_2(x_1)=\frac{a}{b}x_1 </math> | ||
==Inferiores Gut und Normales Gut== | ==Inferiores Gut und Normales Gut== | ||
| − | Die Nachfrage eines [[Güterarten| | + | Die Nachfrage eines [[Güterarten|normalen Gutes]] steigt, wenn das Einkommen steigt und hingegen sinkt die Nachfrage nach einem inferioren Gut. Die Veränderung der numerischen Werte des Konsums der beiden Güter zeigt, welcher der beiden Güterarten vorliegen. Sinkt der Wert bei immer größeren Einkommen, handelt es sich um ein inferiores Gut. Steigen die Werte ist das entsprechende Gut ein normales Gut. <br> |
[[Datei:EinkommenKonsumKurve2.png|400px|rahmenlos]] <br> | [[Datei:EinkommenKonsumKurve2.png|400px|rahmenlos]] <br> | ||
<br clear=all> | <br clear=all> | ||
| − | In dem abgebildeten Beispiel steigt die Nachfrage nach dem Gut <math> x_1 </math>, wenn auch das Budget steigt. Bei Gut <math> x_1 </math> handelt es sich demnach um ein normales Gut. Die Nachfrage nach Gut <math> x_2 </math> sinkt jedoch, daher handelt es sich um ein inferiores Gut. <br> | + | In dem abgebildeten Beispiel steigt die Nachfrage nach dem Gut <math> x_1 </math>, wenn auch das Budget steigt. Bei Gut <math> x_1 </math> handelt es sich demnach um ein normales Gut. Die Nachfrage nach Gut <math> x_2 </math> sinkt jedoch, daher handelt es sich bei Gut 2 um ein inferiores Gut. <br> |
| − | + | Allgemein gilt: sinkt die EKK, ist eines der Güter ein inferiores Gut. <br> | |
| − | + | Eines der Güter ist inferior, wenn <math> \frac{\part x^*_2(x_1^*)}{\part x_1}<0 </math> <br> | |
| − | + | Beide Güter sind normal, wenn <math> \frac{\part x^*_2(x_1^*)}{\part x_1}>0 </math> | |
| − | |||
| − | <math> \frac{\part | ||
| − | |||
| − | |||
| − | <math> | ||
| − | |||
==MC Fragen== | ==MC Fragen== | ||
| Zeile 49: | Zeile 43: | ||
- ist positiv geneigt,da eine Preisänderung des anderen Gutes zu einer gesteigerten Nachfrage führt | - ist positiv geneigt,da eine Preisänderung des anderen Gutes zu einer gesteigerten Nachfrage führt | ||
- ist positiv geneigt, da ein höheres Einkommen die Nachfrage nach beiden Gütern senkt | - ist positiv geneigt, da ein höheres Einkommen die Nachfrage nach beiden Gütern senkt | ||
| − | + | + | + (die EKK kann grafisch nicht dargestellt werden) |
- ist negativ geneigt,da eine Preisänderung des anderen Gutes zu einer gesteigerten Nachfrage führt | - ist negativ geneigt,da eine Preisänderung des anderen Gutes zu einer gesteigerten Nachfrage führt | ||
</quiz> | </quiz> | ||
<quiz display=simple shuffleanswers=true> | <quiz display=simple shuffleanswers=true> | ||
| − | {Eine Engelkurve für | + | {Eine Engelkurve für zwei Güter muss eine positive Steigung aufweisen, wenn... |
|type="()"} | |type="()"} | ||
| − | - | + | - ... die Nachfrage nach beiden Güter steigt, wenn der Preis steigt |
| − | - | + | - ... die Nachfrage nach beiden Güter sinkt, wenn der Preis steigt. |
| − | + | + ... die Nachfrage nach beiden Gütern steigt, wenn das Einkokmmen steigt. | |
| − | - | + | - ... die Nachfrage nach beiden Gütern sinkt, wenn das Einkommen steigt. |
</quiz> | </quiz> | ||
Aktuelle Version vom 10. Oktober 2023, 18:53 Uhr
Definition
Die Einkommens-Konsumkurve, auch Einkommens-Expansionspfad, ist die Verbindungslinie aller optimalen Verbrauchspläne bei variierendem Einkommen und konstanten Güterpreisen. Sie beschreibt, wie sich das optimale Konsumgüterbündel verändert, wenn ceteris paribus das Einkommen steigt oder sinkt.
Einkommensänderung
Wenn sich das Budget (beziehungsweise Einkommen) ändert, hat dies keinen Einfluss auf die Steigung der Budgetgerade, lediglich die Achsenabschnitte verschieben sich parallel. Je kleiner das Budget ist, desto weiter wird die Budgetgerade parallel Richtung Ursprung verschoben. In der Abbildung gilt .
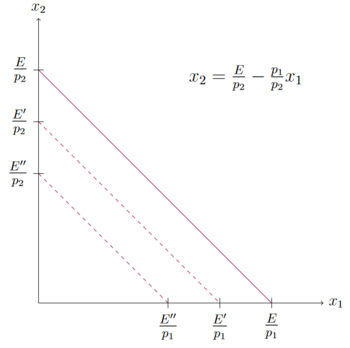
Die Einkommens-Konsumkurve
Die Einkommens-Konsumkurve (EKK) bildet die optimale Nachfrage für alle Einkommen ab. Verändert sich das Budget, ist das alte Konsumgüterbündel nicht mehr optimal. Bei einem höheren Budget, wird dieses nicht vollständig ausgegeben im alten Konsumgüterbündel und die zugehörige Indifferenzkurve schneidet die neue Budgetgerade in der Regel. Bei einem verringertem Budget, liegt das alte Konsumbündel außerhalb der Konsummöglichkeiten (oberhalb der Budgetgerade). In beiden Fällen lässt sich ein neuer Tangentialpunkt finden. Die EKK verbindet grafisch alle Tangentialpunkte der einzelnen Budgetgeraden und den Indifferenzkurven miteinander. Es ergibt sich eine vom Einkommen unabhängige Funktion . Der Verlauf der EKK bestimmt, welche mathematischen Eigenschaften die Engelkurven der einzelnen Güter haben und welche Güterarten vorliegen.
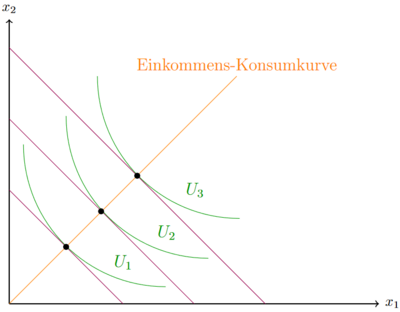
Rechnerisch werden die Funktionen der Engelkurven beider Güter gleichgesetzt.
Das Umstellen der Gleichung nach ergibt die Funktionsgleichung der Einkommens-Konsumkurve.
Beispiel: Angenommen für beide Güter liegen homothetische Präferenzenvor, daher sind die Gleichungen der Engelkurven mit und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E(x_2)=bx_2 }
beschrieben.
Es ergibt sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle ax_1=bx_2 }
und nach umstellen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2(x_1)=\frac{a}{b}x_1 }
Inferiores Gut und Normales Gut
Die Nachfrage eines normalen Gutes steigt, wenn das Einkommen steigt und hingegen sinkt die Nachfrage nach einem inferioren Gut. Die Veränderung der numerischen Werte des Konsums der beiden Güter zeigt, welcher der beiden Güterarten vorliegen. Sinkt der Wert bei immer größeren Einkommen, handelt es sich um ein inferiores Gut. Steigen die Werte ist das entsprechende Gut ein normales Gut.
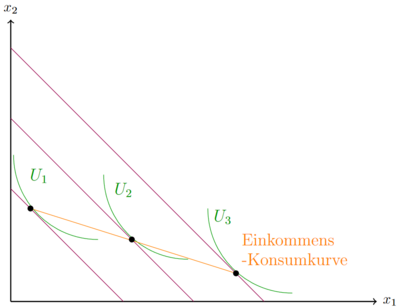
In dem abgebildeten Beispiel steigt die Nachfrage nach dem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
, wenn auch das Budget steigt. Bei Gut handelt es sich demnach um ein normales Gut. Die Nachfrage nach Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
sinkt jedoch, daher handelt es sich bei Gut 2 um ein inferiores Gut.
Allgemein gilt: sinkt die EKK, ist eines der Güter ein inferiores Gut.
Eines der Güter ist inferior, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part x^*_2(x_1^*)}{\part x_1}<0 }
Beide Güter sind normal, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part x^*_2(x_1^*)}{\part x_1}>0 }
MC Fragen
