Substitutionseffekt, Einkommenseffekt und Gesamteffekt: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Eine Preisänderung wirkt sich auf die Konsumentscheidung aus. Hierbei lässt sich der Gesamteffekt, die Veränderung der Konsumentscheidung, in zwei Effekte aufgliedern: In den Substitutionseffekt und den Einkommenseffekt. | + | Eine Preisänderung wirkt sich auf die Konsumentscheidung aus. Hierbei lässt sich der Gesamteffekt, die Veränderung der Konsumentscheidung, in zwei Effekte aufgliedern: In den Substitutionseffekt und den Einkommenseffekt. Dies ist in vielen Situationen sehr hilfreich, etwa wenn bei wirtschaftspolitischen Entscheidungen nur die Änderung der relativen Preise (etwa bei Änderungen der Energiepreise) zum Tragen kommen soll, nicht aber der Kaufkrafteffekt der Preisänderung (den wir hier im Folgenden als Einkommenseffekt bezeichnen wollen). |
==Der Substitutionseffekt== | ==Der Substitutionseffekt== | ||
| − | Der | + | Der Substitutionseffekt umfasst die Auswirkungen, die alleinig die Preisveränderung mit sich führt und hält dabei das reale Einkommen ([[Substitutionseffekt, Einkommenseffekt und Gesamteffekt#Nach Slutsky|Nach Slutsky]]) oder den Nutzen ([[Substitutionseffekt, Einkommenseffekt und Gesamteffekt#Nach Hicks|Nach Hicks]]) konstant. Der Substitutionseffekt besteht darin, dass Konsumenten das relativ teurer gewordene Gut mit dem relativ günstiger gewordenen Gut substituieren. |
<br> | <br> | ||
| Zeile 11: | Zeile 11: | ||
Der Einkommenseffekt umfasst die Änderung des Konsumverhaltens aufgrund der Veränderung der realen Kaufkraft. Hierbei bleiben die relativen Preise konstant. | Der Einkommenseffekt umfasst die Änderung des Konsumverhaltens aufgrund der Veränderung der realen Kaufkraft. Hierbei bleiben die relativen Preise konstant. | ||
<br> <br> | <br> <br> | ||
| − | Im ''Beispiel'' bedeutet das, dass durch die Veränderung des Lebensmittelpreises an Kaufkraft dazugewonnen wird. Da Lebensmittel günstiger werden kann der Konsument von seinem nominal | + | Im ''Beispiel'' bedeutet das, dass durch die Veränderung des Lebensmittelpreises an Kaufkraft dazugewonnen wird. Da Lebensmittel günstiger werden kann der Konsument von seinem nominal gleichbleibenden Budget real mehr kaufen. Um den Effekt, der sich verändernden Preise zu ignorieren und lediglich den Effekt durch das Einkommen zu betrachten, wird das Preisverhältnis auf dem neuen Niveau konstant gehalten und sich der Sprung vom alten Punkt mit konstanter Kaufkraft ([[Substitutionseffekt, Einkommenseffekt und Gesamteffekt#Nach Slutsky|Nach Slutsky]]) oder vom konstanten alten Nutzen ([[Substitutionseffekt, Einkommenseffekt und Gesamteffekt#Nach Hicks|Nach Hicks]]) zum neuen optimalen Konsumpunkt angeschaut. Ob der Einkommenseffekt positiv oder negativ ist, hängt damit zusammen, welche Art der Güter vorliegen. |
==Der Gesamteffekt== | ==Der Gesamteffekt== | ||
| Zeile 19: | Zeile 19: | ||
==Nach Slutsky== | ==Nach Slutsky== | ||
| − | Um die Aufgliederung des Gesamteffekts nach Slutsky zu betrachten soll uns ein | + | Um die Aufgliederung des Gesamteffekts nach Slutsky zu betrachten, soll uns ein Beispiel mit einem Gut F und einem Gut C dienen. In unserem Beispiel wird das Gut F günstiger, die Budgetgerade dreht sich also nach außen. Vorher lag der optimaler Konsumpunkt in A. Slutsky schaut sich in der Aufgliederung des '''Substitutionseffekts''' die neue Budgetgerade an, um das neue Preisverhältnis (den Effekt den die neuen Preise haben) einzubeziehen. Hierbei verschiebt er nun die neue Budgetgerade parallel nach unten, die Steigung, also das neue Preisverhältnis verändert sich dabei nicht. Diese fiktive Budgetgerade wird durch den alten Konsumpunkt gezogen, da wir nun in der Budgetgeraden ein Budget haben, das die reale Kaufkraft konstant hält. Die neue Budgetgerade führt nun durch den Punkt A. Der Punkt A ist nun nicht mehr optimal. Es lässt sich ein neuer Punkt D finden, der auf einer Indifferenzkurve liegt, die fiktive Budgetgerade tangiert. Der Sprung von A zu D ist der Substitutionseffekt. In der Differenz der beiden Konsumniveaus spielen nur die veränderten Preise und nicht das veränderte Einkommen eine Rolle. <br> |
Mathematisch lässt sich das wie folgt berechnen: <math display="inline"> SE_{F}=Q_{F}(p_{F}',p_{C}, E')-Q_{F}(p_{F},p_{C}, E) </math>, wobei <math display="inline"> p_{F}'</math> der neue Preis von F ist und <math display="inline"> E'</math> das fiktive neue Einkommen, das die Budgetgerade durch den Punkt A führen lässt. <br> | Mathematisch lässt sich das wie folgt berechnen: <math display="inline"> SE_{F}=Q_{F}(p_{F}',p_{C}, E')-Q_{F}(p_{F},p_{C}, E) </math>, wobei <math display="inline"> p_{F}'</math> der neue Preis von F ist und <math display="inline"> E'</math> das fiktive neue Einkommen, das die Budgetgerade durch den Punkt A führen lässt. <br> | ||
<br> | <br> | ||
| Zeile 27: | Zeile 27: | ||
<br> | <br> | ||
<br clear=all> | <br clear=all> | ||
| − | Um den Effekt, den das veränderte Einkommen hat separat zu betrachten, nimmt Slutsky den Punkt D und schaut sich den Sprung zum neuen optimalen Konsumpunkt mit dem neuen Einkommen und dem neuen Preisverhältnis an (Punkt B). Da im Punkt D bereits auch das neue Preisverhältnis steckt, haben wir so den Effekt, den die | + | Um den Effekt, den das veränderte Einkommen hat, separat zu betrachten, nimmt Slutsky den Punkt D und schaut sich den Sprung zum neuen optimalen Konsumpunkt mit dem neuen Einkommen und dem neuen Preisverhältnis an (Punkt B). Da im Punkt D bereits auch das neue Preisverhältnis steckt, haben wir so den Effekt, den die Einkommensänderung mit sich führt. <br> |
Mathematisch lässt sich der '''Einkommenseffekt''' wie folgt berechnen: <math display="inline"> EE_{F}=Q_{F}(p_{F}',p_{C}, E)-Q_{F}(p_{F}',p_{C}, E') </math>. | Mathematisch lässt sich der '''Einkommenseffekt''' wie folgt berechnen: <math display="inline"> EE_{F}=Q_{F}(p_{F}',p_{C}, E)-Q_{F}(p_{F}',p_{C}, E') </math>. | ||
<br> | <br> | ||
| Zeile 39: | Zeile 39: | ||
==Nach Hicks== | ==Nach Hicks== | ||
| − | Als Unterscheidung zu [[Substitutionseffekt, Einkommenseffekt und Gesamteffekt#Nach Slutsky|Slutsky]] hält Hicks nicht das Einkommen konstant, sondern den Nutzen um den Substitutionseffekt herauszufiltern. Dabei nimmt Hicks das neue Preisverhältnis in Form der Steigung der neuen Budgetgeraden und | + | Als Unterscheidung zu [[Substitutionseffekt, Einkommenseffekt und Gesamteffekt#Nach Slutsky|Slutsky]] hält Hicks nicht das Einkommen konstant, sondern den Nutzen, um den Substitutionseffekt herauszufiltern. Dabei nimmt Hicks das neue Preisverhältnis in Form der Steigung der neuen Budgetgeraden und verschiebt die parallel, bis die Indifferenzkurve des alten Konsumpunkts A tangiert wird. Die Differenz zwischen dem darauf resultierenden Güterbündel (Punkt D) und dem alten optimalen Bündel (Punkt A) ist der '''Substitutionseffekt''' nach Hicks. <br> |
<br> | <br> | ||
[[Datei:Hicks4.png|300px|rahmenlos]] | [[Datei:Hicks4.png|300px|rahmenlos]] | ||
| Zeile 70: | Zeile 70: | ||
|} | |} | ||
<br> | <br> | ||
| − | Es ist deutlich zu sehen, dass der Substitutionseffekt immer für das Gut positiv ist, dass relativ zum anderen Gut günstiger geworden und für das Gut negativ, das relativ zum anderen Gut teurer geworden ist. Die Nachfrage nach [[Normalen Güter]] steigt im | + | Es ist deutlich zu sehen, dass der Substitutionseffekt immer für das Gut positiv ist, dass relativ zum anderen Gut günstiger geworden und für das Gut negativ, das relativ zum anderen Gut teurer geworden ist. Die Nachfrage nach [[Güterarten#Einkommensänderungen#Normale Güter|Normalen Güter]] steigt im steigenden Einkommen und sinkt bei [[Güterarten#Einkommensänderungen#Inferiore Güter|inferioren Gütern]]. Sind die beiden Effekte gegenläufig, so ist der Gesamteffekt nicht eindeutig. Sollte X ein [[Güterarten#Preisänderungen#Giffen Güter|Giffen Gut]] sein, so ist bei einer Preiserhöhung von Gut X jedoch der EE betragsmäßig größer als der SE und der Gesamteffekt daher positiv. |
==MC Fragen== | ==MC Fragen== | ||
| Zeile 84: | Zeile 84: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { In einem zwei Gütermodell gebe es ein Gut X und ein Gut Y. Die Nachfrage nach Gut X sei gegeben durch folgende Funktion: <math display="inline"> X=\frac{E}{p_{x}} </math>. Bei einem Preis von <math display="inline"> p_{x}=2 </math> und einem Preis von <math display="inline"> p_{y}=10 </math> werden 15 Einheiten von X und | + | { In einem zwei Gütermodell gebe es ein Gut X und ein Gut Y. Die Nachfrage nach Gut X sei gegeben durch folgende Funktion: <math display="inline"> X=\frac{0,5*E}{p_{x}} </math>. Bei einem Preis von <math display="inline"> p_{x}=2 </math> und einem Preis von <math display="inline"> p_{y}=10 </math> werden 15 Einheiten von X und 3 Einheiten von Y nachgefragt. |
|type="{}"} | |type="{}"} | ||
| − | Wie groß ist der Substitutionseffekt nach Slutsky, wenn <math display="inline"> p_{x} </math> auf 4 steigt? { - | + | Wie groß ist der Substitutionseffekt für x nach Slutsky, wenn <math display="inline"> p_{x} </math> auf 4 steigt? { -3,75|-3.75 } |
</quiz> | </quiz> | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { In einem zwei Gütermodell gebe es ein Gut X und ein Gut Y. Die Nachfrage nach Gut X sei gegeben durch folgende Funktion: <math display="inline"> X=\frac{E}{p_{x}} </math>. Bei einem Preis von <math display="inline"> p_{x}=2 </math> und einem Preis von <math display="inline"> p_{y}=10 </math> werden 15 Einheiten von X und | + | { In einem zwei Gütermodell gebe es ein Gut X und ein Gut Y. Die Nachfrage nach Gut X sei gegeben durch folgende Funktion: <math display="inline"> X=\frac{0,5*E}{p_{x}} </math>. Bei einem Preis von <math display="inline"> p_{x}=2 </math> und einem Preis von <math display="inline"> p_{y}=10 </math> werden 15 Einheiten von X und 3 Einheiten von Y nachgefragt. |
|type="{}"} | |type="{}"} | ||
| − | Wie groß ist der Einkommenseffekt nach Slutsky, wenn <math display="inline"> p_{x} </math> auf 4 steigt? { - | + | Wie groß ist der Einkommenseffekt für x nach Slutsky, wenn <math display="inline"> p_{x} </math> auf 4 steigt? { -3,75|-3.75 } |
</quiz> | </quiz> | ||
Aktuelle Version vom 11. Oktober 2023, 16:26 Uhr
Eine Preisänderung wirkt sich auf die Konsumentscheidung aus. Hierbei lässt sich der Gesamteffekt, die Veränderung der Konsumentscheidung, in zwei Effekte aufgliedern: In den Substitutionseffekt und den Einkommenseffekt. Dies ist in vielen Situationen sehr hilfreich, etwa wenn bei wirtschaftspolitischen Entscheidungen nur die Änderung der relativen Preise (etwa bei Änderungen der Energiepreise) zum Tragen kommen soll, nicht aber der Kaufkrafteffekt der Preisänderung (den wir hier im Folgenden als Einkommenseffekt bezeichnen wollen).
Der Substitutionseffekt
Der Substitutionseffekt umfasst die Auswirkungen, die alleinig die Preisveränderung mit sich führt und hält dabei das reale Einkommen (Nach Slutsky) oder den Nutzen (Nach Hicks) konstant. Der Substitutionseffekt besteht darin, dass Konsumenten das relativ teurer gewordene Gut mit dem relativ günstiger gewordenen Gut substituieren.
Beispiel: Ein Lebensmittel kostet 6€ und ein Kleidungsstück 2€. Aktuell gibt ein Konsument sein Budget vollständig aus. Würde der Konsument ein Lebensmittel mehr konsumieren wollen, so müsste er auf drei Kleidungsstücke verzichten.
Kommt es nun zu einer Preissenkung der Lebensmittel, sodass eine Einheit nur noch 4€ kostet, so müsste der Konsument nur noch auf zwei Kleidungsstücke verzichten. Relativ zu Lebensmitteln sind die Kleidungsstücke also günstiger geworden und relativ zu den Lebensmitteln die Kleidungsstücke teurer. Was zu einem höheren Konsum von Lebensmittel führen kann.
Der Einkommenseffekt
Der Einkommenseffekt umfasst die Änderung des Konsumverhaltens aufgrund der Veränderung der realen Kaufkraft. Hierbei bleiben die relativen Preise konstant.
Im Beispiel bedeutet das, dass durch die Veränderung des Lebensmittelpreises an Kaufkraft dazugewonnen wird. Da Lebensmittel günstiger werden kann der Konsument von seinem nominal gleichbleibenden Budget real mehr kaufen. Um den Effekt, der sich verändernden Preise zu ignorieren und lediglich den Effekt durch das Einkommen zu betrachten, wird das Preisverhältnis auf dem neuen Niveau konstant gehalten und sich der Sprung vom alten Punkt mit konstanter Kaufkraft (Nach Slutsky) oder vom konstanten alten Nutzen (Nach Hicks) zum neuen optimalen Konsumpunkt angeschaut. Ob der Einkommenseffekt positiv oder negativ ist, hängt damit zusammen, welche Art der Güter vorliegen.
Der Gesamteffekt
Der Gesamteffekt ist die Summe aus dem Substitutionseffekt und dem Einkommenseffekt (GE=SE+EE)
Der Gesamteffekt lässt sich als verändertes Konsumverhalten beobachten. Er beschreibt den Sprung vom optimalen Konsumpunkt vor der Preisveränderung zum optimalen Konsumpunkt nach der Preisänderung.
Nach Slutsky
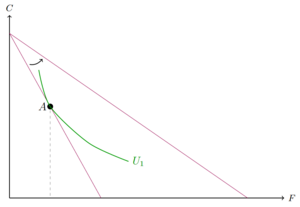
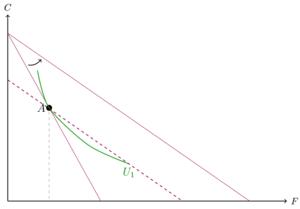
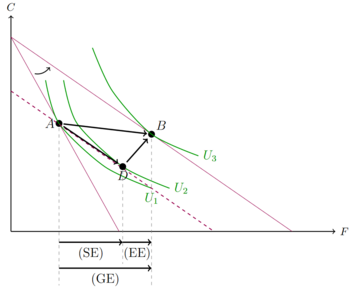
Um die Aufgliederung des Gesamteffekts nach Slutsky zu betrachten, soll uns ein Beispiel mit einem Gut F und einem Gut C dienen. In unserem Beispiel wird das Gut F günstiger, die Budgetgerade dreht sich also nach außen. Vorher lag der optimaler Konsumpunkt in A. Slutsky schaut sich in der Aufgliederung des Substitutionseffekts die neue Budgetgerade an, um das neue Preisverhältnis (den Effekt den die neuen Preise haben) einzubeziehen. Hierbei verschiebt er nun die neue Budgetgerade parallel nach unten, die Steigung, also das neue Preisverhältnis verändert sich dabei nicht. Diese fiktive Budgetgerade wird durch den alten Konsumpunkt gezogen, da wir nun in der Budgetgeraden ein Budget haben, das die reale Kaufkraft konstant hält. Die neue Budgetgerade führt nun durch den Punkt A. Der Punkt A ist nun nicht mehr optimal. Es lässt sich ein neuer Punkt D finden, der auf einer Indifferenzkurve liegt, die fiktive Budgetgerade tangiert. Der Sprung von A zu D ist der Substitutionseffekt. In der Differenz der beiden Konsumniveaus spielen nur die veränderten Preise und nicht das veränderte Einkommen eine Rolle.
Mathematisch lässt sich das wie folgt berechnen: , wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{F}'}
der neue Preis von F ist und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle E'}
das fiktive neue Einkommen, das die Budgetgerade durch den Punkt A führen lässt.
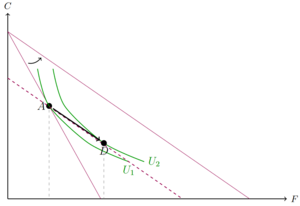
Um den Effekt, den das veränderte Einkommen hat, separat zu betrachten, nimmt Slutsky den Punkt D und schaut sich den Sprung zum neuen optimalen Konsumpunkt mit dem neuen Einkommen und dem neuen Preisverhältnis an (Punkt B). Da im Punkt D bereits auch das neue Preisverhältnis steckt, haben wir so den Effekt, den die Einkommensänderung mit sich führt.
Mathematisch lässt sich der Einkommenseffekt wie folgt berechnen: .
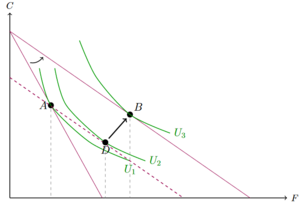
Der Gesamteffekt ist der Sprung von A zu B:
Nach Hicks
Als Unterscheidung zu Slutsky hält Hicks nicht das Einkommen konstant, sondern den Nutzen, um den Substitutionseffekt herauszufiltern. Dabei nimmt Hicks das neue Preisverhältnis in Form der Steigung der neuen Budgetgeraden und verschiebt die parallel, bis die Indifferenzkurve des alten Konsumpunkts A tangiert wird. Die Differenz zwischen dem darauf resultierenden Güterbündel (Punkt D) und dem alten optimalen Bündel (Punkt A) ist der Substitutionseffekt nach Hicks.
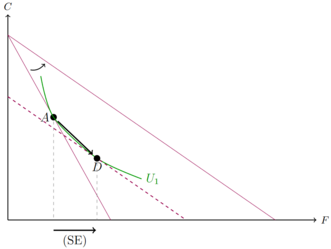
Um nun den Effekt herauszufiltern, den das Einkommen mit sich führt, nimmt Hicks den optimalen Punkt der fiktiven Bugetgerade mit dem neuen Preisverhältnis und vergleicht diesen mit dem neuen optimalen Konsumpunkt der tatsächlich neu entstandenen Budgetgerade. So wird das Preisverhältnis konstant gehalten und der Effekt ist lediglich durch die Veränderung des Einkommens bedingt, dem Einkommenseffekt:
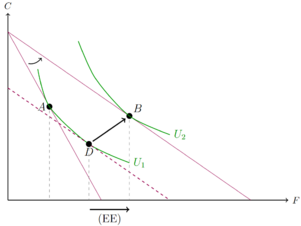
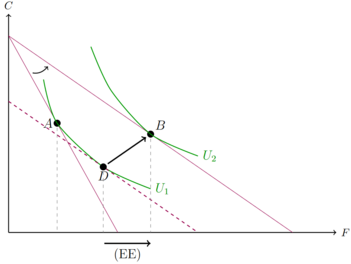
Auch hier ergeben die Summe der beiden Effekte den Gesamteffekt. Ungeachtet dessen welche der beiden Verfahren man nutzt, ist in beiden Fällen der Gesamteffekt gleich groß.
Richtung der Effekte
Um die Richtung der Effekte deuten zu können soll folgende Matrix dienen:
| X ist ein normales Gut | X ist ein inferiores Gut | |
|---|---|---|
| px↑ | SE: X↓, EE: X↓, GE: X↓ | SE: X↓, EE: X↑, GE: ? |
| py↑ | SE: X↑, EE: X↓, GE: ? | SE: X↑, EE: X↑, GE: X↑ |
Es ist deutlich zu sehen, dass der Substitutionseffekt immer für das Gut positiv ist, dass relativ zum anderen Gut günstiger geworden und für das Gut negativ, das relativ zum anderen Gut teurer geworden ist. Die Nachfrage nach Normalen Güter steigt im steigenden Einkommen und sinkt bei inferioren Gütern. Sind die beiden Effekte gegenläufig, so ist der Gesamteffekt nicht eindeutig. Sollte X ein Giffen Gut sein, so ist bei einer Preiserhöhung von Gut X jedoch der EE betragsmäßig größer als der SE und der Gesamteffekt daher positiv.
MC Fragen
