Monotone Transformation

Definition

Die monotone Transformation ist eine mathematische Operation, durch die Präferenzen einer Nutzenfunktion nicht verändert werden. Die monotone Transformation unterliegt der Annahme der ordinalen Nutzentheorie.

Monotone Transormationen

Die Nutzenfunktionen der Ordinalen Nutzentheorie bringen Güterkombinationen in einer Rangfolge. Jede mathematische Operation, die ausgehend der Nutzenfunktion, die Präferenzen nicht verändert, ist eine monotone Transformation.
Beispiel: In der Marktforschung werden Konsumentinnen und Konsumenten gefragt, wie ihnen verschiedene Tiefkühlpizzen schmecken. Hierbei sollen sie die Pizza auf einer Skala bewerten. Welche Pizza einer jeweiligen Person eine bessere Bewertung bekommt, muss losgelöst davon sein, ob die Skala bis 5 oder bis 10 geht.


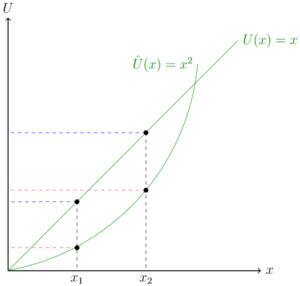
Die Grafik oben stellt eine monotone Transformation im univariaten Fall dar. Entscheidend ist, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } bei beiden Nutzenfunktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(x) } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x) } gegenüber Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } ein höheres Nutzenniveau bringt und daher bevorzugt wird.

Operationen

Die Monotone Transformation bezieht sich auch auf die gesamte Nutzenfunktion. Ist der Nutzen beispielsweise abhängig von zwei Variablen, müssen die mathematischen Operationen auf die gesamte $U(x_{1},x_{2})$ Funktion angewendet werden.
Beispiel: lautet die Nutzenfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(x_1,x_2)=x_1+x_2 } , spiegelt eine Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{U}(x_1,x_2)=2x_1+x_2 } nicht dieselben Präferenzen wider. Die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x_1,x_2)=2x_1+2x_2 } verändert die Präferenzen hingegen nicht und wäre somit eine monotone Transformation.

Addition und Subtraktion: Von einer Nutzenfunktion kann eine Zahl abgezogen oder zu ihr addiert werden, ohne die Präferenzen zu verändern. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x_1,x_2)=U(x_1,x_2)+b } bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x_1,x_2)=U(x_1,x_2)-b } mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b \in \mathbb{R}^+ }
Multiplikation und Division: Wird eine Nutzenfunktion mit einer positiven Zahl multipliziert oder dividiert, werden weiterhin dieselben Präferenzen abgebildet. Der oben genannte Fall mit der Skala ist ein Beispiel, bei dem die Präferenzen unverändert sind. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x_1,x_2)=U(x_1,x_2)*b } bzw. ${\hat {U}}(x_{1},x_{2})=U(x_{1},x_{2}):b$ mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b \in \mathbb{R}^+ }
Logarithmus: Wird der ln von einer Funktion gezogen, gilt dies auch als monotone Transformation. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x_1,x_2)=ln[U(x_1,x_2)] }
Potenz mit der Basis e: Die ganze Nutzenfunktion kann zu e hoch der Funktion umgeschrieben werden. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x_1,x_2)=e^{U(x_1,x_2)} }
Potenz und Wurzel: Eine Nutzenfunktion kann mit einer positiven Zahl potenziert werden oder von ihr eine positive Wurzel gezogen werden. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x_1,x_2)=[U(x_1,x_2)]^b } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x_1,x_2)=\sqrt[b]{U(x_1,x_2)} } mit $b\in \mathbb {R} ^{+}$

MC Fragen

Welche der Aussagen ist wahr?

	Monotone Transformationen verändern die Rangordnung von Präferenzen nicht und sind somit Teil der Ordinalen Nutzentheorie
	Monotone Transformationen verändern die Rangordnung von Präferenzen und sind somit Teil der Ordinalen Nutzentheorie
	Monotone Transformationen verändern die Rangordnung von Präferenzen nicht und sind somit Teil der Kardinalen Nutzentheorie
	Monotone Transformationen verändern die Rangordnung von Präferenzen und sind somit Teil der Kardinalen Nutzentheorie

Welche der folgenden Nutzenfunktionen stellen nicht die selben Präferenzen wie die folgende Nutzenfunktion dar: $U(x,y)=x^{2}{\sqrt {y}}$

	${\hat {U}}(x,y)=x^{2}{\sqrt {y}}+5$.
	${\hat {U}}(x,y)=2ln(x)+{\frac {1}{2}}ln(y)$.
	${\hat {U}}(x,y)=(1-x)+{\frac {1}{2}}y$.
	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{U}(x,y)=2x^{2} \sqrt{y} } .

"Monotone Transformationen von Nutzenfunktionen verändern die Präferenzen nicht, dennoch können sie verändern, wie Güter wahrgenommen werden. Aus perfekten Substituten können Imperfekte Substitute werden". Die Aussage ist

	Wahr
	Falsch