Nash Gleichgewicht

Das Nash Gleichgewicht ist die nach John Nash benannte Kombination von Strategien zweier Spieler, bei der kein Spieler einseitig den Anreiz hat abzuweichen.

Nash Gleichgewicht

Definition

Mathematisch werden Nash Gleichgewichte wie folgt definiert:
$(s_{1}^{*},s_{2}^{*})$ ist ein Nash Gleichgewicht, wenn $U_{1}(s_{1}^{*},s_{2}^{*})\geq U_{1}(s_{i},s_{2}^{*})$ und $U_{2}(s_{1}^{*},s_{2}^{*})\geq U_{2}(s_{1}^{*},s_{i})$ für $s_{i}\in S$.

In reinen Strategien

In einem gegebenen Gefangenendilemma ist das Nash Gleichgewicht NG=(Verrat, Verrat). Spieler 1 hat keinen Anreiz einseitig abzuweichen, wenn er allein durch seine Entscheidung zu keinem höheren Payoff gelangen kann. Da er nur bestimmen kann in welcher Zeile der Ausgang des Spiels liegen wird, muss geschaut werden, ob er ausgehend von der Entscheidung von Spieler 2 (Verrat) zu einem höheren Payoff gelangen kann. Wählt er statt Verrat doch Schweigen, hat er einen Payoff von -10, was geringer ist als -5.
Ist ein Ausgang kein Nash Gleichgewicht, wird dieser von rationalen Spielern in der Form nie erreicht, da immer ein einseitiger Anreiz zum Abweichen vorliegt.


Die Identifizierung eines Nash Gleichgewichts hängt stark mit der Idee der Beste Antwort zusammen.

In gemischten Strategien

Ein Spieler sollte seine gemischte Strategie so wählen, dass sein Nutzen maximal ist. Im Beispiel eines "Schere, Stein, Papier"-Spiels sollte er die Wahrscheinlichkeiten, mit denen er die jeweiligen reinen Strategien spielt, so wählen, dass der andere Spieler keine dominante Strategie besitzt. Der Nutzen eines Gewinns entspricht 1 und der Nutzen einer Niederlage 0. Die Payoffs ergeben, dass ein rationaler Spieler eine gemischte Strategie $\sigma =({\frac {1}{3}},{\frac {1}{3}},{\frac {1}{3}})$ spielen. Wenn Spieler 1 mit einer größeren Wahrscheinlichkeit Schere spielen würde, müsste Spieler 2 immer Papier spielen, damit sich sein erwarteter Payoff erhöht. Das führt wiederum dazu, dass Spieler 1 einen Anreiz hat abzuweichen. Nur bei $\sigma _{1}^{*}=({\frac {1}{3}},{\frac {1}{3}},{\frac {1}{3}})$ und $\sigma _{2}^{*}=({\frac {1}{3}},{\frac {1}{3}},{\frac {1}{3}})$ existiert in dem speziellen Anwendungsbeispiel kein Anreiz für einen der beiden Spieler abzuweichen. $(\sigma _{1}^{*},\sigma _{2}^{*})$ ist ein Nash Gleichgewicht in gemischten Strategien.

Beste Antwort

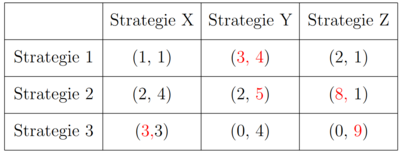
Die Beste Antwort ist ein Konzept, bei dem untersucht wird welche Strategie eines Spielers die Beste Antwort auf die Strategie eines anderen Spielers ist. Die Beste Antwort von Spieler 1 auf die Strategie X ist Strategie 3, da dort der Payoff in der Spalte am größten ist (Zur Erinnerung: Spieler 1 ist der Zeilenspieler und kann bestimmen in welcher Zeile der Ausgang liegen wird). Spieler 2 betrachtet, bei welcher Strategie sein Payoff (der zweitgenannte) in jeder Zeile am größten ist. Wäre der Payoff in mehreren Spalten gleich groß, gibt es mehrere Beste Antworten.
Die Payoffs von (Strategie 1, Strategie X) lauten (3, 3). Ist dies ein Nash Gleichgewicht? Immerhin ist die Strategie die Beste Antwort von Spieler 1 auf Strategie X. Tatsächlich hat Spieler 2 in (Strategie 1, Strategie X) einen Anreiz abzuweichen, denn wenn Spieler 1 Strategie 1 wählt, sollte Spieler 2 Strategie Z spielen. (Strategie1, Strategie Z) bietet für Spieler 1 wiederum den Anreiz auf Strategie 2 auszuweichen und so weiter. Nur der Ausgang, der für beide Spieler eine Beste Antwort bedeutet, hat keiner einen Anreiz abzuweichen. Fallen zwei Beste Antworten zusammen, ist der Ausgang ein Nash Gleichgewicht.

Dominante Strategien

Eine Strategie ist dominant, wenn diese Strategie ungeachtet der Reaktion der anderen Spieler immer zu einem größeren Payoff (das kann ein Nutzenniveau, Geld oder etwas anderes sein) als alle anderen Strategien führt. Als Beispiel soll die oben dargestellte Normalform dienen. Zur Vereinfachung soll nur untersucht werden, ob Spieler 1 (der Zeilenspieler) eine dominante Strategie hat. Daher wird nur der Payoff von Spieler 1 angegeben. Außerdem ist es irrelevant wie die Strategien des Spieler 2 lauten, deshalb lautet die erste Spalte einfach nur noch A und die zweite Spalte nur noch B.


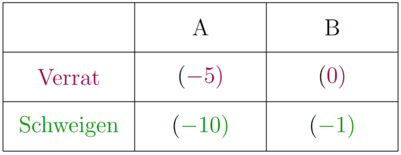
Ist eine der beiden Strategien für Spieler 1 dominant, so ist diese Strategie immer besser. Sollte sich der Spieler 2 für die erste zweite Spalte entscheiden, bringt eine dominante Strategie genauso den größten Payoff der Spalte, wie wenn sich der Spieler zwei für die zweite Spalte entscheidet. In dem oben dargestellten Beispiel ist der Payoff in Spalte A größer, wenn sich Spieler 1 für Verrat entscheidet (-5>-10). Auch in Spalte B ist der Payoff von Verrat größer als der von Schweigen (0>-5). Egal wie sich der Spieler 2 entscheidet, Spieler 1 sollte immer Verrat spielen. Verrat ist eine dominante Strategie und Schweigen eine dominierte Strategie. Damit knüpft der Dominanzbegriff sehr stark an des Konzept der Besten Antwort an.
Es wird zwischen strikter Dominanz und schwacher Dominanz unterschieden. Das oben dargestellte Beispiel stellt strikte Dominanz dar, denn jeder Payoff des Verrats ist strikt größer als der des Schweigens. Schwache Dominanz würde vorliegen, wenn die Payoffs größer oder gleich groß sind, solange mindestens ein Payoff strikt größer ist.
Haben zwei Spieler eine dominante Strategie, spielen sie diese auch in einem der vorhandenen Nash Gleichgewichte. Nicht jede Strategie, die im Nash Gleichgewicht gespielt wird, ist jedoch auch eine dominante Strategie.

IESDS

Das IESDS (Iterated elimination of strictly dominated strategies) ist ein Verfahren, mit dessen Hilfe für Spieler irrationale Strategien eliminiert werden. Ist eine Strategie strikt dominiert, wäre es irrational für einen Spieler diese zu spielen, da mindestens eine Strategie immer einen größeren Payoff liefert. Eine strikt dominante Strategie kann somit als Strategie gestrichen werden.


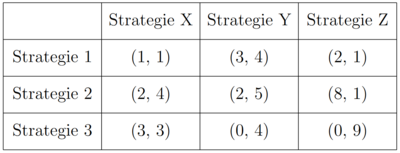
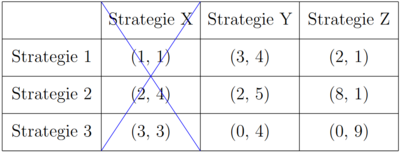
Für Spieler 2 wird die Strategie X von der Strategie Y strikt dominiert (1<4; 4<5; 3<4). Unter der Annahme, dass alle Spieler rational sind, weiß auch Spieler 1, dass Spieler 2 niemals Strategie X wählen wird. Daher muss er die Payoffs in der Strategie X Spalte nicht mehr betrachten. Wenn er dies tut, wird seine Strategie 3 von Strategie 2 strikt dominiert (0<2; 0<8). Dass Strategie 3 auch von Strategie 1 strikt dominiert wird, sei an dieser Stelle auch erwähnt. Es ergibt sich eine neue Spielmatrix, da Spieler 1 niemals Strategie 3 wählen wird.

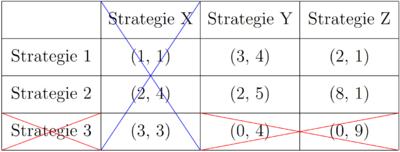
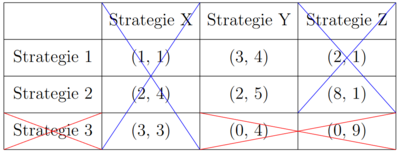
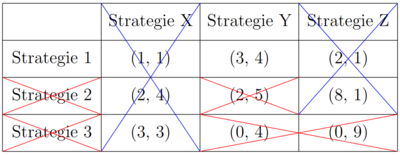
Mit derselben Intuition können die restlichen strikt dominierten Strategien eliminiert werden und der einzig rationale Ausgang ist (Strategie 1, Strategie Y). Bleibt nur eine Strategiekombination übrig, bildet sie immer ein Nash Gleichgewicht. Es können jedoch nicht immer mit der Hilfe des IEDS alle Nash Gleichgewichte gefunden werden.

Teilspielperfektes Nash-Gleichgewicht

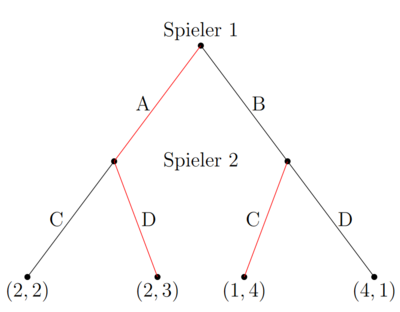
Ein Gleichgewicht ist teilspielperfekt, wenn es ein Nash Gleichgewicht in jedem Teilspiel ist. Hierbei wird das Konzept der Rückwärtsinduktion angewandt. Bei der Rückwärtsinduktion wird das sequenzielle Spiel rückwärts durchlaufen und untersucht, in welchem Entscheidungspunkt (Teilspiel) welcher Spieler wie handeln wird. Das wird für alle Entscheidungspunkte analysiert unabhängig, ob diese im Gleichgewicht erreicht werden oder nicht.

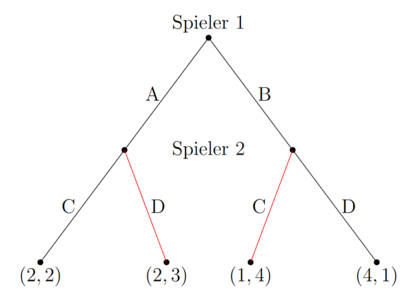
In dem letzten Knotenpunkt, in dem ein Spieler sich entscheiden muss, entscheidet sich Spieler 2 zwischen C oder D. Der zweitgenannte Payoff ist der von Spieler 2. Im linken Knoten erhält er bei C 2 und bei D 3. Da 3>2 wählt er im ersten Fall D. Im rechten Knoten erhält er 4 bei C und 1 bei D. Hier wählt er C. Seine Strategie lautet: "Spiele D, wenn der linke Fall eintritt (Spieler 1 wählt A) und wähle C, wenn der zweite Fall eintritt (Spieler 1 wählt B)".
Spieler 1 weiß, dass das Resultat (A, D) lauten wird, sollte er sich für A entscheiden und (B, C), sollte er sich für B entscheiden. Bei (A, D) erhält er 2 und bei (B, C) erhält er 1. Daher entscheidet sich der rationale Spieler 1 für (A, D).
Das Teilspielperfekte Nash Gleichgewicht lautet:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle TSP\,Nash\,GG=(A, DC) }

Nash Gleichgewicht und Pareto Effizienz

Nash Gleichgewichte sind nicht immer pareto effizient. Paretoeffizienz besteht, wenn keine Partei bessergestellt werden kann, ohne die andere schlechter zu stellen. Pareto effiziente Strategiekombinationen lassen sich sehr gut in der Normalform erkennen. Dafür soll wieder das Gefangenendillema vom Anfang dienen


(Schweigen, Verrat) bringt einen Payoff von (-10, 0). Spieler 1 kann sehr leicht bessergestellt werden. Spielt er zum Beispiel auch Verrat, hat er nicht mehr -10, sondern -5. Die Strategiekombination wäre (Verrat, Verrat). Dadurch wird jedoch Spieler 2 schlechter gestellt. Statt 0 hat er nun -5. (Schweigen, Verrat) ist somit eine Strategiekombination, von der aus keine Partei bessergestellt werden kann, ohne eine andere schlechter zu stellen. Es handelt sich um einen pareto effizienten Ausgang. Lediglich (Verrat, Verrat) ist nicht pareto effizient, da in (Schweigen, Schweigen) beide Spieler besser gestellt werden können.
Es ist deutlich geworden, dass der Begriff des Nash Gleichgewichts und der des Pareto Effizienz ganz andere Thematiken abdecken.

MC Aufgaben

Welche der folgenden Aussagen ist falsch?

	Nicht jedes teilspielperfekte Nash-Gleichgewicht eines Spiels in extensiver Form ist auch ein Nash-Gleichgewicht des Spiels in Normalform.
	Nicht jedes Gleichgewicht in dominanten Strategien des Spiels in Normalform ist auch ein teilspielperfektes Nash-Gleichgewicht des Spiels in extensiver Form.
	Nicht jedes Nash-Gleichgewicht des Spiels in Normalform ist auch ein teilspielperfektes Nash-Gleichgewicht des Spiels in extensiver Form.

Die folgenden Aussagen beziehen sich auf statische Spiele. Welche Aussage ist wahr?

	Es gibt gemischte Nash Gleichgewichte, in denen ein Spieler eine strikt dominierte Strategie spielt.
	Jedes Nash Gleichgewicht in reinen Strategien überlebt das IESDS Verfahren.
	Jedes Strategieprofil, das das IESDS Verfahren überlebt, ist ein Nash Gleichgewicht.

Welche der folgenden Aussagen ist richtig?

	Beim IESDS hängt das Ergebnis von der Reihenfolge der Eliminierung ab.
	Beim IESDS hängt das Ergebnis nicht von der Reihenfolge der Eliminierung ab.
	Das IESDS eliminiert gegebenenfalls Nash Gleichgewichte in gemischten Strategien.
	Das IESDS eliminiert gegebenenfalls Nash Gleichgewichte in reinen Strategien.