Edgeworth-Box: Unterschied zwischen den Versionen
Lobin (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
__TOC__ | __TOC__ | ||
| − | ==Die Box== | + | ==Die (Edgeworth-)Box== |
| − | Die Box der Edgeworth-Box ist die grafische Darstellung, wie zwei begrenzte Güter zwischen zwei Haushalten aufgeteilt werden können. | + | Die Box der Edgeworth-Box ist die grafische Darstellung, wie zwei begrenzte Güter zwischen zwei Haushalten aufgeteilt werden können. In diesem Modell besitzen beide Haushalte eine bestimmte Anfangsausstattung der beiden Güter und diese können sie miteinander tauschen. Die konsumierte Menge des Haushaltes A ist hierbei abhängig von der konsumierten Menge von Haushalt B desselben Gutes. Angenommen von einem Gut <math> x_1 </math> existieren 10 Einheiten. Wenn Haushalt B von den 10 Haushalten 7 konsumiert, konsumiert Haushalt A 3 Einheiten. <br> |
<math> x_1^{A}=x_1^{max}-x_1^{B}=10-7 </math> <br> | <math> x_1^{A}=x_1^{max}-x_1^{B}=10-7 </math> <br> | ||
Beziehungsweise <math> x_1^{max}=x_1^{A}+x_1^{B} </math> <br> | Beziehungsweise <math> x_1^{max}=x_1^{A}+x_1^{B} </math> <br> | ||
| − | Dasselbe gilt für das andere Gut <math> x_2 </math>. Die beschriebenen Relationen der Konsummenge kann in einem Viereck | + | Dasselbe gilt für das andere Gut <math> x_2 </math>. Die beschriebenen Relationen der Konsummenge kann in einem Viereck darstellt werden. Das Viereck/ die Box verdeutlicht jede mögliche Kombination, wie die zwei Güter zwischen den beiden Konsumenten aufgeteilt werden kann. Jeder Punkt innerhalb der Box ist theoretisch mit den Anfangsausstattungen und einem Tausch möglich. Alles was außerhalb der Box liegt ist wiederum nicht möglich, da die Güter in dem Modell begrenzt sind. Wenn beide Konsumenten zusammen nur 10 Einheiten eines Gutes besitzen, können insgesamt auch nur 10 konsumiert werden. <br> |
[[Datei:Edgeworthbox6.png|400px|rahmenlos]] <br clear=all> | [[Datei:Edgeworthbox6.png|400px|rahmenlos]] <br clear=all> | ||
Die horizontale Gerade beschreibt die Menge von <math> x_1 </math>. Je weiter rechts der Konsumpunkt liegt, desto mehr konsumiert A von diesem Gut und desto weniger B. Die vertikale Gerade beschreibt die Aufteilung des Gutes <math> x_2 </math>. Je weiter oben der Konsumpunkt liegt, desto mehr konsumiert A von <math> x_2 </math> und desto weniger B. | Die horizontale Gerade beschreibt die Menge von <math> x_1 </math>. Je weiter rechts der Konsumpunkt liegt, desto mehr konsumiert A von diesem Gut und desto weniger B. Die vertikale Gerade beschreibt die Aufteilung des Gutes <math> x_2 </math>. Je weiter oben der Konsumpunkt liegt, desto mehr konsumiert A von <math> x_2 </math> und desto weniger B. | ||
| Zeile 22: | Zeile 22: | ||
==Effiziente Allokation mit Anfangsausstattung== | ==Effiziente Allokation mit Anfangsausstattung== | ||
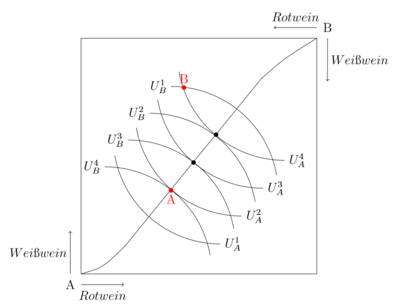
| − | Die Edgeworthbox zeigt, dass es nutzenmaximierend und damit [[effizient]] ist, in einer geschlossenen Volkswirtschaft zu handeln, beziehungsweise zu tauschen. Um zu verstehen warum das so ist soll ein Szenario dienen, in dem beide Haushalte von Grund aus eine Anfangsausstattug haben, wie sie in dem Punkt A dargestellt ist. Haushalt A's Anfangsausstattung würde zu einem Nutzenniveau von <math> U_A{3} </math> führen und Haushalbt B zu einem Niveau von <math> U_B^{2} </math>. Es gibt viele Möglichkeiten, um die Effizienz zu steigern. Für den Anfang soll das Nutzenniveau von Haushalt A konstant gehalten werden. Sollte es zu einem Handel kommen, möchte der Haushalt A nach dem Handel nicht schlechter gestellt sein, als vor dem Handel. Solange sein altes Nutzenniveau erreicht wird, stimmt es jedem Tauschgeschäft zu. Bei einem Handel, der zum Punkt B führt, gibt Haushalt A von <math> x_1 </math> ab und erhält dafür mehr von <math> x_2 </math>. Haushalt A befindet sich durch den Handel weiterhin auf <math> U_A{3} </math>. Der Haushalt B befindet sich nun jedoch auf <math> U_B{3} </math> und damit auf einem höheren Nutzenniveau. Durch den Handel ist es gelungen eine Partei besser zu stellen, ohne die andere schlechter zu stellen. Ausgehend von dem Ausstattungspunkt A existieren jedoch viele [[pareto | + | Die Edgeworthbox zeigt, dass es nutzenmaximierend und damit [[Effizienz|effizient]] ist, in einer geschlossenen Volkswirtschaft zu handeln, beziehungsweise zu tauschen. Um zu verstehen warum das so ist soll ein Szenario dienen, in dem beide Haushalte von Grund aus eine Anfangsausstattug haben, wie sie in dem Punkt A dargestellt ist. Haushalt A's Anfangsausstattung würde zu einem Nutzenniveau von <math> U_A^{3} </math> führen und Haushalbt B zu einem Niveau von <math> U_B^{2} </math>. Es gibt viele Möglichkeiten, um die Effizienz zu steigern. Für den Anfang soll das Nutzenniveau von Haushalt A konstant gehalten werden. Sollte es zu einem Handel kommen, möchte der Haushalt A nach dem Handel nicht schlechter gestellt sein, als vor dem Handel. Solange sein altes Nutzenniveau erreicht wird, stimmt es jedem Tauschgeschäft zu. Bei einem Handel, der zum Punkt B führt, gibt Haushalt A von <math> x_1 </math> ab und erhält dafür mehr von <math> x_2 </math>. Haushalt A befindet sich durch den Handel weiterhin auf <math> U_A^{3} </math>. Der Haushalt B befindet sich nun jedoch auf <math> U_B^{3} </math> und damit auf einem höheren Nutzenniveau. Durch den Handel ist es gelungen eine Partei besser zu stellen, ohne die andere schlechter zu stellen. Ausgehend von dem Ausstattungspunkt A existieren jedoch viele [[Effizienz#Pareto-Effizienz|pareto effizient]] Konsumpunkte, die durch einen Tausch erreicht werden können. Diese liegen alle zwischen <math> U_A^{3} </math> und <math> U_B^2 </math>. <br> |
Die effiziente Allokation innerhalb der Edgeworthbox zeigt, dass der [[Effizienz#Hauptsatz der Wohlfahrtsökonomik|Hauptsatz der Wohlfahrtsökonomik]] gilt. <br> | Die effiziente Allokation innerhalb der Edgeworthbox zeigt, dass der [[Effizienz#Hauptsatz der Wohlfahrtsökonomik|Hauptsatz der Wohlfahrtsökonomik]] gilt. <br> | ||
[[Datei:Edgeworthbox7.png|400px|rahmenlos]] | [[Datei:Edgeworthbox7.png|400px|rahmenlos]] | ||
==Kontraktkurve== | ==Kontraktkurve== | ||
| − | Die Kontraktkurve ist die Verbindungslinie aller Tangentialpunkte der [[Präferenzen und Indifferenzkurven#Indifferenzkurven|Indifferenzkurven]]. Alle Punkte, die auf der Kontraktkurve liegen sind [[pareto effizient]]. Gegeben unterschiedlicher Anfangsausstattungen werden Tauschgeschäfte im Modell immer in einen Punkt auf der Kontraktkurve resultieren. <br> | + | Die Kontraktkurve ist die Verbindungslinie aller Tangentialpunkte der [[Präferenzen und Indifferenzkurven#Indifferenzkurven|Indifferenzkurven]]. Alle Punkte, die auf der Kontraktkurve liegen sind [[Effizienz#Pareto-Effizienz|pareto effizient]]. Gegeben unterschiedlicher Anfangsausstattungen werden Tauschgeschäfte im Modell immer in einen Punkt auf der Kontraktkurve resultieren. <br> |
[[Datei:Edgeworthbox4.png|400px|rahmenlos]] | [[Datei:Edgeworthbox4.png|400px|rahmenlos]] | ||
==Marktgleichgewicht== | ==Marktgleichgewicht== | ||
| − | Bisher ergab sich eine unendliche Menge von | + | [[Datei:Edgeworthbox8.png|400px|rahmenlos]] <br clear=all> |
| − | Der Punkt E lässt sich auch rechnerisch ermitteln. Hierfür dient das [[Lagrangeverfahren]]. Ziel ist den Nutzen zu maximieren unter der Nebenbedingung, dass der Haushalt durch den Ausstattungspunkt im Budget limitiert ist. <br> | + | Bisher ergab sich eine unendliche Menge von Gleichgewichtszuständen entlang der Kontraktkurve. Nun stellt sich die Frage, welcher davon tatsächlich realisiert wird. Wird von einem speziellen Tauschprozess, dem Konkurrenzmarktgleichgewicht ausgegangen, entspricht dies genau einem ganz bestimmten Gleichgewicht und somit einem einzigen Punkt auf der Kontraktkurve in der Edgeworth-Box. Grafisch ist das Marktgleichgewicht ausgehend von dem Ausstattungspunkt E im Punkt D erkennbar. In diesem Punkt tangiert die Indifferenzkurve des Haushalts A die Indifferenzkurve des Haushalts B. Außerdem tangieren die beiden Indifferenzkurven eine Gerade, die durch das Preisverhältnis gekennzeichnet ist. <br> |
| − | '''Die Budgetrestriktion''': Die [[Budgetrestriktion und Budgetgerade#Budgetrestriktion|Budgetrestriktion]] gestaltet sich in den Ausgaben, wie bereits bekannt. Die Preise werden mit den Mengen multipliziert. Das Budget gestaltet sich anders. Faktisch hat der Haushalt keinen Geldbetrag zur Verfügung, den er ausgeben kann. Stattdessen hat er | + | Der Punkt E lässt sich auch rechnerisch ermitteln. Hierfür dient das [[Lagrange|Lagrangeverfahren]]. Ziel ist den Nutzen zu maximieren unter der Nebenbedingung, dass der Haushalt durch den Ausstattungspunkt im Budget limitiert ist. <br> |
| + | '''Die Budgetrestriktion''': Die [[Budgetrestriktion und Budgetgerade#Budgetrestriktion|Budgetrestriktion]] gestaltet sich in den Ausgaben, wie bereits bekannt. Die Preise werden mit den Mengen multipliziert. Das Budget gestaltet sich anders. Faktisch hat der Haushalt keinen Geldbetrag zur Verfügung, den er ausgeben kann. Stattdessen hat er seine Anfangsausstattung, das er eintauschen kann. Dies kann er zu den Preisen <math> p_1 </math> und <math> p_2 </math>. <br> | ||
<math> p_1x_1+p_2x_2 \leq p_1 \tilde{x_1}^{A}+p_2 \tilde{x_2}^{A} </math> <br> | <math> p_1x_1+p_2x_2 \leq p_1 \tilde{x_1}^{A}+p_2 \tilde{x_2}^{A} </math> <br> | ||
Die Langrange Funktion lautet nun <br> | Die Langrange Funktion lautet nun <br> | ||
| Zeile 61: | Zeile 62: | ||
|type="()"} | |type="()"} | ||
+ ...würde von Person B befürwortet werden und von Person A nicht. | + ...würde von Person B befürwortet werden und von Person A nicht. | ||
| − | - ...wäre pareto | + | - ...wäre eine pareto Verbesserung, da die Allokation auf der Kontraktkurve liegt. |
- ...würde von Person A befürwortet werden und von Person B nicht. | - ...würde von Person A befürwortet werden und von Person B nicht. | ||
- ...würde von beiden Personen abgelehnt werden, da beide etwas aufgeben müssten. | - ...würde von beiden Personen abgelehnt werden, da beide etwas aufgeben müssten. | ||
Aktuelle Version vom 12. Februar 2024, 23:27 Uhr
Definition
Die Edgeworth-Box ist die grafische Darstellung einer geschlossenen Tauschökonomie mit den Präferenzen zweier Haushalte und zwei unterschiedlichen Gütern. Die Güter sind in ihrer Anzahl begrenzt.
Die (Edgeworth-)Box
Die Box der Edgeworth-Box ist die grafische Darstellung, wie zwei begrenzte Güter zwischen zwei Haushalten aufgeteilt werden können. In diesem Modell besitzen beide Haushalte eine bestimmte Anfangsausstattung der beiden Güter und diese können sie miteinander tauschen. Die konsumierte Menge des Haushaltes A ist hierbei abhängig von der konsumierten Menge von Haushalt B desselben Gutes. Angenommen von einem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
existieren 10 Einheiten. Wenn Haushalt B von den 10 Haushalten 7 konsumiert, konsumiert Haushalt A 3 Einheiten.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1^{A}=x_1^{max}-x_1^{B}=10-7 }
Beziehungsweise Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1^{max}=x_1^{A}+x_1^{B} }
Dasselbe gilt für das andere Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
. Die beschriebenen Relationen der Konsummenge kann in einem Viereck darstellt werden. Das Viereck/ die Box verdeutlicht jede mögliche Kombination, wie die zwei Güter zwischen den beiden Konsumenten aufgeteilt werden kann. Jeder Punkt innerhalb der Box ist theoretisch mit den Anfangsausstattungen und einem Tausch möglich. Alles was außerhalb der Box liegt ist wiederum nicht möglich, da die Güter in dem Modell begrenzt sind. Wenn beide Konsumenten zusammen nur 10 Einheiten eines Gutes besitzen, können insgesamt auch nur 10 konsumiert werden.
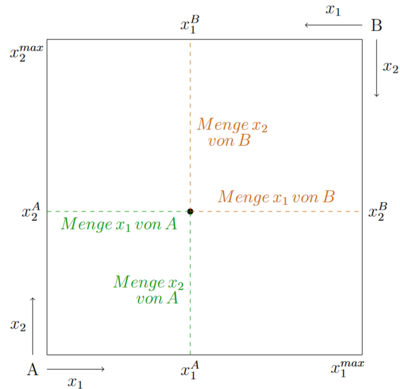
Die horizontale Gerade beschreibt die Menge von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
. Je weiter rechts der Konsumpunkt liegt, desto mehr konsumiert A von diesem Gut und desto weniger B. Die vertikale Gerade beschreibt die Aufteilung des Gutes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
. Je weiter oben der Konsumpunkt liegt, desto mehr konsumiert A von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
und desto weniger B.
Präferenzen in der Edgeworth-Box
Haushalte weisen in ihrem Konsumverhalten Präferenzen auf. Die grafische Darstellung der Präferenzen erfolgt über Indifferenzkurven entlang derer das Nutzenniveau konstant ist.
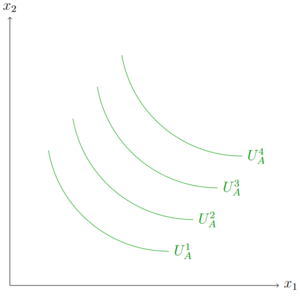
Im Weiteren sollen nicht nur die Präferenzen eines Haushalts, sondern auch die Präferenzen eines zweiten Haushalts betrachtet werden. Um die Präferenzen in der Edgeworthbox darzustellen, wird das Koordinatensystems eines Haushalts um 180 Grad gedreht.
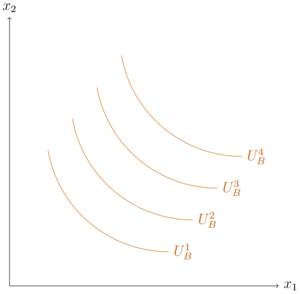
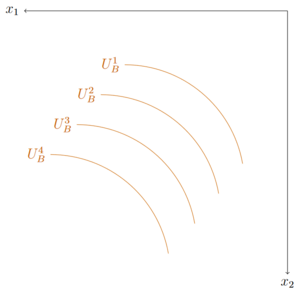
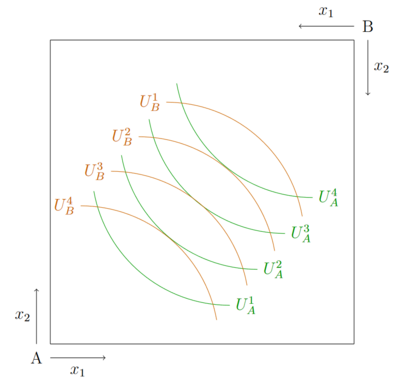
Werden die Koordinatensysteme des Haushalts A und des Haushalts B mit den jeweiligen Präferenzen übereinandergelegt, entsteht die Edgeworth-Box. Anhand dieser wird deutlich, in welchen Punkten es effizient ist zu konsumieren. In der Edgeworth-Box gibt es unendlich viele Indifferenzkurven, von denen einige unten eingezeichnet sind. Einige Indifferenzkurven des Haushalts A tangieren jeweils eine Indifferenzkurve des Haushalts B. Diese tangential Punkte beschreiben effiziente Allokationen.
Effiziente Allokation mit Anfangsausstattung
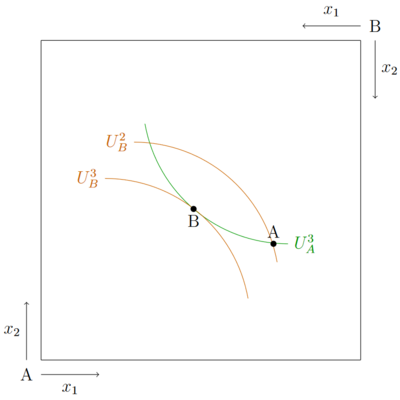
Die Edgeworthbox zeigt, dass es nutzenmaximierend und damit effizient ist, in einer geschlossenen Volkswirtschaft zu handeln, beziehungsweise zu tauschen. Um zu verstehen warum das so ist soll ein Szenario dienen, in dem beide Haushalte von Grund aus eine Anfangsausstattug haben, wie sie in dem Punkt A dargestellt ist. Haushalt A's Anfangsausstattung würde zu einem Nutzenniveau von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_A^{3} }
führen und Haushalbt B zu einem Niveau von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_B^{2} }
. Es gibt viele Möglichkeiten, um die Effizienz zu steigern. Für den Anfang soll das Nutzenniveau von Haushalt A konstant gehalten werden. Sollte es zu einem Handel kommen, möchte der Haushalt A nach dem Handel nicht schlechter gestellt sein, als vor dem Handel. Solange sein altes Nutzenniveau erreicht wird, stimmt es jedem Tauschgeschäft zu. Bei einem Handel, der zum Punkt B führt, gibt Haushalt A von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
ab und erhält dafür mehr von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
. Haushalt A befindet sich durch den Handel weiterhin auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_A^{3} }
. Der Haushalt B befindet sich nun jedoch auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_B^{3} }
und damit auf einem höheren Nutzenniveau. Durch den Handel ist es gelungen eine Partei besser zu stellen, ohne die andere schlechter zu stellen. Ausgehend von dem Ausstattungspunkt A existieren jedoch viele pareto effizient Konsumpunkte, die durch einen Tausch erreicht werden können. Diese liegen alle zwischen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_A^{3} }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_B^2 }
.
Die effiziente Allokation innerhalb der Edgeworthbox zeigt, dass der Hauptsatz der Wohlfahrtsökonomik gilt.
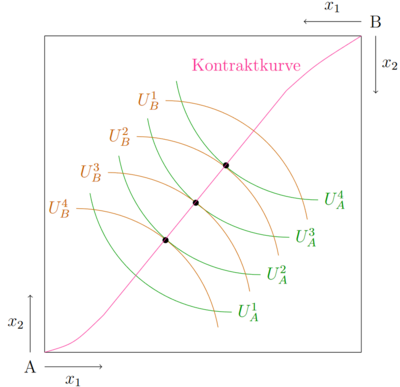
Kontraktkurve
Die Kontraktkurve ist die Verbindungslinie aller Tangentialpunkte der Indifferenzkurven. Alle Punkte, die auf der Kontraktkurve liegen sind pareto effizient. Gegeben unterschiedlicher Anfangsausstattungen werden Tauschgeschäfte im Modell immer in einen Punkt auf der Kontraktkurve resultieren.
Marktgleichgewicht
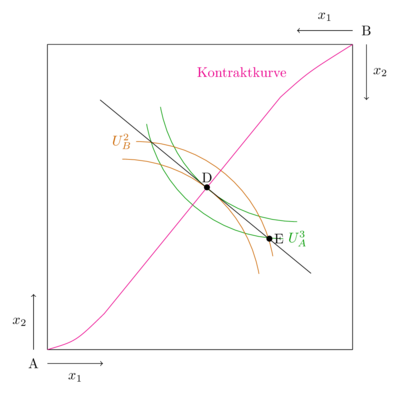
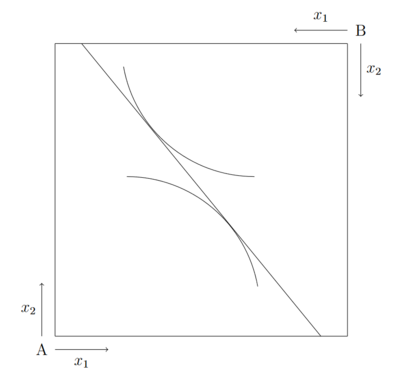
Bisher ergab sich eine unendliche Menge von Gleichgewichtszuständen entlang der Kontraktkurve. Nun stellt sich die Frage, welcher davon tatsächlich realisiert wird. Wird von einem speziellen Tauschprozess, dem Konkurrenzmarktgleichgewicht ausgegangen, entspricht dies genau einem ganz bestimmten Gleichgewicht und somit einem einzigen Punkt auf der Kontraktkurve in der Edgeworth-Box. Grafisch ist das Marktgleichgewicht ausgehend von dem Ausstattungspunkt E im Punkt D erkennbar. In diesem Punkt tangiert die Indifferenzkurve des Haushalts A die Indifferenzkurve des Haushalts B. Außerdem tangieren die beiden Indifferenzkurven eine Gerade, die durch das Preisverhältnis gekennzeichnet ist.
Der Punkt E lässt sich auch rechnerisch ermitteln. Hierfür dient das Lagrangeverfahren. Ziel ist den Nutzen zu maximieren unter der Nebenbedingung, dass der Haushalt durch den Ausstattungspunkt im Budget limitiert ist.
Die Budgetrestriktion: Die Budgetrestriktion gestaltet sich in den Ausgaben, wie bereits bekannt. Die Preise werden mit den Mengen multipliziert. Das Budget gestaltet sich anders. Faktisch hat der Haushalt keinen Geldbetrag zur Verfügung, den er ausgeben kann. Stattdessen hat er seine Anfangsausstattung, das er eintauschen kann. Dies kann er zu den Preisen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1 }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_2 }
.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1x_1+p_2x_2 \leq p_1 \tilde{x_1}^{A}+p_2 \tilde{x_2}^{A} }
Die Langrange Funktion lautet nun
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{L}_A(x_1,x_2,\lambda)=U_A(x_1,x_2)+\lambda(p_1 \tilde{x_1}^{A}+p_2-p_1x_1-p_2x_2) }
Das Maximieren ergibt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\frac{\part U_A}{\part x_1}}{\frac{\part U_A}{\part x_2}}=GRS^{A}=\frac{p_1}{p_2} }
Das gleiche für Haushalt B ergibt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\frac{\part U_B}{\part x_1}}{\frac{\part U_B}{\part x_2}}=GRS^{B}=\frac{p_1}{p_2} }
Es muss also gelten
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GRS^{A}=\frac{p_1}{p_2}=GRS^{B} }
MC Fragen
Die ersten beiden Fragen beziehen sich auf folgende Edgeworthbox: