Risiko und Risikoeinstellung: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
|||
| (5 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
==Risiko== | ==Risiko== | ||
Eine Lotterie stellt eine Situation mit Risiko dar. Ein Beispiel einer Lotterie ist der Münzwurf mit Wetteinsatz. Die Wahrscheinlichkeiten für Kopf und Zahl sind mit jeweils 0.5 bekannt. Fällt die zuvor gewählte Seite wird der Einsatz gewonnen, fällt er auf die andere Seite ist der Einsatz verloren. <br> | Eine Lotterie stellt eine Situation mit Risiko dar. Ein Beispiel einer Lotterie ist der Münzwurf mit Wetteinsatz. Die Wahrscheinlichkeiten für Kopf und Zahl sind mit jeweils 0.5 bekannt. Fällt die zuvor gewählte Seite wird der Einsatz gewonnen, fällt er auf die andere Seite ist der Einsatz verloren. <br> | ||
| − | ''Beispiel:'' Daniel und Oskar wetten auf das Ergebnis eines Münzwurfs. Daniel tippt auf Kopf und Oskar auf Zahl. Derjenige dessen Seite oben liegt erhält von dem anderen den Wetteinsatz von 10€. Allgemein kann eine solche Lotterie X in folgender Form dargestellt werden: <math> X=(x_{1}, p_{1};x_{2}, p_{2};...x_{n}, p_{n}) </math>, wobei <math> n = 1,2,3.. </math> und <math> p_{i} > 0 </math> . <math> x_{i} </math> stellt die Auszahlung dar, die mit einer Wahrscheinlichkeit <math> p_{i} </math> eintritt. In dem Fall des Münzwurfs würde dies folgende Lotterie bedeuten X=(0, 0.5; 10, 0.5). | + | ''Beispiel:'' Daniel und Oskar wetten auf das Ergebnis eines Münzwurfs. Daniel tippt auf Kopf und Oskar auf Zahl. Derjenige dessen Seite oben liegt erhält von dem anderen den Wetteinsatz von 10€. Allgemein kann eine solche Lotterie X in folgender Form dargestellt werden: <math> X=(x_{1}, p_{1};x_{2}, p_{2};...x_{n}, p_{n}) </math>, wobei <math> n = 1,2,3,... </math> und <math> p_{i} > 0 </math> . <math> x_{i} </math> stellt die Auszahlung dar, die mit einer Wahrscheinlichkeit <math> p_{i} </math> eintritt. In dem Fall des Münzwurfs würde dies folgende Lotterie bedeuten X=(0, 0.5; 10, 0.5). |
==Entscheidung unter Unsicherheit== | ==Entscheidung unter Unsicherheit== | ||
| Zeile 22: | Zeile 22: | ||
<big> <math display="inline"> \frac{\part^{2} U(x)}{\part^{2} x} </math> > 0 </big> <br> | <big> <math display="inline"> \frac{\part^{2} U(x)}{\part^{2} x} </math> > 0 </big> <br> | ||
<br> | <br> | ||
| − | [[Datei:Risikofreude.png| | + | [[Datei:Risikofreude.png|400px|rahmenlos]] <br> |
<br clear=all> | <br clear=all> | ||
In dem grafischen Beispiel wird eine Lotterie X, X=(0.5, 10; 0.5, 30), betrachtet. Der Erwartungswert der Lotterie lautet 20 und der Nutzen des Erwartungswert liegt auf der grünen [[Präferenzen und Indifferenzkurven#Präferenzen und Nutzenfunktion|Nutzenfunktion]]. Mit einer Wahrscheinlichkeit von 0.5 erfährt das Individuum einen Nutzen von 10, U(10), und mit einer Wahrscheinlichkeit von 0.5 einen Nutzen von 30, U(30). Der erwartete Nutzen der Lotterie liegt auf der gestrichelten Verbindungslinie von U(10) zu U(30) und ist größer als der Nutzen des Erwartungswertes. Ist die Wahrscheinlichkeitsverteilung der beiden Auszahlungen verändert, so liegt der Erwartungsnutzen weiterhin auf der gestrichelten Verbindungslinie und ist in die Richtung der größeren Wahrscheinlichkeit verschoben. Die Risikoeinstellung des Individuums ist davon nicht betroffen. | In dem grafischen Beispiel wird eine Lotterie X, X=(0.5, 10; 0.5, 30), betrachtet. Der Erwartungswert der Lotterie lautet 20 und der Nutzen des Erwartungswert liegt auf der grünen [[Präferenzen und Indifferenzkurven#Präferenzen und Nutzenfunktion|Nutzenfunktion]]. Mit einer Wahrscheinlichkeit von 0.5 erfährt das Individuum einen Nutzen von 10, U(10), und mit einer Wahrscheinlichkeit von 0.5 einen Nutzen von 30, U(30). Der erwartete Nutzen der Lotterie liegt auf der gestrichelten Verbindungslinie von U(10) zu U(30) und ist größer als der Nutzen des Erwartungswertes. Ist die Wahrscheinlichkeitsverteilung der beiden Auszahlungen verändert, so liegt der Erwartungsnutzen weiterhin auf der gestrichelten Verbindungslinie und ist in die Richtung der größeren Wahrscheinlichkeit verschoben. Die Risikoeinstellung des Individuums ist davon nicht betroffen. | ||
| Zeile 36: | Zeile 36: | ||
<big> <math display="inline"> \frac{\part^{2} U(x)}{\part^{2} x} </math> = 0 </big> <br> | <big> <math display="inline"> \frac{\part^{2} U(x)}{\part^{2} x} </math> = 0 </big> <br> | ||
<br> | <br> | ||
| − | [[Datei:Risikoneutralität.png| | + | [[Datei:Risikoneutralität.png|400px|rahmenlos]] <br> |
<br clear=all> | <br clear=all> | ||
Dieselbe Lotterie X, die bereits bei der [[Risiko und Risikoeinstellung#Risikofreude|Risikofreude]] eine Rolle spielte, sieht mit der Nutzenfunktion einer risikoneutralen Person wie oben ersichtlich aus. Der Erwartungsnutzen ist genauso groß wie der Nutzen des Erwartungswertes (die Nutzenniveaus liegen aufeinander) und für die Person spielt es keine Rolle, ob sie den Erwartungswert der Lotterie ausgezahlt bekommt oder ob sie an der Lotterie teilnimmt. | Dieselbe Lotterie X, die bereits bei der [[Risiko und Risikoeinstellung#Risikofreude|Risikofreude]] eine Rolle spielte, sieht mit der Nutzenfunktion einer risikoneutralen Person wie oben ersichtlich aus. Der Erwartungsnutzen ist genauso groß wie der Nutzen des Erwartungswertes (die Nutzenniveaus liegen aufeinander) und für die Person spielt es keine Rolle, ob sie den Erwartungswert der Lotterie ausgezahlt bekommt oder ob sie an der Lotterie teilnimmt. | ||
| Zeile 46: | Zeile 46: | ||
<big> <math display="inline"> \frac{\part^{2} U(x)}{\part^{2} x} </math> < 0 </big> <br> | <big> <math display="inline"> \frac{\part^{2} U(x)}{\part^{2} x} </math> < 0 </big> <br> | ||
<br> | <br> | ||
| − | [[Datei:Risikoaversion.png| | + | [[Datei:Risikoaversion.png|400px|rahmenlos]] <br> |
<br clear=all> | <br clear=all> | ||
Der Erwartungsnutzen der Lotterie, der je nach Wahrscheinlichkeitsverteilung irgendwo auf der gestrichelten Verbindungslinie der beiden Nutzenniveaus liegt, liegt unter dem Nutzen, den der Erwartungswert der Lotterie bedeutet. Die Gefahr weniger zu erhalten, wiegt schwerer als die Chance mehr zu erhalten. Dies liegt am [[Marginale Sichtweise|abnehmenden Grenznutzen des Einkommens]]. Zusätzliches Einkommen erhöht das Nutzenniveau, dies jedoch weniger als die Einheit vorher. | Der Erwartungsnutzen der Lotterie, der je nach Wahrscheinlichkeitsverteilung irgendwo auf der gestrichelten Verbindungslinie der beiden Nutzenniveaus liegt, liegt unter dem Nutzen, den der Erwartungswert der Lotterie bedeutet. Die Gefahr weniger zu erhalten, wiegt schwerer als die Chance mehr zu erhalten. Dies liegt am [[Marginale Sichtweise|abnehmenden Grenznutzen des Einkommens]]. Zusätzliches Einkommen erhöht das Nutzenniveau, dies jedoch weniger als die Einheit vorher. | ||
| Zeile 53: | Zeile 53: | ||
Das Sicherheitsäquivalent (SÄ) ist das (sichere) Einkommen, dessen Nutzen äquivalent zu dem erwarteten Nutzen der Lotterie ist. Dementsprechend gilt U(SÄ)=E(U). Um das Sicherheitsäquivalent mathematisch herauszufinden, gilt es die Nutzenfunktion mit dem erwarteten Nutzen des unsicheren Einkommens gleichzusetzen und nach der unabhängigen Variable umzustellen. Grafisch kann das Sicherheitsäquivalent wie folgt dargestellt werden: <br> | Das Sicherheitsäquivalent (SÄ) ist das (sichere) Einkommen, dessen Nutzen äquivalent zu dem erwarteten Nutzen der Lotterie ist. Dementsprechend gilt U(SÄ)=E(U). Um das Sicherheitsäquivalent mathematisch herauszufinden, gilt es die Nutzenfunktion mit dem erwarteten Nutzen des unsicheren Einkommens gleichzusetzen und nach der unabhängigen Variable umzustellen. Grafisch kann das Sicherheitsäquivalent wie folgt dargestellt werden: <br> | ||
<br> | <br> | ||
| − | [[Datei:SÄ.png| | + | [[Datei:SÄ.png|400px|rahmenlos]] <br> |
<br clear=all> | <br clear=all> | ||
Aus den unterschiedlichen Nutzenfunktionen ergeben sich folgende Zusammenhänge: <br> | Aus den unterschiedlichen Nutzenfunktionen ergeben sich folgende Zusammenhänge: <br> | ||
| Zeile 65: | Zeile 65: | ||
Die Risikoprämie (RP) ist die maximale Geldsumme, die eine risikoaverse Person zur Vermeidung eines Risikos zu zahlen bereit ist. Die maximale Geldsumme ist die Differenz des Erwartungswert der Auszahlung und dem [[Risiko und Risikoeinstellung#Sicherheitsäquivalenz|Sicherheitsäquivalent]] einer risikoaversen Person. | Die Risikoprämie (RP) ist die maximale Geldsumme, die eine risikoaverse Person zur Vermeidung eines Risikos zu zahlen bereit ist. Die maximale Geldsumme ist die Differenz des Erwartungswert der Auszahlung und dem [[Risiko und Risikoeinstellung#Sicherheitsäquivalenz|Sicherheitsäquivalent]] einer risikoaversen Person. | ||
<br> | <br> | ||
| − | Im ''Beispiel'' von oben ist der Erwartungswert der beiden Gehaltsmöglichkeiten 20. Im Beispiel ist der Bewerber eine risikoaverse Person, weshalb die Differenz E[X] - SÄ größer null und daher positiv ist. Das Sicherheitsäquivalent ist das sichere Gehalt, das einen identisch großen Nutzen wie das unsichere Gehaltsmodell liefert (das sichere Äquivalent zur unsicheren Option). Der Bewerber ist bereit die Differenz zu zahlen, um der Unsicherheit zu entgehen und bleibt gleichzeitig auf demselben Nutzenniveau. | + | Im ''Beispiel'' von oben ist der Erwartungswert der beiden Gehaltsmöglichkeiten 20. Im Beispiel ist der Bewerber eine risikoaverse Person, weshalb die Differenz E[X] - SÄ größer null und daher positiv ist. Das Sicherheitsäquivalent ist das sichere Gehalt, das einen identisch großen Nutzen wie das unsichere Gehaltsmodell liefert (das sichere Äquivalent zur unsicheren Option). Der Bewerber ist bereit die Differenz zu zahlen, um der Unsicherheit zu entgehen und bleibt gleichzeitig auf demselben Nutzenniveau. Die Risikoprämie ist in der Abbildung unten als Differenz in rot eingezeichnet. <br> |
| + | [[Datei:RP.png|400px|rahmenlos]] | ||
==Versicherungsprämie== | ==Versicherungsprämie== | ||
| Zeile 97: | Zeile 98: | ||
<quiz display=simple shuffleanswers=true> | <quiz display=simple shuffleanswers=true> | ||
| − | {Welche Risikopräferenzen hat eine Person mit folgender Nutzenfunktion für X Werte größer 1? <math> \frac{x^{2}}{e^{x}} </math> | + | {Welche Risikopräferenzen hat eine Person mit folgender Nutzenfunktion für X Werte größer 1? <math> U(x)=\frac{x^{2}}{e^{x}} </math> |
|type="()"} | |type="()"} | ||
| − | + | - Die Person ist risikoavers. | |
- Die Person ist risikoneutral. | - Die Person ist risikoneutral. | ||
- Die Person ist risikofreudig. | - Die Person ist risikofreudig. | ||
| − | + | + Die Risikopräferenzen variieren in x, wobei x > 1. | |
</quiz> | </quiz> | ||
Aktuelle Version vom 22. Februar 2024, 15:05 Uhr
Definition
Risiko bezieht sich auf Situationen, in denen unterschiedlich mögliche Ergebnisse eintreten können. Im Standardfall sind hierbei die Wahrscheinlichkeit des Eintretens aller Ergebnisse bekannt. Demnach wird im Folgenden zwischen der subjektiven und der objektiven Wahrscheinlichkeit differenziert und die objektive Wahrscheinlichkeit als Kennziffer herangezogen.
Risiko
Eine Lotterie stellt eine Situation mit Risiko dar. Ein Beispiel einer Lotterie ist der Münzwurf mit Wetteinsatz. Die Wahrscheinlichkeiten für Kopf und Zahl sind mit jeweils 0.5 bekannt. Fällt die zuvor gewählte Seite wird der Einsatz gewonnen, fällt er auf die andere Seite ist der Einsatz verloren.
Beispiel: Daniel und Oskar wetten auf das Ergebnis eines Münzwurfs. Daniel tippt auf Kopf und Oskar auf Zahl. Derjenige dessen Seite oben liegt erhält von dem anderen den Wetteinsatz von 10€. Allgemein kann eine solche Lotterie X in folgender Form dargestellt werden: , wobei und . stellt die Auszahlung dar, die mit einer Wahrscheinlichkeit eintritt. In dem Fall des Münzwurfs würde dies folgende Lotterie bedeuten X=(0, 0.5; 10, 0.5).
Entscheidung unter Unsicherheit
Situtationen, in denen Risiko existiert und in denen Individuen entscheidungen treffen müssen, sind geprägt von Unsicherheit. Um Entscheidungen unter Unsicherheit genauer zu verstehen, wird auf das Beispiel einer Anlageoption, die mit bekannten Wahrscheinlichkeiten unterschiedliche Werte auszahlt, zurück gegriffen. Nehmen wir an, der Entscheidungsträger hat die Alternative nichts zu tun (was eine Auszahlung von Null nach sich zieht) oder in eine Anlage die investieren, in der mit einer Wahrscheinlichkeit von 0,5 ein Gewinn von 6 und mit der Gegenwahrscheinlichkeit ein Verlust von -5 auftritt. Wird der Entscheidungsträger die riskante Alternative wählen? Bei der Beantwortung dieser Frage ist Risikoeinstellung der Entscheidungsträger entscheidend. Die grundsätzliche Idee ist es, die Entscheidungsträger als Erwartungsnutzenmaximierer aufzufassen. Zentral für die Einschätzung von Entscheidungen unter Unsicherheit ist demzufolge nicht die erwartete Auszahlung, sondern der erwartete Nutzen. Mit dem Konzept des Erwartungsnutzens lässt sich die Risikoeinstellung des Individuums abbilden. Der Erwartungsnutzen betrachtet nicht die Überlegung welche erwartete Auszahlung, sondern welcher Nutzen von der gewählten Alternative erwartet wird. Mit einer Wahrscheinlichkeit von 0.5 erfährt das Individuum einen Nutzen von der Auszahlung -5 [U(-5)] und mit einer Wahrscheinlichkeit 0.5 einen Nutzen von der Auszahlung 6 [U(6)]. Der erwartete Nutzen wird nunmehr über verschiedene Alternativen verglichen. Diese ist die grundlegende Logik der Erwartungsnutzentheorie. Zentral ist dabei die Gestalt der Nutzenfunktion, oder anders formuliert die Risikopräferenz des Entscheidungsträger, die wir uns im Folgenden ansehen werden.
Risikofreude
Risikofreude ist die Präferenz für ein risikoreiches Einkommen gegenüber einem sicheren Einkommen mit dem gleichen Erwartungswert. Ein solches rationales Individuum erfährt demnach aus der unsicheren Lotterie einen größeren Nutzen als aus der Auszahlung des Erwartungswertes. Der Erwartungsnutzen ist größer als der Nutzen des Erwartungswertes.
E[U] > U[E]
Grafisch ist dies durch eine konvexe Nutzenfunktion möglich. Mathematisch ist die zweite Ableitung der Nutzenfunktion größer 0:
> 0
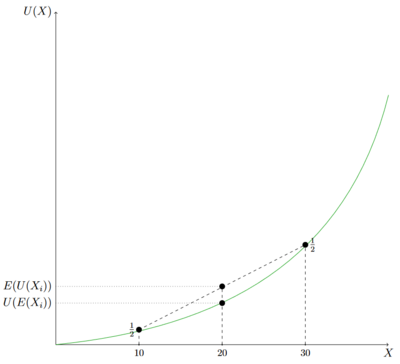
In dem grafischen Beispiel wird eine Lotterie X, X=(0.5, 10; 0.5, 30), betrachtet. Der Erwartungswert der Lotterie lautet 20 und der Nutzen des Erwartungswert liegt auf der grünen Nutzenfunktion. Mit einer Wahrscheinlichkeit von 0.5 erfährt das Individuum einen Nutzen von 10, U(10), und mit einer Wahrscheinlichkeit von 0.5 einen Nutzen von 30, U(30). Der erwartete Nutzen der Lotterie liegt auf der gestrichelten Verbindungslinie von U(10) zu U(30) und ist größer als der Nutzen des Erwartungswertes. Ist die Wahrscheinlichkeitsverteilung der beiden Auszahlungen verändert, so liegt der Erwartungsnutzen weiterhin auf der gestrichelten Verbindungslinie und ist in die Richtung der größeren Wahrscheinlichkeit verschoben. Die Risikoeinstellung des Individuums ist davon nicht betroffen.
Risikofreudige Personen haben einen zunehmenden Grenznutzen des Einkommens. Jede Einheit des Einkommens mehr erhöht das Nutzenniveau und dies stärker als die Einheit vorher. Die Chance auf ein deutlich größeres Einkommen wiegt schwerer als die Gefahr weniger Einkommen zu erhalten.
Risikoneutralität
Personen, die risikoneutral sind, sind indifferent zwischen dem unsicheren Einkommen und dem sicheren Einkommen mit demselben Erwartungswert. Der Erwartungsnutzen, also der Nutzen, der von der Lotterie erwartet werden kann, ist genauso groß wie der Nutzen des Erwartungswertes.
E[U] = U[E]
Mathematisch müssen die beiden Werte identisch sein und auf der Nutzenfunktion liegen. Dies kommt durch eine lineare Nutzenfunktion zustande. Die zweite Ableitung der Nutzenfunktion muss gleich null sein:
= 0
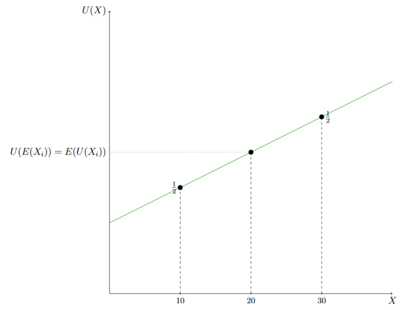
Dieselbe Lotterie X, die bereits bei der Risikofreude eine Rolle spielte, sieht mit der Nutzenfunktion einer risikoneutralen Person wie oben ersichtlich aus. Der Erwartungsnutzen ist genauso groß wie der Nutzen des Erwartungswertes (die Nutzenniveaus liegen aufeinander) und für die Person spielt es keine Rolle, ob sie den Erwartungswert der Lotterie ausgezahlt bekommt oder ob sie an der Lotterie teilnimmt.
Risikoaversion
Risikoaversion ist die Präferenz für ein sicheres Einkommen gegenüber einem risikobehafteten Einkommen mit demselben Erwartungswert. Eine risikoaverse Person erfährt demnach einen größeren Nutzen aus dem sicheren Einkommen als aus der Lotterie, die im Erwartungswert dasselbe Einkommen auszahlt. Der Nutzen des Erwartungswertes ist größer als der Erwartungsnutzen, die Nutzenfunktion ist somit konkav.
E[U] < U[E]
< 0
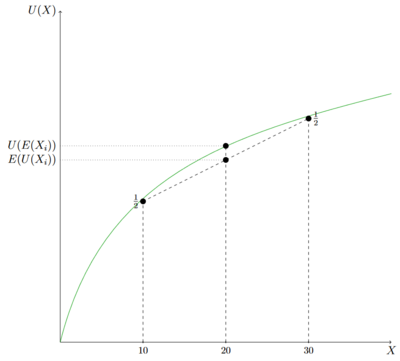
Der Erwartungsnutzen der Lotterie, der je nach Wahrscheinlichkeitsverteilung irgendwo auf der gestrichelten Verbindungslinie der beiden Nutzenniveaus liegt, liegt unter dem Nutzen, den der Erwartungswert der Lotterie bedeutet. Die Gefahr weniger zu erhalten, wiegt schwerer als die Chance mehr zu erhalten. Dies liegt am abnehmenden Grenznutzen des Einkommens. Zusätzliches Einkommen erhöht das Nutzenniveau, dies jedoch weniger als die Einheit vorher.
Sicherheitsäquivalent
Das Sicherheitsäquivalent (SÄ) ist das (sichere) Einkommen, dessen Nutzen äquivalent zu dem erwarteten Nutzen der Lotterie ist. Dementsprechend gilt U(SÄ)=E(U). Um das Sicherheitsäquivalent mathematisch herauszufinden, gilt es die Nutzenfunktion mit dem erwarteten Nutzen des unsicheren Einkommens gleichzusetzen und nach der unabhängigen Variable umzustellen. Grafisch kann das Sicherheitsäquivalent wie folgt dargestellt werden:
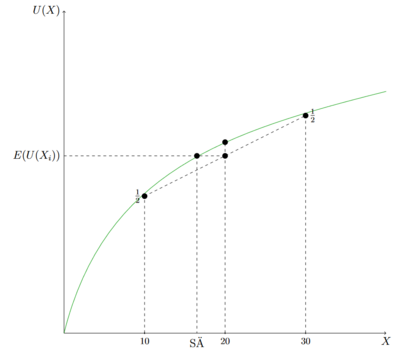
Aus den unterschiedlichen Nutzenfunktionen ergeben sich folgende Zusammenhänge:
SÄ - E[X] < 0 risikoavers
SÄ - E[X] = 0 risikoneutral
SÄ - E[X] > 0 risikofreudig
Beispiel: In einer Lohnverhandlung für einen Nebenjob wird dem Bewerber ein Gehaltsmodell vorgestellt. Mit einer Wahrscheinlichkeit von 0.5 erhält er ein Jahresgehalt von 10 und mit der Wahrscheinlichkeit von 0.5 erhält er ein Jahresgehalt von 30. Alternativ wird er gefragt, ob er dieses Gehaltsmodell gegen ein Gehalt von sicheren 5 pro Jahr eintauschen möchte. Sehr wahrscheinlich lautet seine Antwort nein. Auch bei sicheren 10 lautet seine Antwort vermutlich nein. Das Sicherheitsäquivalent ist die erste Summe, bei der der Bewerber ja sagt, da er bei dieser Summe einen gleich großen Nutzen wie durch das unsichere Gehaltsmodell erfährt.
Risikoprämie
Die Risikoprämie (RP) ist die maximale Geldsumme, die eine risikoaverse Person zur Vermeidung eines Risikos zu zahlen bereit ist. Die maximale Geldsumme ist die Differenz des Erwartungswert der Auszahlung und dem Sicherheitsäquivalent einer risikoaversen Person.
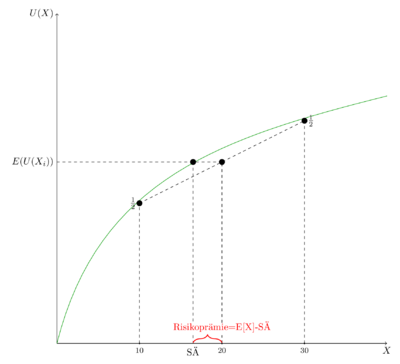
Im Beispiel von oben ist der Erwartungswert der beiden Gehaltsmöglichkeiten 20. Im Beispiel ist der Bewerber eine risikoaverse Person, weshalb die Differenz E[X] - SÄ größer null und daher positiv ist. Das Sicherheitsäquivalent ist das sichere Gehalt, das einen identisch großen Nutzen wie das unsichere Gehaltsmodell liefert (das sichere Äquivalent zur unsicheren Option). Der Bewerber ist bereit die Differenz zu zahlen, um der Unsicherheit zu entgehen und bleibt gleichzeitig auf demselben Nutzenniveau. Die Risikoprämie ist in der Abbildung unten als Differenz in rot eingezeichnet.
Versicherungsprämie
Die Versicherungsprämie ist eine Prämie, die gezahlt werden muss, um sich gegen die Unsicherheit zu versichern. Die maximale Zahlungsbereitschaft für eine solche Versicherung hängt von dem erwarteten Schaden und der Risikoeinstellung ab. Eine Person die risikoneutral ist, ist maximal bereit den erwarteten Schaden als Versicherungsprämie zu zahlen. Eine risikoaverse Person ist zum erwarteten Schaden zusätzlich bereit die Risikoprämie, also die Summe, um das Risiko zu vermeiden, zu zahlen.
VP = RP + erwarteter Schaden
Eine weitere Möglichkeit die maximale Zahlungsbereitschaft zu berechnen ist vom günstigsten Fall (das größte mögliche Einkommen) das Sicherheitsäquivalent abzuziehen.
Ein Beispiel für die Berechnung der maximalen Zahlungsbereitschaft lautet: Ein Auto kostet 100. Mit einer Wahrscheinlichkeit von 0.9 baut der Autofahrer keinen Unfall und das Auto verliert lediglich Wert aufgrund der täglichen Nutzung; der Wiederverkaufswert liegt dann bei 60. Mit einer Wahrscheinlichkeit von 0.1 baut der Autofahrer ein Unfall und das Auto verliert vollständig seinen Wert. Angenommen das Sicherheitsäquivalent liegt bei 20, wie viel würde der Autofahrer maximal für eine Versicherung zahlen?
Die erste Möglichkeit lautet VP = RP + erwarteter Schaden. Die RP berechnet sich aus der Differenz des erwarteten Vermögens und dem Sicherheitsäquivalents (54 - 20 = 34). Der erwartete Schaden berechnet sich aus 0.1 * 60 und lautet 6. Daher 34 + 6 = 40
Bei der zweiten Möglichkeit muss vom günstigsten Fall (60) das SÄ (20) abgezogen werden. Die maximale Zahlungsbereitschaft lautet 40.
MC Fragen





