Preisdiskriminierung: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
|||
| (23 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Definition== | ==Definition== | ||
| − | + | Preisdiskriminierung ist die unterschiedliche Behandlung von Konsumenten seitens der Produzenten durch eine unterschiedliche Bepreisung. Der Grad der Diskriminierung hängt mit der Möglichkeit zusammen, wie genau die Produzenten identifizieren können, wer mit welcher individuellen Zahlungsbereitschaft sein Gut nachfragt und ob unterschiedliche Preise für dasselbe Gut erlaubt sind. Außerdem muß von Seiten des Produzenten sichergestellt werden können, dass die Konsumenten nicht durch Handel untereinander die Preisdiskriminierung aushebeln können (Bedingung der Arbitragefreiheit). Preisdiskriminierung ist nur mit Marktmacht möglich. | |
__TOC__ | __TOC__ | ||
==Preisdiskriminierung ersten Grades== | ==Preisdiskriminierung ersten Grades== | ||
| − | Die Preisdiskriminierung ersten Grades wird auch als ''' | + | Die Preisdiskriminierung ersten Grades wird auch als '''perfekte Preisdiskriminierung''' bezeichnet und beschreibt die vollständige Abschöpfung der [[Konsumentenrente und Produzentenrente#Die Konsumentenrente|Konsumentenrente]]. Jeder Konsument muss seine marginale Zahlungsbereitschaft, den '''Reservationspreis''', für das Gut zahlen. <br> |
| − | ''Beispiel'': Angenommen ein Konsument ist bereit für ein Gut 10€ zu zahlen. Liegt der Marktpreis unterhalb des Reservationspreises, entsteht dem Konsumenten durch die Differenz eine Rente. Mit | + | ''Beispiel'': Angenommen ein Konsument ist bereit für ein Gut 10€ zu zahlen. Liegt der Marktpreis unterhalb des Reservationspreises, entsteht dem Konsumenten durch die Differenz eine Rente. Mit perfekter Preisdiskriminierung muss der Konsument für das Gut 10€ zahlen und die vorherige [[Konsumentenrente und Produzentenrente#Die Konsumentenrente|Konsumentenrente]] wird Teil der [[Konsumentenrente und Produzentenrente#Die Produzentenrente|Produzentenrente]]. Für diese Form der Diskriminierung muss der Produzent entsprechend genau wissen welcher Konsument das Gut nachfragt und was sein Reservationspreis ist. Außerdem muss Abitrage ausgeschlossen werden. Das heißt es darf nicht möglich sein das Gut günstig zu kaufen und an einen anderen Konsumenten mit einer höheren Zahlungsbereitschaft weiterzuverkaufen. <br> |
| − | + | Der gewinnmaximale Preis liegt dann für jede nachgefragte Menge genau auf der fallenden [[Nachfrage|Nachfragefunktion]].<br> | |
[[Datei:PD1.Grades.png|300px|rahmenlos]] <br> | [[Datei:PD1.Grades.png|300px|rahmenlos]] <br> | ||
<br clear=all> | <br clear=all> | ||
| − | Ein Konsument muss beispielsweise genau <math> p_1 </math> bezahlen und die Fläche zwischen diesem Punkt auf der Nachfragefunktion und der [[Angebot|Angebotsfunktion]] entspricht der Produzentenrente. Die Möglichkeit die [[Konsumentenrente und Produzentenrente#Die Produzentenrente|Produzentenrente]] selbst zu berechnen, bleibt unverändert: Die Fläche zwischen dem Preis und der Angebotsfunktion. Jedoch ist der Preis nicht mehr einheitlich, sondern von Konsument zu Konsument und von Menge zu Menge unterschiedlich. Diese Art der Preisdiskriminierung erzeugt keinen Wohlfahrtsverlust und stellt weiterhin ein [[Effizienz|effizientes]] [[Marktgleichgewicht im perfekten Wettbewerb|Marktgleichgewicht]] dar. <br> | + | Ein Konsument muss beispielsweise genau <math> p_1 </math> bezahlen und die Fläche zwischen diesem Punkt auf der Nachfragefunktion und der [[Angebot|Angebotsfunktion]] entspricht der Produzentenrente dieser Transaktion. Die Möglichkeit die [[Konsumentenrente und Produzentenrente#Die Produzentenrente|Produzentenrente]] selbst zu berechnen, bleibt unverändert: Die Fläche zwischen dem Preis und der Angebotsfunktion. Jedoch ist der Preis nicht mehr einheitlich, sondern von Konsument zu Konsument und von Menge zu Menge unterschiedlich. Diese Art der Preisdiskriminierung erzeugt keinen Wohlfahrtsverlust und stellt weiterhin ein [[Effizienz|effizientes]] [[Marktgleichgewicht im perfekten Wettbewerb|Marktgleichgewicht]] dar. <br> |
| − | Es ist recht offensichtlich, dass diese Form der Preisdiskriminierung schwer umzusetzen ist. Jedoch wird in der Realität durchaus versucht diesen Grad zu erreichen. | + | Es ist recht offensichtlich, dass diese Form der Preisdiskriminierung schwer umzusetzen ist. Jedoch wird in der Realität durchaus versucht diesen Grad zu erreichen. Zum Beispiel: Unterscheiden sich die Preise beim online Bestellen abhängig davon wer wann auf welchem Gerät ein Gut kaufen möchte. Dabei versuchen Algorithmen auf Grund des Gerätes (PC,Laptop etc.) und anderer Informationen (Browserverlauf) den Reservationswert zu schätzen. |
==Preisdiskriminierung zweiten Grades== | ==Preisdiskriminierung zweiten Grades== | ||
| − | Die Preisdiskriminierung zweiten Grades ist eine unvollkommene Preisdiskriminierung und wird angewendet, wenn der Anbieter die Nachfrager nicht in Gruppen einordnen und auch nicht die marginale Zahlungsbereitschaft erkennen kann. Der Anbieter bildet mehrere Preistarife, in die sich die Nachfrager selbst | + | Die Preisdiskriminierung zweiten Grades ist eine unvollkommene Preisdiskriminierung und wird angewendet, wenn der Anbieter die Nachfrager nicht in Gruppen einordnen und auch nicht die marginale Zahlungsbereitschaft erkennen kann. Der Anbieter bildet mehrere Preistarife, in die sich die Nachfrager selbst hinein selektieren. Hierbei muss der Anbieter darauf achten, dass die Tarife so gebildet werden, dass kein Nachfrager einen Anreiz hat sich in einen anderes Tarif zu wählen der nicht ihm zugedacht ist. <br> |
Beispiel sind Gasanbieter, die häufig einen Basispreis haben, der gezahlt werden muss, egal welche Leistung genutzt wird und ein Preis, der sich je nach genutzter Leistung verändert. Alle Nachfrager müssen den Basispreis bezahlen und zusätzlich pro Kilowattsunde einen Preis <math> p_1 </math>, sollte die Leistung in einer Spanne 1 liegen, einen Preis <math> p_2 </math> wenn in Spanne 2 und so weiter. <br> | Beispiel sind Gasanbieter, die häufig einen Basispreis haben, der gezahlt werden muss, egal welche Leistung genutzt wird und ein Preis, der sich je nach genutzter Leistung verändert. Alle Nachfrager müssen den Basispreis bezahlen und zusätzlich pro Kilowattsunde einen Preis <math> p_1 </math>, sollte die Leistung in einer Spanne 1 liegen, einen Preis <math> p_2 </math> wenn in Spanne 2 und so weiter. <br> | ||
| − | + | Ein weiteres Beispiel sind Flugtickets mit unterschiedlicher Flexibilität: Konsumenten, die viel Flexibilität wünschen (z.B. Geschäftsreisende) werden Tickets mit hoher Flexibilität wählen (und höheren Preisen), andere mit viel Zeit billige Tickets mit wenig Flexibilität. | |
==Preisdiskriminierung dritten Grades== | ==Preisdiskriminierung dritten Grades== | ||
| − | Die Preisdiskriminierung dritten Grades ist eine unvollkommene Preisdiskriminierung und wird an Nachfragegruppen angewendet. Sie findet Anwendung, wenn die Produzenten die Nachfrager klar einer Gruppe zuordnen können, jedoch nicht den genauen Reservationspreis der Nachfrager kennen. Angenommen es gibt nur zwei | + | Die Preisdiskriminierung dritten Grades ist eine unvollkommene Preisdiskriminierung und wird an Nachfragegruppen angewendet. Sie findet Anwendung, wenn die Produzenten die Nachfrager klar einer Gruppe zuordnen können, jedoch nicht den genauen Reservationspreis der Nachfrager kennen. Angenommen es gibt nur zwei Nachfragegruppen mit einer Nachfragegruppen-spezifischen [[Nachfrage|Nachfragefunktion]], dann maximiert der Anbieter (Monopolist) seinen Gewinn, indem er von beiden Nachfragergruppen einen unterschiedlichen Preis verlangt. <br> |
<math> \Pi=(p_1*Q_1(P)-C_1(Q_1))+(p_2*Q_2(P)-C_2(Q_2)) </math> <br> | <math> \Pi=(p_1*Q_1(P)-C_1(Q_1))+(p_2*Q_2(P)-C_2(Q_2)) </math> <br> | ||
Das Maximieren des Gewinns nach <math> p_1 </math> und <math> p_2 </math> ergibt <br> | Das Maximieren des Gewinns nach <math> p_1 </math> und <math> p_2 </math> ergibt <br> | ||
| Zeile 27: | Zeile 27: | ||
[[Datei:PD3.Grades.png|600px|rahmenlos]] <br> | [[Datei:PD3.Grades.png|600px|rahmenlos]] <br> | ||
<br clear=all> | <br clear=all> | ||
| − | Dass die [[Elastizitäten|elastischere Nachfragegruppe]] einen niedrigeren Preis zahlen muss kann neben der grafischen Darstellung oben auch rechnerisch bewiesen werden. Nach den ersten Ableitungen und Erweiterungen ergibt sich <br> | + | Dass die [[Elastizitäten|elastischere Nachfragegruppe]] einen niedrigeren Preis zahlen muss, kann neben der grafischen Darstellung oben auch rechnerisch bewiesen werden. Nach den ersten Ableitungen und Erweiterungen ergibt sich <br> |
<math> P=C'\biggl(\frac{1}{1-\frac{1}{\epsilon}}\biggr) </math> <br> bei einer positiv definierten Elastizität und <br> | <math> P=C'\biggl(\frac{1}{1-\frac{1}{\epsilon}}\biggr) </math> <br> bei einer positiv definierten Elastizität und <br> | ||
| − | <math> P=C'\biggl(\frac{1}{1+\frac{1}{\epsilon}}\biggr) </math> <br> bei einer negativ definierten Elastizität. In beiden Fällen ist der Preis größer, je unelastischer die Nachfrage ist ( | + | <math> P=C'\biggl(\frac{1}{1+\frac{1}{\epsilon}}\biggr) </math> <br> bei einer negativ definierten Elastizität. In beiden Fällen ist der Preis größer, je unelastischer die Nachfrage ist (vorausgesetzt <math> C'>0 </math>). Diese Rechnung zeigt ebenfalls, dass ein [[Vergleich Gewinnmaximum bei unterschiedlichen Marktformen|Monopolist]] niemals im unelastischen Bereich produziert, denn dort ist die Elastizität betragsmäßig kleiner als eins und es käme ein Preis geringer als die Grenzkosten heraus. <br> |
<math> \frac{p_1}{p_2}=\frac{1-\frac{1}{\epsilon_2}}{1-\frac{1}{\epsilon_1}} </math> <br> beziehungsweise <br> | <math> \frac{p_1}{p_2}=\frac{1-\frac{1}{\epsilon_2}}{1-\frac{1}{\epsilon_1}} </math> <br> beziehungsweise <br> | ||
<math> \frac{p_1}{p_2}=\frac{1+\frac{1}{\epsilon_2}}{1+\frac{1}{\epsilon_1}} </math> <br> | <math> \frac{p_1}{p_2}=\frac{1+\frac{1}{\epsilon_2}}{1+\frac{1}{\epsilon_1}} </math> <br> | ||
zeigt, dass aus <math> |\epsilon_2|>|\epsilon_1| </math>, <math> p_1>p_2 </math> folgt. <br> | zeigt, dass aus <math> |\epsilon_2|>|\epsilon_1| </math>, <math> p_1>p_2 </math> folgt. <br> | ||
| − | Die Preisdiskriminierung dritten Grades ist nur anwendbar, wenn | + | Die Preisdiskriminierung dritten Grades ist nur anwendbar, wenn Abitrage ausgeschlossen werden kann. <br> |
| − | ''Beispiel'': Ein Kino kann Studentinnen und Studenten anhand der Ausweise ihrer Universität als solche identifizieren. Außerdem nimmt es an, dass diese Nachfragegruppe eine geringere | + | ''Beispiel'': Ein Kino kann Studentinnen und Studenten anhand der Ausweise ihrer Universität als solche identifizieren. Außerdem nimmt es an, dass diese Nachfragegruppe eine geringere Zahlungsbereitschaft hat, beziehungsweise elastischer ist. Daher verlangt es für jedes Ticket nach Vorlage eines Studierendenausweises einen geringeren Preis. Bei Popcorn kann das Kino nicht ausschließen, dass die Studierenden Popcorn vergünstigt kaufen und dann teurer weiterverkaufen. Daher vergibt es auf Popcorn keinen Studierendenrabatt, aber auf die Kinotickets selbst schon. |
==MC Fragen== | ==MC Fragen== | ||
<quiz display=simple shuffleanswers=true> | <quiz display=simple shuffleanswers=true> | ||
| − | {Ein Bäcker setzt keinen festen Preis für seine Brötchen. Stattdessen entscheidet er wie viel jedem Käufer | + | {Ein Bäcker setzt keinen festen Preis für seine Brötchen. Stattdessen entscheidet er wie viel jedem Käufer ein Brötchen Wert ist und berechnet dies als Preis. Es ist den Kundinnen und Kunden nicht möglich die Brötchen weiterzuverkaufen. Der Bäcker betreibt Preisdiskriminierung |
|type="()"} | |type="()"} | ||
+ ersten Grades. | + ersten Grades. | ||
| Zeile 47: | Zeile 47: | ||
<quiz display=simple shuffleanswers=true> | <quiz display=simple shuffleanswers=true> | ||
| − | {In einem Markt hat ein Produzent eine Kostenfunktion von <math> C(Q)=\frac{1}{4}Q^2-\frac{1}{2}Q </math>. Gleichzeitig existiert eine aggregierte Nachfragefunktion von <math> Q_D=10-P </math>. Wie groß ist die Produzentenrente, die der Produzent maximal erreichen kann, vorrausgesetzt er kennt den individuellen Reservationspreis eines jeden Nachfrager und Abitrage ist ausgeschlossen? | + | {In einem Monopol-Markt hat ein Produzent eine Kostenfunktion von <math> C(Q)=\frac{1}{4}Q^2-\frac{1}{2}Q </math>. Gleichzeitig existiert eine aggregierte Nachfragefunktion von <math> Q_D=10-P </math>. Wie groß ist die Produzentenrente, die der Produzent maximal erreichen kann, vorrausgesetzt er kennt den individuellen Reservationspreis eines jeden Nachfrager und Abitrage ist ausgeschlossen? |
|type="()"} | |type="()"} | ||
| − | + | + | + 36,5 |
- 7 | - 7 | ||
- 24,5 | - 24,5 | ||
| Zeile 65: | Zeile 65: | ||
<quiz display=simple shuffleanswers=true> | <quiz display=simple shuffleanswers=true> | ||
| − | {Wie lautet der | + | {Wie lautet der gewinnmaximale Preis des Monopolisten aus der vorherigen Aufgabe, wenn er Pizza auf beiden Märkten nur zu einem Preis verkaufen darf? |
|type="()"} | |type="()"} | ||
+ <math> P^*=118,75 </math> | + <math> P^*=118,75 </math> | ||
Aktuelle Version vom 22. Februar 2024, 15:30 Uhr
Definition
Preisdiskriminierung ist die unterschiedliche Behandlung von Konsumenten seitens der Produzenten durch eine unterschiedliche Bepreisung. Der Grad der Diskriminierung hängt mit der Möglichkeit zusammen, wie genau die Produzenten identifizieren können, wer mit welcher individuellen Zahlungsbereitschaft sein Gut nachfragt und ob unterschiedliche Preise für dasselbe Gut erlaubt sind. Außerdem muß von Seiten des Produzenten sichergestellt werden können, dass die Konsumenten nicht durch Handel untereinander die Preisdiskriminierung aushebeln können (Bedingung der Arbitragefreiheit). Preisdiskriminierung ist nur mit Marktmacht möglich.
Preisdiskriminierung ersten Grades
Die Preisdiskriminierung ersten Grades wird auch als perfekte Preisdiskriminierung bezeichnet und beschreibt die vollständige Abschöpfung der Konsumentenrente. Jeder Konsument muss seine marginale Zahlungsbereitschaft, den Reservationspreis, für das Gut zahlen.
Beispiel: Angenommen ein Konsument ist bereit für ein Gut 10€ zu zahlen. Liegt der Marktpreis unterhalb des Reservationspreises, entsteht dem Konsumenten durch die Differenz eine Rente. Mit perfekter Preisdiskriminierung muss der Konsument für das Gut 10€ zahlen und die vorherige Konsumentenrente wird Teil der Produzentenrente. Für diese Form der Diskriminierung muss der Produzent entsprechend genau wissen welcher Konsument das Gut nachfragt und was sein Reservationspreis ist. Außerdem muss Abitrage ausgeschlossen werden. Das heißt es darf nicht möglich sein das Gut günstig zu kaufen und an einen anderen Konsumenten mit einer höheren Zahlungsbereitschaft weiterzuverkaufen.
Der gewinnmaximale Preis liegt dann für jede nachgefragte Menge genau auf der fallenden Nachfragefunktion.
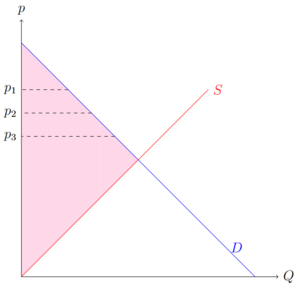
Ein Konsument muss beispielsweise genau Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1 }
bezahlen und die Fläche zwischen diesem Punkt auf der Nachfragefunktion und der Angebotsfunktion entspricht der Produzentenrente dieser Transaktion. Die Möglichkeit die Produzentenrente selbst zu berechnen, bleibt unverändert: Die Fläche zwischen dem Preis und der Angebotsfunktion. Jedoch ist der Preis nicht mehr einheitlich, sondern von Konsument zu Konsument und von Menge zu Menge unterschiedlich. Diese Art der Preisdiskriminierung erzeugt keinen Wohlfahrtsverlust und stellt weiterhin ein effizientes Marktgleichgewicht dar.
Es ist recht offensichtlich, dass diese Form der Preisdiskriminierung schwer umzusetzen ist. Jedoch wird in der Realität durchaus versucht diesen Grad zu erreichen. Zum Beispiel: Unterscheiden sich die Preise beim online Bestellen abhängig davon wer wann auf welchem Gerät ein Gut kaufen möchte. Dabei versuchen Algorithmen auf Grund des Gerätes (PC,Laptop etc.) und anderer Informationen (Browserverlauf) den Reservationswert zu schätzen.
Preisdiskriminierung zweiten Grades
Die Preisdiskriminierung zweiten Grades ist eine unvollkommene Preisdiskriminierung und wird angewendet, wenn der Anbieter die Nachfrager nicht in Gruppen einordnen und auch nicht die marginale Zahlungsbereitschaft erkennen kann. Der Anbieter bildet mehrere Preistarife, in die sich die Nachfrager selbst hinein selektieren. Hierbei muss der Anbieter darauf achten, dass die Tarife so gebildet werden, dass kein Nachfrager einen Anreiz hat sich in einen anderes Tarif zu wählen der nicht ihm zugedacht ist.
Beispiel sind Gasanbieter, die häufig einen Basispreis haben, der gezahlt werden muss, egal welche Leistung genutzt wird und ein Preis, der sich je nach genutzter Leistung verändert. Alle Nachfrager müssen den Basispreis bezahlen und zusätzlich pro Kilowattsunde einen Preis , sollte die Leistung in einer Spanne 1 liegen, einen Preis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_2 }
wenn in Spanne 2 und so weiter.
Ein weiteres Beispiel sind Flugtickets mit unterschiedlicher Flexibilität: Konsumenten, die viel Flexibilität wünschen (z.B. Geschäftsreisende) werden Tickets mit hoher Flexibilität wählen (und höheren Preisen), andere mit viel Zeit billige Tickets mit wenig Flexibilität.
Preisdiskriminierung dritten Grades
Die Preisdiskriminierung dritten Grades ist eine unvollkommene Preisdiskriminierung und wird an Nachfragegruppen angewendet. Sie findet Anwendung, wenn die Produzenten die Nachfrager klar einer Gruppe zuordnen können, jedoch nicht den genauen Reservationspreis der Nachfrager kennen. Angenommen es gibt nur zwei Nachfragegruppen mit einer Nachfragegruppen-spezifischen Nachfragefunktion, dann maximiert der Anbieter (Monopolist) seinen Gewinn, indem er von beiden Nachfragergruppen einen unterschiedlichen Preis verlangt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Pi=(p_1*Q_1(P)-C_1(Q_1))+(p_2*Q_2(P)-C_2(Q_2)) }
Das Maximieren des Gewinns nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1 }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_2 }
ergibt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle MR_1=GK }
und
Dementsprechend muss gelten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle MR_1=MR_2=GK }
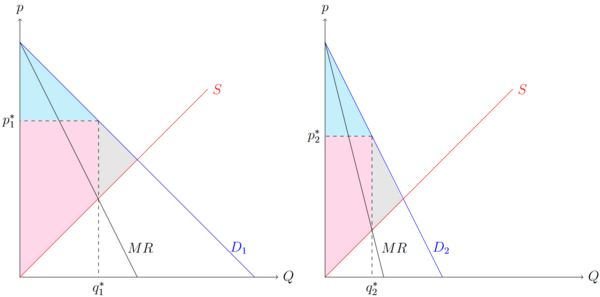
Dass die elastischere Nachfragegruppe einen niedrigeren Preis zahlen muss, kann neben der grafischen Darstellung oben auch rechnerisch bewiesen werden. Nach den ersten Ableitungen und Erweiterungen ergibt sich
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P=C'\biggl(\frac{1}{1-\frac{1}{\epsilon}}\biggr) }
bei einer positiv definierten Elastizität und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P=C'\biggl(\frac{1}{1+\frac{1}{\epsilon}}\biggr) }
bei einer negativ definierten Elastizität. In beiden Fällen ist der Preis größer, je unelastischer die Nachfrage ist (vorausgesetzt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C'>0 }
). Diese Rechnung zeigt ebenfalls, dass ein Monopolist niemals im unelastischen Bereich produziert, denn dort ist die Elastizität betragsmäßig kleiner als eins und es käme ein Preis geringer als die Grenzkosten heraus.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{p_1}{p_2}=\frac{1-\frac{1}{\epsilon_2}}{1-\frac{1}{\epsilon_1}} }
beziehungsweise
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{p_1}{p_2}=\frac{1+\frac{1}{\epsilon_2}}{1+\frac{1}{\epsilon_1}} }
zeigt, dass aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |\epsilon_2|>|\epsilon_1| }
, folgt.
Die Preisdiskriminierung dritten Grades ist nur anwendbar, wenn Abitrage ausgeschlossen werden kann.
Beispiel: Ein Kino kann Studentinnen und Studenten anhand der Ausweise ihrer Universität als solche identifizieren. Außerdem nimmt es an, dass diese Nachfragegruppe eine geringere Zahlungsbereitschaft hat, beziehungsweise elastischer ist. Daher verlangt es für jedes Ticket nach Vorlage eines Studierendenausweises einen geringeren Preis. Bei Popcorn kann das Kino nicht ausschließen, dass die Studierenden Popcorn vergünstigt kaufen und dann teurer weiterverkaufen. Daher vergibt es auf Popcorn keinen Studierendenrabatt, aber auf die Kinotickets selbst schon.
MC Fragen
