Externalitäten und Internalisierung: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
|||
| (31 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
==Positive Externalitäten== | ==Positive Externalitäten== | ||
| − | Positive Externalitäten führen dazu, dass zu wenig produziert wird. Ein mögliches Beispiel sind Renovierungsarbeiten an einem Haus. Die Hausbesitzer erfahren einen Nutzen (Utility) aus der Renovierung ihres Hauses. Der Garten, die Einfahrt und auch die komplette Hausfassade müssen modernisiert werden, wodurch Kosten entstehen | + | Positive Externalitäten führen dazu, dass zu wenig produziert wird. Ein mögliches Beispiel sind Renovierungsarbeiten an einem Haus. Die Hausbesitzer erfahren einen Nutzen (Utility) aus der Renovierung ihres Hauses. Der Garten, die Einfahrt und auch die komplette Hausfassade müssen modernisiert werden, wodurch Kosten entstehen. Die [[Kostenarten#Grenzkosten|Grenzkosten]] für die Renovierung sollen im Beispiel steigend sein. Je mehr renoviert wird, desto besser ist es für die Hausbesitzer. Aber jede Stunde mehr bringt weniger zusätzlichen Nutzen, es liegt also ein [[Nutzentheorie|abnehmender Grenznutzen]] (Marginal Utility=MU) vor. Die Hausbesitzer beauftragen einen Dienstleister für die Renovierungsarbeiten so lange, bis sie die nächste Stunde Arbeit mehr kostet, als ihnen zusätzlichen Nutzen bringt. Die Hausnachbarn, profitieren allerdings auch von der Renovierung, da sie hierdurch zum Beispiel aufgrund der schöner werdenden Aussicht lieber in ihrem Garten sitzen. Da sie einen Nutzen aus der Renovierung erfahren, bringt ihnen jede zusätzliche Stunde Arbeit des Dienstleisters mehr Nutzen (MU). Dieser Nutzen wird jedoch nicht in der Entscheidung einbezogen, denn nur die Hausbesitzer achten auf ihr Grenzkosten-Grenznutzenverhältnis. Der soziale Nutzen (SU) stellt sich aus dem Nutzen der Hausbesitzer plus dem Nutzen der Nachbarn (Externer Nutzen=EU) zusammen. <br> |
SU = U + EU <br> | SU = U + EU <br> | ||
Daraus folgt im sozialen Optimum: <br> | Daraus folgt im sozialen Optimum: <br> | ||
SMU=GK <br> | SMU=GK <br> | ||
MU + MEU = GK <br> | MU + MEU = GK <br> | ||
| − | Wie in der Abbildung zu sehen ist liegt die produzierte Menge <math display="inline"> q_{1} </math> unter der sozial optimalen Menge <math display="inline"> q^{*} </math>. Im Fall von steigenden Grenzkosten lässt sich | + | Der SMU (Social Marginal Utility) ist der soziale Grenznutzen. Wie in der Abbildung zu sehen ist liegt die produzierte Menge <math display="inline"> q_{1} </math> unter der sozial optimalen Menge <math display="inline"> q^{*} </math>. Im Fall von steigenden Grenzkosten lässt sich sehen, dass der tatsächliche Preis <math> p_1 </math> unter dem sozial optimalen Preis <math display="inline"> p^{*} </math> liegt. Es sind auch Szenrien vorstellbar, in denen der externe Effekt kostant ist. Auch die Grenzkosten könnten theoretisch konstant sein. <br> |
| − | [[Datei:PositiveExternalitäten.png| | + | [[Datei:PositiveExternalitäten.png|501px|rahmenlos]] |
==Negative Externalitäten== | ==Negative Externalitäten== | ||
| − | Negative Externalitäten führen dazu, dass zu einem zu niedrigen Preis eine zu große Menge produziert wird. Ein mögliches Beispiel ist eine Firma, die in ihrer Produktion Abgase unkontrolliert in die Luft stößt. Dadurch entsteht den umliegenden Haushalten ein Disnutzen, beziehungsweise entstehen ihnen Kosten um sich vor den Abgasen zu schützen (z.B. Finanzierung eines Aufforstungsprogramms, damit Bäume die Abgase filtern). Diese Kosten fallen pro produzierter Einheit an und die Reduzierung von jeder weiteren Einheit der Abgase wird immer teurer. In der Abbildung unten soll die EMC (external Marginal Costs) Kurve diese Kosten widerspiegeln. Die Firma selbst zahlt diese Kosten jedoch nicht, sondern zahlt nur die Kosten, die in der Produktion direkt entstehen (MC Kurve). Diese [[Grenzkosten]] bilden die [[Angebot|Angebotsfunktion]], die zusammen mit der [[Nachfrage]] einen Marktpreis <math display="inline"> P_{1} </math> und eine Gleichgewichtsmenge <math display="inline"> Q_{1} </math> bilden. Dieses [[Marktgleichgewicht im perfekten Wettbewerb|Marktgleichgewicht]] ist jedoch nicht effizient, da die Grenzkosten, die in der Bestimmung des Gleichgewichts als Angebotskurve herangezogen werden, in Wahrheit größer sind. Die tatsächliche Grenzkostenkurve ist in der SMC (Social Marginal Costs) Kurve dargestellt. Diese Kurve preist die negative Externalität, die die Haushalte negativ betrifft, ein. Die gesellschaftliche Angebotskurve besteht aus den (privaten) Grenzkosten der Firma und den Grenzkosten der Haushalte. Im alten Marktgleichgewicht wird eine zu große Menge zu einem zu niedrigen Preis produziert, wodurch eine Wohlfahrtsverlust (in der grauen Fläche gekennzeichnet) entsteht; das alte Marktgleichgewicht ist nicht [[Effizienz|effizient]]. <br> | + | Negative Externalitäten führen dazu, dass zu einem zu niedrigen Preis eine zu große Menge produziert wird. Ein mögliches Beispiel ist eine Firma, die in ihrer Produktion Abgase unkontrolliert in die Luft stößt. Dadurch entsteht den umliegenden Haushalten ein Disnutzen, beziehungsweise entstehen ihnen Kosten um sich vor den Abgasen zu schützen (z.B. Finanzierung eines Aufforstungsprogramms, damit Bäume die Abgase filtern). Diese Kosten fallen pro produzierter Einheit an und die Reduzierung von jeder weiteren Einheit der Abgase wird immer teurer. In der Abbildung unten soll die EMC (external Marginal Costs) Kurve diese Kosten widerspiegeln. Die Firma selbst zahlt diese Kosten jedoch nicht, sondern zahlt nur die Kosten, die in der Produktion direkt entstehen (MC Kurve). Diese [[Kostenarten#Grenzkosten|Grenzkosten]] bilden die [[Angebot|Angebotsfunktion]], die zusammen mit der [[Nachfrage]] einen Marktpreis <math display="inline"> P_{1} </math> und eine Gleichgewichtsmenge <math display="inline"> Q_{1} </math> bilden. Dieses [[Marktgleichgewicht im perfekten Wettbewerb|Marktgleichgewicht]] ist jedoch nicht effizient, da die Grenzkosten, die in der Bestimmung des Gleichgewichts als Angebotskurve herangezogen werden, in Wahrheit größer sind. Die tatsächliche Grenzkostenkurve ist in der SMC (Social Marginal Costs) Kurve dargestellt. Diese Kurve preist die negative Externalität, die die Haushalte negativ betrifft, ein. Die gesellschaftliche Angebotskurve besteht aus den (privaten) Grenzkosten der Firma und den Grenzkosten der Haushalte. Im alten Marktgleichgewicht wird eine zu große Menge zu einem zu niedrigen Preis produziert, wodurch eine Wohlfahrtsverlust (in der grauen Fläche gekennzeichnet) entsteht; das alte Marktgleichgewicht ist nicht [[Effizienz|effizient]]. <br> |
| − | [[Datei:NegativeExternalitäten.png| | + | [[Datei:NegativeExternalitäten.png|501px|rahmenlos]] |
==Internalisierung== | ==Internalisierung== | ||
| − | Externalitäten führen zu nicht [[Effizienz|effizienten]] [[Marktgleichgewicht im perfekten Wettbewerb|Marktgleichgewichten]], da entweder zu viel oder zu wenig zu einem zu geringen oder zu einem zu hohen Preis produziert wird. Externalitäten stellen also Beispiele für [[Zusammenfassung Marktversagen|Marktversagen]] dar, für die es im Falle von Externalitäten verschiedene Möglichkeiten gibt diese durch Internalisierung zu verhindern. <br> | + | Externalitäten führen zu nicht [[Effizienz|effizienten]] [[Marktgleichgewicht im perfekten Wettbewerb|Marktgleichgewichten]], da entweder zu viel (im Falle negativer Externalitäten) oder zu wenig (im Falle positiver Externalitäten) zu einem zu geringen oder zu einem zu hohen Preis produziert wird. Externalitäten stellen also Beispiele für [[Zusammenfassung Marktversagen|Marktversagen]] dar, für die es im Falle von Externalitäten verschiedene Möglichkeiten gibt diese durch Internalisierung zu verhindern. <br> |
<br> | <br> | ||
'''Pigou Steuer (staatliche Eingriffe)''' <br> | '''Pigou Steuer (staatliche Eingriffe)''' <br> | ||
| − | Im Falle von negativen Externlitäten ist die private Gleichgewichtsmenge größer als die soziale Gleichgewichtsmenge und der Preis ist im privaten Gleichgewicht niedriger als im sozialen. Dies liegt an Kosten, die in der Angebotskurve nicht eingepreist sind. Eine [[Steuern|Mengensteuer]], die die Angebotskurve um genau die nicht eingepreisten Kosten pro Einheit nach oben verschiebt, kann den Markt effizient gestalten. Fällt in der Produktion von einer produzierten Einheit zum Beispiel Abgase an, deren Entfernung aus der Atmosphäre eine Summe | + | Im Falle von negativen Externlitäten ist die private Gleichgewichtsmenge größer als die soziale Gleichgewichtsmenge und der Preis ist im privaten Gleichgewicht niedriger als im sozialen. Dies liegt an Kosten, die in der Angebotskurve nicht eingepreist sind. Eine [[Eingriffe in das Marktgleichgewicht#Steuern|Mengensteuer]], die die Angebotskurve um genau die nicht eingepreisten Kosten pro Einheit nach oben verschiebt, kann den Markt effizient gestalten. Fällt in der Produktion von einer produzierten Einheit zum Beispiel Abgase an, deren Entfernung aus der Atmosphäre eine Summe t kostet, so kann eine Mengensteuer in der Höhe von t das Gleichgewicht effizient gestalten. Diese Steuer wird Pigou Steuer genannt. <br> |
Hierbei ist allerdings zu beachten, dass die anfallenden Kosten genau bemessbar und die Kostenstruktur der produzierenden Unternehmen bekannt sind. Andernfalls könnte die Mengensteuer häufig zu hoch oder zu niedrig ausfallen. <br> | Hierbei ist allerdings zu beachten, dass die anfallenden Kosten genau bemessbar und die Kostenstruktur der produzierenden Unternehmen bekannt sind. Andernfalls könnte die Mengensteuer häufig zu hoch oder zu niedrig ausfallen. <br> | ||
| − | [[Datei:PigouSteuer.png| | + | [[Datei:PigouSteuer.png|402px|rahmenlos]] <br clear="all"> |
| − | Um positive Externalitäten in einer ähnlichen Art und Weise zu interalisieren muss es das Ziel sein die Angebotskurve der Unternehmen nach unten zu verschieben. | + | Um positive Externalitäten in einer ähnlichen Art und Weise zu interalisieren muss es das Ziel sein die Angebotskurve der Unternehmen nach unten zu verschieben. Hierzu können negative Steuern, also [[Eingriffe in das Marktgleichgewicht|Subventionen]], dienen. |
<br> | <br> | ||
<br> | <br> | ||
| Zeile 33: | Zeile 33: | ||
Gehen wir zur Analyse Zertifikathandels von einem Szenario aus, in dem Firma X alle Zertifikate hat und somit vollständig die erlaute Menge ausstößt. In diesem Fall müsste Firma Y ihren Ausstoß zu hohen Kosten vollständig zu reduzieren. In diesem Punkt wäre Firma Y bereit Firma X bereit maximal so viel für den Ausstoß einer Einheit zu bezahlen, wie es kostet diese einzusparen. Solange Firma X mehr für diese Menge bekommt, als es sie kostet diese Menge einzusparen, würde X tatsächlich eine Einheit Ausstoß "verkaufen". In anderen Worten: Y bezahlt X um eine Einheit ausstoßen zu können und zahlt dafür einen Preis, der kleiner oder gleich den Kosten der Reduktion dieser Einheit ist. Solange die Kosten der Ausstoßeinsparung von Y größer als denen von X ist, reduziert X seinen AUsstoß und wird dafür von Y bezahlt. Dies findet solange statt, bis die Ausstoßeinsparung jeder weiteren Einheit für X genauso teuer ist wie für Y. In diesem Schnittpunkt der beiden Kostenfunktionen entsteht ein Marktpreis für den Zertifikathandel. In der Abbildung zu erkennen ist zudem die [[Effizienz|effiziente]] Ausstoßmenge der beiden Firmen. Firma X hat höhere Reduzierungskosten und stößt im Schnittpunkt daher mehr aus als Y, die geringere Reduzierungskosten hat. <br> | Gehen wir zur Analyse Zertifikathandels von einem Szenario aus, in dem Firma X alle Zertifikate hat und somit vollständig die erlaute Menge ausstößt. In diesem Fall müsste Firma Y ihren Ausstoß zu hohen Kosten vollständig zu reduzieren. In diesem Punkt wäre Firma Y bereit Firma X bereit maximal so viel für den Ausstoß einer Einheit zu bezahlen, wie es kostet diese einzusparen. Solange Firma X mehr für diese Menge bekommt, als es sie kostet diese Menge einzusparen, würde X tatsächlich eine Einheit Ausstoß "verkaufen". In anderen Worten: Y bezahlt X um eine Einheit ausstoßen zu können und zahlt dafür einen Preis, der kleiner oder gleich den Kosten der Reduktion dieser Einheit ist. Solange die Kosten der Ausstoßeinsparung von Y größer als denen von X ist, reduziert X seinen AUsstoß und wird dafür von Y bezahlt. Dies findet solange statt, bis die Ausstoßeinsparung jeder weiteren Einheit für X genauso teuer ist wie für Y. In diesem Schnittpunkt der beiden Kostenfunktionen entsteht ein Marktpreis für den Zertifikathandel. In der Abbildung zu erkennen ist zudem die [[Effizienz|effiziente]] Ausstoßmenge der beiden Firmen. Firma X hat höhere Reduzierungskosten und stößt im Schnittpunkt daher mehr aus als Y, die geringere Reduzierungskosten hat. <br> | ||
<br> | <br> | ||
| − | '''[[Coase | + | '''[[Coase Theorem]]''' <br> |
| − | + | Das Coase Theorem besagt, dass unter Abwesenheit von Einkommenseffekten und Transaktionskosten und unter der Annahme der symmetrischen Informationen durch Verhandlungen wenige Parteien zu einer pareto effiziente Allokation kommen können. Dadurch wird das Externalitätenproblem, bei dem die negativen Externalitäten einer Partei die anderen Parteien beeinflussen, gelöst. Die genaue Verteilung der Eigentumsrechte ist aus allokativer Sicht irrelevant (es wird in beiden Fällen gleich viel verschmutzt). Die Verteilung der Eigentumsrechte hat demnach lediglich Verteilungseffekte. Im simpelsten Modell haben zwei Unternehmen einen Gewinn und eines der beiden Unternehmen bekommt Eigentumsrechte zugesprochen. Das Unternehmen mit den Eigentumsrechten kann entscheiden, ob das andere Unternehmen produzieren darf oder nicht. Die Entscheidug beeinflusst den eigenen Gewinn des Unternehmens. Daher nimmt es in den Verhandlungen nur Angebote an, die es nicht schlechter stellen als ohne Verhandlungen. <br> | |
| − | + | {| class="wikitable" | |
| + | |- | ||
| + | ! Eigentumsrecht bei | ||
| + | ! Gewinn C | ||
| + | ! Gewinn F | ||
| + | ! gesamt<br /> | ||
| + | ! resultierende Allokation | ||
| + | |- | ||
| + | | C | ||
| + | | <span style="color:#009999"> 40 </span> | ||
| + | | 60-<span style="color:#009999"> 40 </span> | ||
| + | | 60 | ||
| + | | C schließt<br /> | ||
| + | |- | ||
| + | | F | ||
| + | | 0 | ||
| + | | 60 | ||
| + | | 60 | ||
| + | | C schließt | ||
| + | |} | ||
| + | Angenommen ein Unternehmen C macht einen Gewinn von 40, wenn es produziert und ein Unternehmen F aufgrund von negativen Externalitäten 0. Wenn C nicht produziert, macht F einen Gewinn von 60. Die Tabelle oben verdeutlicht, dass unabhängig wer die Eigentumsrechte hat, rational geführte Verhandlungen zu einer pareto effizienten Allokation führen. <br> | ||
| + | Für eine ausführlichere Beschreibung und weitere Szenarien, [[Coase Theorem|hier]]. | ||
==MC Fragen== | ==MC Fragen== | ||
<quiz display=simple shuffleanswers=true> | <quiz display=simple shuffleanswers=true> | ||
| − | { | + | {Auf einem Markt für Honig sind die Nachfrager bereit ihren Grenznutzen für ein Glas Honig zu zahlen. Die Nachfragefunktion lautet <math> Q_D(P)=43-\frac{1}{2}P </math>. Die Angebotsfunktion der Honigbauern lautet <math> Q_S(P)=2P </math>. Da das Bestäuben von Blüten neben der Honigproduktion auch die Früchte von Nutzpflanzen ermöglicht, entsteht ein zusätzlicher Nutzen, der von der Gesellschaft bisher nicht eingepreist wurde. Angenommen durch jedes verkaufte Glas Honig entsteht ein zusätzlicher Nutzen, der mit 4 Euro beziffert werden kann. Wie lautet das soziale Optimum? |
|type="()"} | |type="()"} | ||
| − | + | + | + <math> P^*=18 </math> und <math> Q^*=36</math>. |
| − | - | + | - <math> P^*=15 </math> und <math> Q^*=30</math>. |
| − | - | + | - <math> P^*=21 </math> und <math> Q^*=42</math>. |
| − | - | + | - <math> P^*=16 </math> und <math> Q^*=32</math>. |
| + | </quiz> | ||
| + | |||
| + | <quiz display=simple shuffleanswers=true> | ||
| + | {Die aggregierte Nachfragefunktion für einen Lebkuchenmarkt lautet <math> P(Q_D)=100-8Q_D </math>. Die Angebotsfunktion lautet <math> P(Q_S)=2Q_S </math>. Bei der Produktion von Lebkuchen fallen negative Externalitäten an, die nicht in der Angebotsfunktion inkludiert werden. Ein sozialer optimaler Preis wäre 36. Wie groß muss eine Mengensteuer sein, um die Externalitäten zu internalisieren? | ||
| + | |type="()"} | ||
| + | + t=20 | ||
| + | - t=10 | ||
| + | - t=4 | ||
| + | - t=16 | ||
| + | </quiz> | ||
| + | |||
| + | |||
| + | <quiz display=simple shuffleanswers=true> | ||
| + | {Welche Aussage bezüglich dem Handel mit Zertifikaten stimmt '''nicht'''? (Annahme der effizienten Allokation) | ||
| + | |type="()"} | ||
| + | + Der Zertifikatehandel setzt für ein effizientes Gleichgewicht vorraus, dass die Institution, die die Zertifikate ausgibt, über die Produktionsstruktur der Unternehmen informiert ist. | ||
| + | - Der Preis der Zertifikate beeinflusst nicht, über welchen Rahmen die Zertifikate gehen (Im Kontext der CO2 Zertifikate bestimmt der Preis nicht, wie viel pro Zertifikat ausgestoßen werden darf) | ||
| + | - Im Gleichgewicht des Marktes für Zertifikate, ist der Preis für die Nutzung eines Zertifikates genauso groß wie die Kosten, die durch Verhinderung der Externalitäten entstehen. | ||
| + | - Die effiziente Allokation stellt ein soziales Optimum dar. | ||
</quiz> | </quiz> | ||
Aktuelle Version vom 22. März 2024, 16:31 Uhr
Definition
Externalitäten beschreiben Handlungen von Produzenten oder Konsumenten, welche anderen Marktteilnehmer betreffen ohne jedoch im Marktgleichgewicht eingepreist zu sein. Wir unterscheiden hierbei zwischen positiven und negativen Externalitäten.
Positive Externalitäten
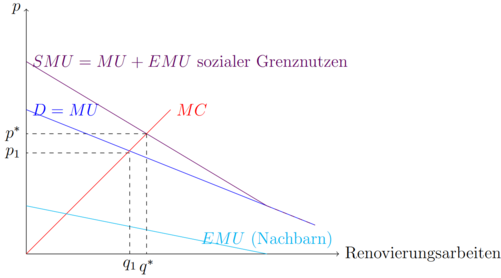
Positive Externalitäten führen dazu, dass zu wenig produziert wird. Ein mögliches Beispiel sind Renovierungsarbeiten an einem Haus. Die Hausbesitzer erfahren einen Nutzen (Utility) aus der Renovierung ihres Hauses. Der Garten, die Einfahrt und auch die komplette Hausfassade müssen modernisiert werden, wodurch Kosten entstehen. Die Grenzkosten für die Renovierung sollen im Beispiel steigend sein. Je mehr renoviert wird, desto besser ist es für die Hausbesitzer. Aber jede Stunde mehr bringt weniger zusätzlichen Nutzen, es liegt also ein abnehmender Grenznutzen (Marginal Utility=MU) vor. Die Hausbesitzer beauftragen einen Dienstleister für die Renovierungsarbeiten so lange, bis sie die nächste Stunde Arbeit mehr kostet, als ihnen zusätzlichen Nutzen bringt. Die Hausnachbarn, profitieren allerdings auch von der Renovierung, da sie hierdurch zum Beispiel aufgrund der schöner werdenden Aussicht lieber in ihrem Garten sitzen. Da sie einen Nutzen aus der Renovierung erfahren, bringt ihnen jede zusätzliche Stunde Arbeit des Dienstleisters mehr Nutzen (MU). Dieser Nutzen wird jedoch nicht in der Entscheidung einbezogen, denn nur die Hausbesitzer achten auf ihr Grenzkosten-Grenznutzenverhältnis. Der soziale Nutzen (SU) stellt sich aus dem Nutzen der Hausbesitzer plus dem Nutzen der Nachbarn (Externer Nutzen=EU) zusammen.
SU = U + EU
Daraus folgt im sozialen Optimum:
SMU=GK
MU + MEU = GK
Der SMU (Social Marginal Utility) ist der soziale Grenznutzen. Wie in der Abbildung zu sehen ist liegt die produzierte Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q_{1} }
unter der sozial optimalen Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle q^{*} }
. Im Fall von steigenden Grenzkosten lässt sich sehen, dass der tatsächliche Preis unter dem sozial optimalen Preis liegt. Es sind auch Szenrien vorstellbar, in denen der externe Effekt kostant ist. Auch die Grenzkosten könnten theoretisch konstant sein.
Negative Externalitäten
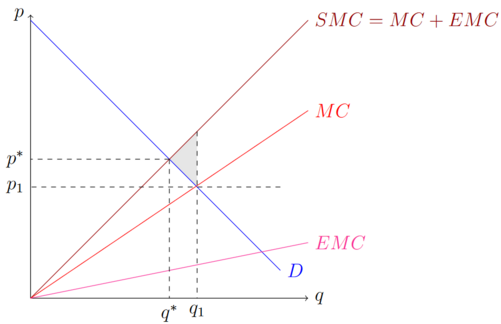
Negative Externalitäten führen dazu, dass zu einem zu niedrigen Preis eine zu große Menge produziert wird. Ein mögliches Beispiel ist eine Firma, die in ihrer Produktion Abgase unkontrolliert in die Luft stößt. Dadurch entsteht den umliegenden Haushalten ein Disnutzen, beziehungsweise entstehen ihnen Kosten um sich vor den Abgasen zu schützen (z.B. Finanzierung eines Aufforstungsprogramms, damit Bäume die Abgase filtern). Diese Kosten fallen pro produzierter Einheit an und die Reduzierung von jeder weiteren Einheit der Abgase wird immer teurer. In der Abbildung unten soll die EMC (external Marginal Costs) Kurve diese Kosten widerspiegeln. Die Firma selbst zahlt diese Kosten jedoch nicht, sondern zahlt nur die Kosten, die in der Produktion direkt entstehen (MC Kurve). Diese Grenzkosten bilden die Angebotsfunktion, die zusammen mit der Nachfrage einen Marktpreis und eine Gleichgewichtsmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Q_{1} }
bilden. Dieses Marktgleichgewicht ist jedoch nicht effizient, da die Grenzkosten, die in der Bestimmung des Gleichgewichts als Angebotskurve herangezogen werden, in Wahrheit größer sind. Die tatsächliche Grenzkostenkurve ist in der SMC (Social Marginal Costs) Kurve dargestellt. Diese Kurve preist die negative Externalität, die die Haushalte negativ betrifft, ein. Die gesellschaftliche Angebotskurve besteht aus den (privaten) Grenzkosten der Firma und den Grenzkosten der Haushalte. Im alten Marktgleichgewicht wird eine zu große Menge zu einem zu niedrigen Preis produziert, wodurch eine Wohlfahrtsverlust (in der grauen Fläche gekennzeichnet) entsteht; das alte Marktgleichgewicht ist nicht effizient.
Internalisierung
Externalitäten führen zu nicht effizienten Marktgleichgewichten, da entweder zu viel (im Falle negativer Externalitäten) oder zu wenig (im Falle positiver Externalitäten) zu einem zu geringen oder zu einem zu hohen Preis produziert wird. Externalitäten stellen also Beispiele für Marktversagen dar, für die es im Falle von Externalitäten verschiedene Möglichkeiten gibt diese durch Internalisierung zu verhindern.
Pigou Steuer (staatliche Eingriffe)
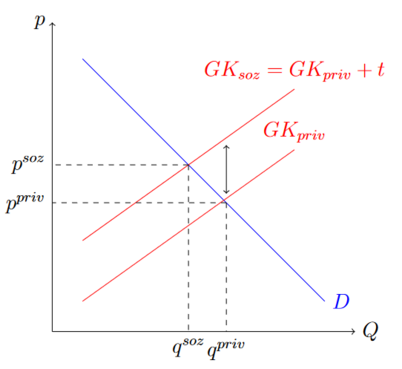
Im Falle von negativen Externlitäten ist die private Gleichgewichtsmenge größer als die soziale Gleichgewichtsmenge und der Preis ist im privaten Gleichgewicht niedriger als im sozialen. Dies liegt an Kosten, die in der Angebotskurve nicht eingepreist sind. Eine Mengensteuer, die die Angebotskurve um genau die nicht eingepreisten Kosten pro Einheit nach oben verschiebt, kann den Markt effizient gestalten. Fällt in der Produktion von einer produzierten Einheit zum Beispiel Abgase an, deren Entfernung aus der Atmosphäre eine Summe t kostet, so kann eine Mengensteuer in der Höhe von t das Gleichgewicht effizient gestalten. Diese Steuer wird Pigou Steuer genannt.
Hierbei ist allerdings zu beachten, dass die anfallenden Kosten genau bemessbar und die Kostenstruktur der produzierenden Unternehmen bekannt sind. Andernfalls könnte die Mengensteuer häufig zu hoch oder zu niedrig ausfallen.
Um positive Externalitäten in einer ähnlichen Art und Weise zu interalisieren muss es das Ziel sein die Angebotskurve der Unternehmen nach unten zu verschieben. Hierzu können negative Steuern, also Subventionen, dienen.
Zertifikate
Eine weitere Möglichkeit um negative Externalitäten zu internalisieren sind Zertifikate. Bei den Zertifikaten wird die zum Beispiel maximal zugelassene Menge an ausgestoßenen Abgasen festgelegt und als Zertifikate ausgegeben. Zertifikate erlauben eine gewisse Menge an Abgasen auszustoßen, sollte jedoch mehr ausgestoßen werden drohen wirksame Strafen. Der Vorteil von Zertifikaten gegenüber einfachen Beschränkungen liegt darin, dass sie in der Regel handelbar sind. Sollte ein Unternehmen weniger ausstoßen als sie laut ihren Zertifikaten könnten, kann es die übrigen Zertifikate an andere Unternehmen verkaufen. Wenn die Menge an Abgasen so reglementiert ist, dass alle Unternehmen abgasärmer produzieren müssen, können Zertifikate trotzdem zu einem effizienten Handel führen. ALs Beispiel soll untenstehende Grafik dienen:
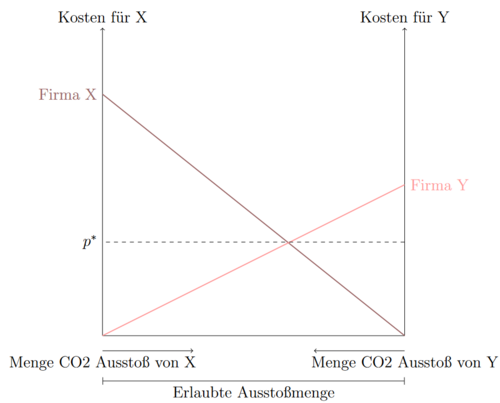
Die komplette Breite der x-Achse soll der erlaubten Ausstoßmenge an Abgasen entsprechen. Die Ausstoßmenge an Abgasen von Firma X steigt je weiter rechts wir uns befinden, die von Firma Y je weiter links. Je mehr X ausstößt, desto weniger kann jedoch Y ausstoßen. Auf den beiden y-Achsen sind die Kosten der beiden Firmen abgetrafegn, die es ihnen kostet eine Einheit weniger auszustoßen. Nehmen wir hier als Beispiel Firma X: Ganz rechts auf der x-Achse stoßt X viele Abgase aus. An dieser Stelle kostet es X kaum etwas die Abgase zu reduzieren. Je weniger X ausstößt, desto teurer wird es allerdings eine weitere Einheit des Abgases einzusparen. Ähnlich verhält es sich bei Firma Y. Vergleicht man die beiden Kostenfunktionen, so fällt auf, dass die der Firma Y deutlich flacher verläuft. Fimra Y kann also kostengünstiger den Ausstoß von Abgasen reduzieren.
Gehen wir zur Analyse Zertifikathandels von einem Szenario aus, in dem Firma X alle Zertifikate hat und somit vollständig die erlaute Menge ausstößt. In diesem Fall müsste Firma Y ihren Ausstoß zu hohen Kosten vollständig zu reduzieren. In diesem Punkt wäre Firma Y bereit Firma X bereit maximal so viel für den Ausstoß einer Einheit zu bezahlen, wie es kostet diese einzusparen. Solange Firma X mehr für diese Menge bekommt, als es sie kostet diese Menge einzusparen, würde X tatsächlich eine Einheit Ausstoß "verkaufen". In anderen Worten: Y bezahlt X um eine Einheit ausstoßen zu können und zahlt dafür einen Preis, der kleiner oder gleich den Kosten der Reduktion dieser Einheit ist. Solange die Kosten der Ausstoßeinsparung von Y größer als denen von X ist, reduziert X seinen AUsstoß und wird dafür von Y bezahlt. Dies findet solange statt, bis die Ausstoßeinsparung jeder weiteren Einheit für X genauso teuer ist wie für Y. In diesem Schnittpunkt der beiden Kostenfunktionen entsteht ein Marktpreis für den Zertifikathandel. In der Abbildung zu erkennen ist zudem die effiziente Ausstoßmenge der beiden Firmen. Firma X hat höhere Reduzierungskosten und stößt im Schnittpunkt daher mehr aus als Y, die geringere Reduzierungskosten hat.
Coase Theorem
Das Coase Theorem besagt, dass unter Abwesenheit von Einkommenseffekten und Transaktionskosten und unter der Annahme der symmetrischen Informationen durch Verhandlungen wenige Parteien zu einer pareto effiziente Allokation kommen können. Dadurch wird das Externalitätenproblem, bei dem die negativen Externalitäten einer Partei die anderen Parteien beeinflussen, gelöst. Die genaue Verteilung der Eigentumsrechte ist aus allokativer Sicht irrelevant (es wird in beiden Fällen gleich viel verschmutzt). Die Verteilung der Eigentumsrechte hat demnach lediglich Verteilungseffekte. Im simpelsten Modell haben zwei Unternehmen einen Gewinn und eines der beiden Unternehmen bekommt Eigentumsrechte zugesprochen. Das Unternehmen mit den Eigentumsrechten kann entscheiden, ob das andere Unternehmen produzieren darf oder nicht. Die Entscheidug beeinflusst den eigenen Gewinn des Unternehmens. Daher nimmt es in den Verhandlungen nur Angebote an, die es nicht schlechter stellen als ohne Verhandlungen.
| Eigentumsrecht bei | Gewinn C | Gewinn F | gesamt |
resultierende Allokation |
|---|---|---|---|---|
| C | 40 | 60- 40 | 60 | C schließt |
| F | 0 | 60 | 60 | C schließt |
Angenommen ein Unternehmen C macht einen Gewinn von 40, wenn es produziert und ein Unternehmen F aufgrund von negativen Externalitäten 0. Wenn C nicht produziert, macht F einen Gewinn von 60. Die Tabelle oben verdeutlicht, dass unabhängig wer die Eigentumsrechte hat, rational geführte Verhandlungen zu einer pareto effizienten Allokation führen.
Für eine ausführlichere Beschreibung und weitere Szenarien, hier.
MC Fragen
