Karush-Kuhn-Tucker (KKT): Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Die Karush-Kuhn-Tucker Bedingungen sind ein notwendiges Optimalitätskriterium zur Bestimmung des Maximums/Minimums einer Zielfunktion mit Nebenbedingungen. Da…“) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 19: | Zeile 19: | ||
Das KKT Verfahren nutzt mehrere Bedingungen, um die Lösung für das Problem zu finden: <br> | Das KKT Verfahren nutzt mehrere Bedingungen, um die Lösung für das Problem zu finden: <br> | ||
FOC für alle zu maximierenden Variablen: <br> | FOC für alle zu maximierenden Variablen: <br> | ||
| − | <math> (i) \frac{\partial \mathcal{L}}{\partial x_1}\stackrel{!}{=}0 </math> <br> | + | <math> (i) \quad \frac{\partial \mathcal{L}}{\partial x_1}\stackrel{!}{=}0 </math> <br> |
| − | <math> (ii) \frac{\partial \mathcal{L}}{\partial x_2}\stackrel{!}{=}0 </math> <br> | + | <math> (ii) \quad \frac{\partial \mathcal{L}}{\partial x_2}\stackrel{!}{=}0 </math> <br> |
Die Ungleichungen selbst mit der Nichtnegativitätsbedingung der Lagrangemultiplikatoren: <br> | Die Ungleichungen selbst mit der Nichtnegativitätsbedingung der Lagrangemultiplikatoren: <br> | ||
| − | <math> (iii) E-p_1x_1-p_2x_2 \geq 0 </math>; <math> \lambda_1 \geq 0</math> <br> | + | <math> (iii) \quad E-p_1x_1-p_2x_2 \geq 0 </math>; <math> \lambda_1 \geq 0</math> <br> |
| − | <math> (iv) x_1 \geq 0 </math>; <math> \lambda_2 \geq 0</math><br> | + | <math> (iv) \quad x_1 \geq 0 </math>; <math> \lambda_2 \geq 0</math><br> |
| − | <math> (v) x_2 \geq 0 </math>; <math> \lambda_3 \geq 0</math><br> | + | <math> (v) \quad x_2 \geq 0 </math>; <math> \lambda_3 \geq 0</math><br> |
Den Komplementaritätsbedingung <br> | Den Komplementaritätsbedingung <br> | ||
| − | <math> (vi) \lambda_1(E-p_1x_1-p_2x_2)=0 </math> <br> | + | <math> (vi) \quad \lambda_1(E-p_1x_1-p_2x_2)=0 </math> <br> |
| − | <math> (vii) \lambda_2 x_2=0 </math> <br> | + | <math> (vii) \quad \lambda_2 x_2=0 </math> <br> |
| − | <math> (viii) \lambda_3 x_2=0 </math> <br> | + | <math> (viii) \quad \lambda_3 x_2=0 </math> <br> |
| + | |||
| + | Die Komplementaritätsbedingungen | ||
| − | |||
==Beispiel== | ==Beispiel== | ||
==MC Fragen== | ==MC Fragen== | ||
Version vom 3. April 2024, 11:14 Uhr
Die Karush-Kuhn-Tucker Bedingungen sind ein notwendiges Optimalitätskriterium zur Bestimmung des Maximums/Minimums einer Zielfunktion mit Nebenbedingungen. Das KKT Verfahren ist ein allgemeinerer Lösungsansatz verglichen mit dem Lagrange Verfahren, da auch Randlösungen betrachtet werden.
Randlösungen
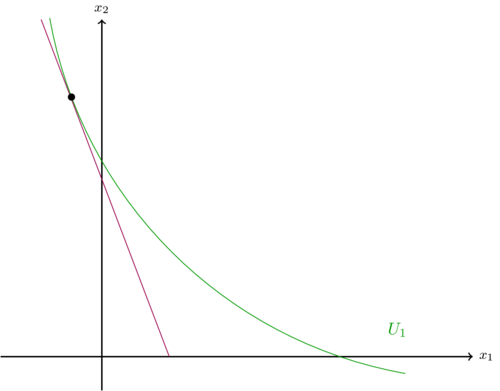
Das Lagrange Verfahren findet als Optimalitätsbedingung den Tangentialpunkt der Indifferenzkurve und der Budgetgeraden. In der Grafik unten wird das damit einhergehende Problem deutlich: Der Tangentialpunkt kann auch im negativen Bereich von einer der beiden Variablen sein. Dies liegt beispielweise an der Steigung der Budgetgeraden oder dem Verlauf der Indifferenzkurve. Im Falle der Nutzenmaximierung würde dies den Konsum einer negativen Menge bedeuten, was äußerst unrealistisch ist. Im grafischen Beispiel wäre das Ergebnis des Lagrange Verfahrens, dass der Konsument eine negative Menge von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
konsumieren sollte. Da dies nicht möglich ist, wäre es nutzenmaximal einen möglichen Punkt (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 \geq 0 }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2\geq 0 }
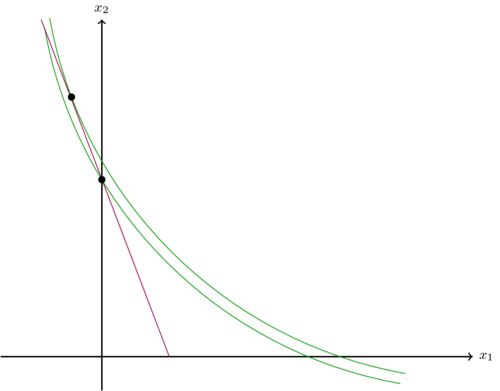
) zu konsumieren, der auf einer möglichst hohen Indifferenzkurve liegt. In dem grafischen Fall liegt der Punkt aufgrund der Annahmen über die Präferenzen auf der Budgetgeraden. Die höchste Indifferenzkurve die erreicht wird führt zu einem Konsumniveau von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1=0}
(zweite Abbildung). Dies ist eine Randlösung. Das KKT Verfahren findet das Punkt sofort, ohne dass die Lösung vom Lagrange Verfahren händisch korrigiert werden muss.
Nebenbedingungen
Das KKT Verfahren betrachtet mehrere Nebenbedingungen, um eine Lösung für das Maximierungsproblem zu finden. Diese sind häufig die Budgetbedingung und die Nichtnegativitätsbedingung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1x_1+p_2x_2 \leq E }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Leftrightarrow }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E-p_1x_1-p_2x_2 \geq 0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 \geq 0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 \geq 0 }
Die Nebenbedingungen werden jeweils mit einem Lagrangemultiplikator zu der Zielfunktion addiert:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{L} =U(x_1,x_2)+\lambda_1(E-p_1x_1-p_2x_2)+\lambda_2 x_1+\lambda_3x_2 }
Karush-Kuhn-Tucker-Bedingungen
Das KKT Verfahren nutzt mehrere Bedingungen, um die Lösung für das Problem zu finden:
FOC für alle zu maximierenden Variablen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (i) \quad \frac{\partial \mathcal{L}}{\partial x_1}\stackrel{!}{=}0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (ii) \quad \frac{\partial \mathcal{L}}{\partial x_2}\stackrel{!}{=}0 }
Die Ungleichungen selbst mit der Nichtnegativitätsbedingung der Lagrangemultiplikatoren:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (iii) \quad E-p_1x_1-p_2x_2 \geq 0 } ; Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_1 \geq 0}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (iv) \quad x_1 \geq 0 } ; Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_2 \geq 0}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (v) \quad x_2 \geq 0 } ; Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_3 \geq 0}
Den Komplementaritätsbedingung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (vi) \quad \lambda_1(E-p_1x_1-p_2x_2)=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (vii) \quad \lambda_2 x_2=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (viii) \quad \lambda_3 x_2=0 }
Die Komplementaritätsbedingungen