Moral Hazard und Anreize: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| (14 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Definition== | ==Definition== | ||
| − | Moral Hazard beschreibt | + | Moral Hazard beschreibt eine Inforamtionsasymmetrie nach Vertragsabschluss und stellt eine Art des [[Zusammenfassung Marktversagen|Marktversagens]] dar. Sie entsteht, da das Verhalten nach Vertragsabschluss nicht beobachtbar ist. Dies wird als ''hidden action'' bezeichnet und kann dazu führen, dass sich die Verhaltensmuster nach Vertragsabschluss verändern. Die Partei, die einen oder mehreren Agenten beauftragt, ein Ziel zu verfolgen, wird Prinzipal genannt. Die Partei, die von einem Prinzipal beauftragt wird, dessen Ziele zu verfolgen, wird Agent genannt. |
__TOC__ | __TOC__ | ||
==Moral Hazard== | ==Moral Hazard== | ||
| − | Moral Hazard beschreibt die Inforamtionsasymmetrie nach Vertragsabschluss. Unter der Annahme, dass vor Abschluss des Vertrages beide Seiten | + | Moral Hazard beschreibt die Inforamtionsasymmetrie nach Vertragsabschluss. Unter der Annahme, dass vor Abschluss des Vertrages beide Seiten dieselben Informationen haben, ändert sich diese Prämisse häufig nach Vertragsabschluss. <br> |
| − | ''Beispiel'': Ein Autofahrer ist sehr vorsichtig und ein Versicherer kann dieses Verhalten perfekt beobachten. Entsprechend seiner Unfallwahrscheinlichkeit bietet der Versicherer dem Autofahrer eine Autoversicherung an. Der Autofahrer schließt die Versicherung ab und zahlt monatlich | + | ''Beispiel'': Ein Autofahrer ist sehr vorsichtig und ein Versicherer kann dieses Verhalten perfekt beobachten. Entsprechend seiner Unfallwahrscheinlichkeit bietet der Versicherer dem Autofahrer eine Autoversicherung an. Der Autofahrer schließt die Versicherung ab und zahlt monatlich eine Versicherungsprämie, die zuvor vertraglich festgehalten wurde. Da der Autofahrer eine Versicherung hat, trägt er ein geringeres Risiko als ohne Versicherung. Im Falle eines Unfalls zahlt die Versicherung den Schaden. Der Autofahrer hat durch die Versicherung keinen Grund mehr vorsichtig zu fahren, was sein Fahrverhalten verändert. Durch die Versicherung verändert sich das Verhalten des Autofahrers, der Versicherer würde die Versicherung so nicht nochmal anbieten und es kommt zu einem [[Zusammenfassung Marktversagen|Marktversagen]]. Der Versicherer ist der Prinzipal und der Autofahrer der Agent. <br> |
| − | ''Ein weiteres Beispiel'': Auf dem Arbeitsmarkt werden Verträge nach Arbeitszeit geschlossen. Nach dem Abschluss des Vertrages bekommen Arbeitnehmer ihr Gehalt vom Arbeitgeber | + | ''Ein weiteres Beispiel'': Auf dem Arbeitsmarkt werden Verträge nach Arbeitszeit geschlossen. Nach dem Abschluss des Vertrages bekommen Arbeitnehmer ihr Gehalt vom Arbeitgeber ungeachtet dessen, wie produktiv sie in der vorgegebenen Zeit arbeiten. Dies verleitet Arbeitnehmer dazu möglichst geringe Anstrengungskosten zu haben. Der Arbeitnehmer ist der Agent und der Arbeitgeber der Prinzipal. <br> |
<br> | <br> | ||
Andere Beispiele sind: <br> | Andere Beispiele sind: <br> | ||
-Mit '''gemieteten Wohnungen''' wird anders umgegangen als mit eigenen Wohnungen ("Don't be gentle it's a rental") <br> | -Mit '''gemieteten Wohnungen''' wird anders umgegangen als mit eigenen Wohnungen ("Don't be gentle it's a rental") <br> | ||
| − | -'''Finanzkrise''': Fehlanreize an Eigenkapitalgeber von Banken mit hohem Fremd- zu Eigenkapitalanteil (bei etlichen Banken 30:1) insbesondere bei staatlicher Absicherung des Fremdkapitals (Einlagensicherung); Anreiz zu hoher Risikowahl; Anreiz wird an Bankmanager | + | -'''Finanzkrise''': Fehlanreize an Eigenkapitalgeber von Banken mit hohem Fremd- zu Eigenkapitalanteil (bei etlichen Banken 30:1) insbesondere bei staatlicher Absicherung des Fremdkapitals (Einlagensicherung); Anreiz zu hoher Risikowahl; Anreiz wird an Bankmanager weitergegeben. <br> |
| − | -'''Staatsschuldenkrise''': Bailout-Zusage für Staaten reduziert Sparanreize | + | -'''Staatsschuldenkrise''': Bailout-Zusage für Staaten reduziert Sparanreize |
==Theorie optimaler Verträge== | ==Theorie optimaler Verträge== | ||
| − | Optimal ausgestaltete Verträge sind der Versuch das veränderte Verhalten nach Vertragsabschluss zu verhindern. Ziel ist die | + | Optimal ausgestaltete Verträge sind der Versuch das veränderte Verhalten nach Vertragsabschluss zu verhindern. Ziel ist die Verträge derart auszugestalten, dass Anreize für Agenten entstehen die Verhaltensmuster für alle optimal anzupassen. Zur Erläuterung soll ein Beispiel aus dem Finanzwesen dienen: die Kreditrationierung, welche sowohl das Moral Hazard, als auch das [[Adverse Selektion und Signale|Adverse Selektion]]-Problem beinhaltet. <br> |
<br> | <br> | ||
'''Die Projekte''': <br> | '''Die Projekte''': <br> | ||
| − | In dem Beispiel stehen zwei Projekte zur Auswahl, die ein Unternehmer realisieren kann. Hierfür leiht er sich Geld von einer Bank in Höhe von I (I ist eine | + | In dem Beispiel stehen zwei Projekte zur Auswahl, die ein Unternehmer realisieren kann. Hierfür leiht er sich Geld von einer Bank in Höhe von I (I ist eine reelle Zahl). Beide Projekte (A und B) bringen mit einer jeweiligen Wahrscheinlichkeit einen unterschiedlichen Ertrag. Die Wahrscheinlichkeit, dass Projekt A erfolgreich ist wird <math> p_a </math> bezeichnet. Der Ertrag von Projekt A ist <math> X_a </math>, wobei X eine reelle Zahl ist (z.B. 10). Das gleiche gilt für Projekt B mit dem Index b. <br> |
<br> | <br> | ||
<math> \tilde{X}=\begin{cases} | <math> \tilde{X}=\begin{cases} | ||
| Zeile 30: | Zeile 30: | ||
\end{cases}</math> <br> | \end{cases}</math> <br> | ||
<br> | <br> | ||
| − | Es soll gelten <math> X_b>X_a </math>. Der Ertrag des Projektes B soll größer sein | + | Es soll gelten <math> X_b>X_a </math>. Der Ertrag des Projektes B soll größer sein als der von Unternehmen A. Außerdem soll <math> 1>p_a>p_b>0 </math> gelten. Projekt B hat also einen höheren Ertrag, der dafür aber unwahrscheinlicher als der von Projekt A ist. Insgesamt soll gelten <math> p_aX_a>p_bX_b>I </math>. Der erwartete Payoff von Projekt A ist größer als von Projekt B und beide sind größer als die Höhe des Kredits. Den Kredit muss der Unternehmer im Falle des Erfolgs samt Zinsen (<math> R=I(1+r)</math>) zurückzahlen. Stellt sich der Erfolg des Projektes nicht ein, kann er auch nichts zurückzahlen und der Gläubiger erhält kein Geld. <br> |
Der Nutzen des Unternehmers sei daher beschrieben durch <math> U(R,i)=P_i(X_i-R) </math> <br> | Der Nutzen des Unternehmers sei daher beschrieben durch <math> U(R,i)=P_i(X_i-R) </math> <br> | ||
: ''Beispiel: Projekt A hat eine Erfolgschance von 0,5 und bringt im Falle des Erfolgs einen Ertrag von 100. Der Kredit wurde in Höhe von 10 zu einem Zinssatz <math> r=10%</math> eingeräumt. <math> R </math> beträgt <math> R=10(1+0,1)=11 </math> Im Falle des Erfolgs muss der Unternehmer 11 zurückzahlen. Insgesamt bleibt ihm dementsprechend <math> X_a-R=100-11=89 </math>. Der Nutzen entspricht <math> U(R,p_a)=0,5(100-11)=44,5</math>'' <br> | : ''Beispiel: Projekt A hat eine Erfolgschance von 0,5 und bringt im Falle des Erfolgs einen Ertrag von 100. Der Kredit wurde in Höhe von 10 zu einem Zinssatz <math> r=10%</math> eingeräumt. <math> R </math> beträgt <math> R=10(1+0,1)=11 </math> Im Falle des Erfolgs muss der Unternehmer 11 zurückzahlen. Insgesamt bleibt ihm dementsprechend <math> X_a-R=100-11=89 </math>. Der Nutzen entspricht <math> U(R,p_a)=0,5(100-11)=44,5</math>'' <br> | ||
| − | Die Bank/der Gläubiger erhält im Erfolgsfall mit der Wahrscheinlichkeit <math> p_i</math> <math> R </math>, musste jedoch vorher I abgeben. Der erwartete Gewinn der Bank lautet <math> \pi(R,i)= | + | Die Bank/der Gläubiger erhält im Erfolgsfall mit der Wahrscheinlichkeit <math> p_i</math> <math> R </math>, musste jedoch vorher I abgeben. Der erwartete Gewinn der Bank lautet <math> \pi(R,i)=p_i(R-I) </math> Die Summe I gibt die Bank auf jeden Fall ab, <math> R </math> erhält sie nur im Erfolgsfall. <br> |
| − | : ''Im Beispiel bietet das Projekt A einen erwarteten Gewinn der Bank von 0,5, der sich wie folgt berechnen lässt <math> \pi(R,i)=0,5*11-10=0,5</math>'' <br> <br> | + | : ''Im Beispiel bietet das Projekt A einen erwarteten Gewinn der Bank von 0,5, der sich wie folgt berechnen lässt <math> \pi(R,i)=0,5*(11-10)=0,5</math>'' <br> <br> |
'''Der kritische Zinssatz''': <br> | '''Der kritische Zinssatz''': <br> | ||
| − | Unter der Annahme der symmetrischen Informationen würde jedes Projekt entsprechend seinem Risiko einen spezifischen Zinssatz bekommen, sodass <math> R_a \neq R_b</math>. Liegen jedoch | + | Unter der Annahme der symmetrischen Informationen würde jedes Projekt entsprechend seinem Risiko einen spezifischen Zinssatz bekommen, sodass <math> R_a \neq R_b</math>. Liegen jedoch asymmetrische Informationen vor, kann die Bank nicht kontrollieren welcher Kredit für welches Projekt verwendet wird. Es hängt von der Größe von <math> R </math> ab, welches Projekt von dem Unternehmer präferiert wird. Ist <math> R </math> sehr klein, wird Projekt A bevorzugt, da dieser einen höheren Ertrag bietet und relativ niedrige Zinskosten entstehen. Ist <math> R </math> jedoch sehr groß, würde vom Ertrag von Projekt A immer weniger für den Unternehmer übrigbleiben. Daher steigt er bei einem kritischen Zinssatz <math> \hat{R} </math> auf Projekt B um, das zwar unwahrscheinlicher ist, jedoch einen höheren Ertrag liefert. <br> |
Bei dem kritischen Zins <math> \hat{R} </math> ist der Unternehmer indifferent: <br> | Bei dem kritischen Zins <math> \hat{R} </math> ist der Unternehmer indifferent: <br> | ||
<math> p_a(X_a-\hat{R})=p_b(X_b-\hat{R}) </math> <br> | <math> p_a(X_a-\hat{R})=p_b(X_b-\hat{R}) </math> <br> | ||
| Zeile 50: | Zeile 50: | ||
\end{cases}</math> <br> | \end{cases}</math> <br> | ||
<br> | <br> | ||
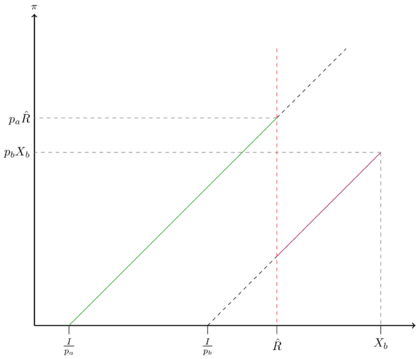
| − | Dies kann durch Umstellen auch grafisch dargestellt werden. Der Gewinn der Bank resultiert bis zu dem kritischen Zinssatz (Grenze in rot dargestellt) von den | + | Dies kann durch Umstellen auch grafisch dargestellt werden. Der Gewinn der Bank resultiert bis zu dem kritischen Zinssatz (Grenze in rot dargestellt) von den Zinserträgen bezahlt durch den Erfolg von Projekt A (in grün). Ab einem Zinssatz <math> \hat{R} </math> entscheidet sich der Unternehmer für Projekt B und der Gewinn wird durch die Gerade in lila beschrieben. Die Bank sollte einen Zinssatz <math> R=\hat{R} </math> (oder ganz leicht darunter) wählen, denn liegt der Zinssatz darüber ist der Gewinn geringer oder sogar negativ. Alle diejenige, die ein Kredit nachfragen, bekommen ihn nur noch zu <math> \hat{R} </math>, sodass der Payoff aller Kreditnachfrager <math> U(\hat{R},a)=p_a*(X_a-\hat{R})>0 </math> <br> |
| − | [[Datei:Kreditrationierung.png| | + | [[Datei:Kreditrationierung.png|420px|rahmenlos]] <br clear=all> |
<br> | <br> | ||
'''Die Rationierung''': <br> | '''Die Rationierung''': <br> | ||
| Zeile 62: | Zeile 62: | ||
|type="()"} | |type="()"} | ||
+ Ein Student mit dem Spitznamen scaredy schließt eine Versicherung gegen alle möglichen Gründe ab, da er besonders ängstlich ist. | + Ein Student mit dem Spitznamen scaredy schließt eine Versicherung gegen alle möglichen Gründe ab, da er besonders ängstlich ist. | ||
| − | - Eine | + | - Eine Autovermietung namens AmeriCar bietet eine Vollkasko mit 0€ Selbstbeteiligung, deshalb fahren die Mieterinnen und Mieter der Autos unvorsichtiger. |
- Im Unternehmen Careless werden Manager direkt am Gewinn beteiligt und versuchen daher den Gewinn auf Kosten des zukünftigen Gewinns zu steigern | - Im Unternehmen Careless werden Manager direkt am Gewinn beteiligt und versuchen daher den Gewinn auf Kosten des zukünftigen Gewinns zu steigern | ||
- Der Besitzer des Restaurants OnFire, der eine Feuerversicherung besitzt, zündet sein Restaurant an. | - Der Besitzer des Restaurants OnFire, der eine Feuerversicherung besitzt, zündet sein Restaurant an. | ||
Aktuelle Version vom 2. Oktober 2024, 16:58 Uhr
Definition
Moral Hazard beschreibt eine Inforamtionsasymmetrie nach Vertragsabschluss und stellt eine Art des Marktversagens dar. Sie entsteht, da das Verhalten nach Vertragsabschluss nicht beobachtbar ist. Dies wird als hidden action bezeichnet und kann dazu führen, dass sich die Verhaltensmuster nach Vertragsabschluss verändern. Die Partei, die einen oder mehreren Agenten beauftragt, ein Ziel zu verfolgen, wird Prinzipal genannt. Die Partei, die von einem Prinzipal beauftragt wird, dessen Ziele zu verfolgen, wird Agent genannt.
Moral Hazard
Moral Hazard beschreibt die Inforamtionsasymmetrie nach Vertragsabschluss. Unter der Annahme, dass vor Abschluss des Vertrages beide Seiten dieselben Informationen haben, ändert sich diese Prämisse häufig nach Vertragsabschluss.
Beispiel: Ein Autofahrer ist sehr vorsichtig und ein Versicherer kann dieses Verhalten perfekt beobachten. Entsprechend seiner Unfallwahrscheinlichkeit bietet der Versicherer dem Autofahrer eine Autoversicherung an. Der Autofahrer schließt die Versicherung ab und zahlt monatlich eine Versicherungsprämie, die zuvor vertraglich festgehalten wurde. Da der Autofahrer eine Versicherung hat, trägt er ein geringeres Risiko als ohne Versicherung. Im Falle eines Unfalls zahlt die Versicherung den Schaden. Der Autofahrer hat durch die Versicherung keinen Grund mehr vorsichtig zu fahren, was sein Fahrverhalten verändert. Durch die Versicherung verändert sich das Verhalten des Autofahrers, der Versicherer würde die Versicherung so nicht nochmal anbieten und es kommt zu einem Marktversagen. Der Versicherer ist der Prinzipal und der Autofahrer der Agent.
Ein weiteres Beispiel: Auf dem Arbeitsmarkt werden Verträge nach Arbeitszeit geschlossen. Nach dem Abschluss des Vertrages bekommen Arbeitnehmer ihr Gehalt vom Arbeitgeber ungeachtet dessen, wie produktiv sie in der vorgegebenen Zeit arbeiten. Dies verleitet Arbeitnehmer dazu möglichst geringe Anstrengungskosten zu haben. Der Arbeitnehmer ist der Agent und der Arbeitgeber der Prinzipal.
Andere Beispiele sind:
-Mit gemieteten Wohnungen wird anders umgegangen als mit eigenen Wohnungen ("Don't be gentle it's a rental")
-Finanzkrise: Fehlanreize an Eigenkapitalgeber von Banken mit hohem Fremd- zu Eigenkapitalanteil (bei etlichen Banken 30:1) insbesondere bei staatlicher Absicherung des Fremdkapitals (Einlagensicherung); Anreiz zu hoher Risikowahl; Anreiz wird an Bankmanager weitergegeben.
-Staatsschuldenkrise: Bailout-Zusage für Staaten reduziert Sparanreize
Theorie optimaler Verträge
Optimal ausgestaltete Verträge sind der Versuch das veränderte Verhalten nach Vertragsabschluss zu verhindern. Ziel ist die Verträge derart auszugestalten, dass Anreize für Agenten entstehen die Verhaltensmuster für alle optimal anzupassen. Zur Erläuterung soll ein Beispiel aus dem Finanzwesen dienen: die Kreditrationierung, welche sowohl das Moral Hazard, als auch das Adverse Selektion-Problem beinhaltet.
Die Projekte:
In dem Beispiel stehen zwei Projekte zur Auswahl, die ein Unternehmer realisieren kann. Hierfür leiht er sich Geld von einer Bank in Höhe von I (I ist eine reelle Zahl). Beide Projekte (A und B) bringen mit einer jeweiligen Wahrscheinlichkeit einen unterschiedlichen Ertrag. Die Wahrscheinlichkeit, dass Projekt A erfolgreich ist wird Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_a }
bezeichnet. Der Ertrag von Projekt A ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_a }
, wobei X eine reelle Zahl ist (z.B. 10). Das gleiche gilt für Projekt B mit dem Index b.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{X}=\begin{cases} X_a, & \text{mit Wahrscheinlichkeit } p_a; \\ 0, & \text{mit Wahrscheinlichkeit } 1-p_a; \end{cases}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tilde{X}=\begin{cases} X_b, & \text{mit Wahrscheinlichkeit } \, p_b; \\ 0, & \text{mit Wahrscheinlichkeit } \, 1-p_b; \end{cases}}
Es soll gelten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_b>X_a }
. Der Ertrag des Projektes B soll größer sein als der von Unternehmen A. Außerdem soll Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1>p_a>p_b>0 }
gelten. Projekt B hat also einen höheren Ertrag, der dafür aber unwahrscheinlicher als der von Projekt A ist. Insgesamt soll gelten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_aX_a>p_bX_b>I }
. Der erwartete Payoff von Projekt A ist größer als von Projekt B und beide sind größer als die Höhe des Kredits. Den Kredit muss der Unternehmer im Falle des Erfolgs samt Zinsen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R=I(1+r)}
) zurückzahlen. Stellt sich der Erfolg des Projektes nicht ein, kann er auch nichts zurückzahlen und der Gläubiger erhält kein Geld.
Der Nutzen des Unternehmers sei daher beschrieben durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(R,i)=P_i(X_i-R) }
- Beispiel: Projekt A hat eine Erfolgschance von 0,5 und bringt im Falle des Erfolgs einen Ertrag von 100. Der Kredit wurde in Höhe von 10 zu einem Zinssatz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r=10%}
eingeräumt. beträgt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R=10(1+0,1)=11 }
Im Falle des Erfolgs muss der Unternehmer 11 zurückzahlen. Insgesamt bleibt ihm dementsprechend Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_a-R=100-11=89 }
. Der Nutzen entspricht Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(R,p_a)=0,5(100-11)=44,5}
Die Bank/der Gläubiger erhält im Erfolgsfall mit der Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_i}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R }
, musste jedoch vorher I abgeben. Der erwartete Gewinn der Bank lautet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi(R,i)=p_i(R-I) }
Die Summe I gibt die Bank auf jeden Fall ab, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R }
erhält sie nur im Erfolgsfall.
- Im Beispiel bietet das Projekt A einen erwarteten Gewinn der Bank von 0,5, der sich wie folgt berechnen lässt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi(R,i)=0,5*(11-10)=0,5}
Der kritische Zinssatz:
Unter der Annahme der symmetrischen Informationen würde jedes Projekt entsprechend seinem Risiko einen spezifischen Zinssatz bekommen, sodass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R_a \neq R_b}
. Liegen jedoch asymmetrische Informationen vor, kann die Bank nicht kontrollieren welcher Kredit für welches Projekt verwendet wird. Es hängt von der Größe von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R }
ab, welches Projekt von dem Unternehmer präferiert wird. Ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R }
sehr klein, wird Projekt A bevorzugt, da dieser einen höheren Ertrag bietet und relativ niedrige Zinskosten entstehen. Ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R }
jedoch sehr groß, würde vom Ertrag von Projekt A immer weniger für den Unternehmer übrigbleiben. Daher steigt er bei einem kritischen Zinssatz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{R} }
auf Projekt B um, das zwar unwahrscheinlicher ist, jedoch einen höheren Ertrag liefert.
Bei dem kritischen Zins Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{R} }
ist der Unternehmer indifferent:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_a(X_a-\hat{R})=p_b(X_b-\hat{R}) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{R}=\frac{p_aX_a-p_bX_b}{p_a-p_b} }
Ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R \leq \hat{R}}
wird Projekt A gewählt und ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R>\hat{R}}
wird Projekt B gewählt.
Die Gewinnfunktion der Bank:
Aus dem Ergebnis oben resultiert eine Gewinnfunktion für die Bank:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi^*(R)=\begin{cases} P_aR-I, & \text{wenn } 0\leq R \leq \hat{R}; \\ P_bR-I, & \text{wenn } \hat{R} < R < X-b; \end{cases}}
Dies kann durch Umstellen auch grafisch dargestellt werden. Der Gewinn der Bank resultiert bis zu dem kritischen Zinssatz (Grenze in rot dargestellt) von den Zinserträgen bezahlt durch den Erfolg von Projekt A (in grün). Ab einem Zinssatz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{R} }
entscheidet sich der Unternehmer für Projekt B und der Gewinn wird durch die Gerade in lila beschrieben. Die Bank sollte einen Zinssatz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R=\hat{R} }
(oder ganz leicht darunter) wählen, denn liegt der Zinssatz darüber ist der Gewinn geringer oder sogar negativ. Alle diejenige, die ein Kredit nachfragen, bekommen ihn nur noch zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \hat{R} }
, sodass der Payoff aller Kreditnachfrager Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(\hat{R},a)=p_a*(X_a-\hat{R})>0 }
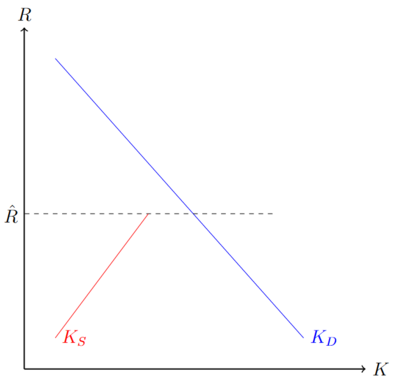
Die Rationierung:
Alle Kreditnehmer fragen einen Kredit zu den Konditionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (I,\hat{R})}
nach. Ist aber das Kreditangebot bei diesem Zinssatz geringer als die Nachfrage, kommt es zu einer nicht-preislichen Kreditrationierung. Die folgende Abbildung veranschaulicht die Situation, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_D }
die Kreditnachfrage und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_S }
das Kreditangebot widerspiegeln:
MC Aufgaben
