Erwartungswert und Varianz: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 4: | Zeile 4: | ||
==Erwartungswert (Durchschnitt/Mittelwert)== | ==Erwartungswert (Durchschnitt/Mittelwert)== | ||
| − | Der Erwartungswert ist eine Maßzahl und beschreibt welche Beobachtung im Durchschnitt auftritt. | + | Der Erwartungswert ist eine Maßzahl und beschreibt welche Beobachtung im Durchschnitt auftritt. Es gilt hierbei zwischen dem Mittelwert einer Beobachtung und dem Durchschnitt der "Population" zu unterscheiden. Um den Unterschied zu verdeutlichen sollen Münzwürfe dienen. Es ist möglich den Mittelwert von beispielsweise 10 Münzwürfen auszurechnen. Dann lautet die Berechnung des realisierten Mittelwertes: μ<math>= 1/10(x_1 + x_2 + \ldots + x_{10}) </math>. <math> x_1 </math> ist hier die Ausprägung des ersten Münzwurfs (Kopf oder Zahl). Der Durchschnitt der "Bevölkerung" lässt sich simulieren, in dem die Anzahl der Münzwürfe immer weiter vergrößert wird und letztlich gegen unendlich strebt. An dieser Stelle spielen Wahrscheinlichkeiten eine Rolle. In unserem Beispiel soll von einer fairen Münze ausgegangen werden, sodass beide Seiten gleich wahrscheinlich sind. Wird dementsprechend eine Münze geworfen fällt mit Wahrscheinlichkeit 0,5 Kopf und mit der Wahrscheinlichkeit 0,5 Zahl. Wenn 10 Mal Münzen geworfen werden, so kann erwartet werden, dass bei 5 der Würfen Kopf und bei 5 der Würfen Zahl fällt. Ein weiteres Beispiel ist ein fairer Würfel, bei dem jede Seite mit der Wahrscheinlichkeit 1/6 fällt. Für den Erwartungswert eines Wurfes lässt sich die Augenzahl mit der Wahrscheinlichkeit multiplizieren: <math> E[X]=1/6*1+1/6*2+...1/6*6 </math>, wobei <math> X </math> die Augenzahl ist. Für einen allgemeinen Fall lässt sich die Formel wie folgt beschreiben: <br> |
| − | + | <math> E[X]=\sum_{i=1}^{n}x_i \cdot p_i </math> | |
| − | + | <math> p_i </math> ist die Wahrscheinlichkeit für eine bestimmte Ausprägung, <math> x_i </math> ist die Ausprägung selbst und <math> n </math> ist die Anzahl der möglichen Ausprägungen. Beispiel Augenzahl 2: <math> x_2=2 </math>, <math> p_2=1/6 </math> und <math> n=6 </math> <br> | |
| − | <math> E[X]=\sum_{i=1}^{n}x_i \cdot p_i </math> <br> | + | ''Beispiel:'' In einem Casino werden zwei Münzen geworfen. Beide Münzen sind identisch und auf einer Seite steht jeweils "1" und auf der anderen Seite "2". Besucher des Casinos können auf die Summer der Münzseiten wetten, die nach oben zeigen. Um eine bessere Wette platzieren zu können, berechnet Max den Erwartungswert aus. Die Summe der Münzen beträgt 2, wenn beide Münzen die 1 aufweisen. Die Wahrscheinlichkeit hierfür beträgt <math> 1/2 \cdot 1/2=1/4 </math>. Analog verhält es sich für die Summe 4. Die Summe drei liegt, wenn einer der Münzen eine 1 und die andere eine 2 aufweist. Es gibt also zwei Events, bei der die Summe 3 eintritt. Beide Events treten mit der Wahrscheinlichkeit <math> 1/4 </math> auf. Daher beträgt die Wahrscheinlichkeit für 3 als Summe <math> 1/4+1/4=1/2 </math>. Die erwartete Summe baträgt somit <math> 1/4 \cdot 2+1/2 \cdot 3 + 1/4 \cdot 4=3 </math> <br> <br> |
| − | Die | + | In der Mikroökonomie wird vor allem der Durchschnitt der Population betrachtet. Im Fall der Entscheidung unter [[Risiko und Risikoeinstellung|Risiko]], werden Wahrscheinlichkeiten zur Berechnung eines Erwartungswertes herangezogen. |
==Varianz== | ==Varianz== | ||
Version vom 4. Oktober 2024, 16:20 Uhr
Statistische Maßzahlen wie der Erwartungswert und die Varianz haben auch in der Mikroökonomie eine nicht unwichtige Bedeutung. Sie spielen zum Beispiel bei Entscheidungen unter Risiko eine Rolle.
Erwartungswert (Durchschnitt/Mittelwert)
Der Erwartungswert ist eine Maßzahl und beschreibt welche Beobachtung im Durchschnitt auftritt. Es gilt hierbei zwischen dem Mittelwert einer Beobachtung und dem Durchschnitt der "Population" zu unterscheiden. Um den Unterschied zu verdeutlichen sollen Münzwürfe dienen. Es ist möglich den Mittelwert von beispielsweise 10 Münzwürfen auszurechnen. Dann lautet die Berechnung des realisierten Mittelwertes: μFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle = 1/10(x_1 + x_2 + \ldots + x_{10}) }
. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
ist hier die Ausprägung des ersten Münzwurfs (Kopf oder Zahl). Der Durchschnitt der "Bevölkerung" lässt sich simulieren, in dem die Anzahl der Münzwürfe immer weiter vergrößert wird und letztlich gegen unendlich strebt. An dieser Stelle spielen Wahrscheinlichkeiten eine Rolle. In unserem Beispiel soll von einer fairen Münze ausgegangen werden, sodass beide Seiten gleich wahrscheinlich sind. Wird dementsprechend eine Münze geworfen fällt mit Wahrscheinlichkeit 0,5 Kopf und mit der Wahrscheinlichkeit 0,5 Zahl. Wenn 10 Mal Münzen geworfen werden, so kann erwartet werden, dass bei 5 der Würfen Kopf und bei 5 der Würfen Zahl fällt. Ein weiteres Beispiel ist ein fairer Würfel, bei dem jede Seite mit der Wahrscheinlichkeit 1/6 fällt. Für den Erwartungswert eines Wurfes lässt sich die Augenzahl mit der Wahrscheinlichkeit multiplizieren: , wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X }
die Augenzahl ist. Für einen allgemeinen Fall lässt sich die Formel wie folgt beschreiben:
![{\displaystyle E[X]=1/6*1+1/6*2+...1/6*6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc5b86a46ef29efdaa90d2ee54c48dac49f39998)
![{\displaystyle E[X]=\sum _{i=1}^{n}x_{i}\cdot p_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9880293cbe99e44cde58103884bd7a5dbd0894c8)
ist die Wahrscheinlichkeit für eine bestimmte Ausprägung, ist die Ausprägung selbst und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n }
ist die Anzahl der möglichen Ausprägungen. Beispiel Augenzahl 2: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2=2 }
, und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=6 }
Beispiel: In einem Casino werden zwei Münzen geworfen. Beide Münzen sind identisch und auf einer Seite steht jeweils "1" und auf der anderen Seite "2". Besucher des Casinos können auf die Summer der Münzseiten wetten, die nach oben zeigen. Um eine bessere Wette platzieren zu können, berechnet Max den Erwartungswert aus. Die Summe der Münzen beträgt 2, wenn beide Münzen die 1 aufweisen. Die Wahrscheinlichkeit hierfür beträgt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1/2 \cdot 1/2=1/4 }
. Analog verhält es sich für die Summe 4. Die Summe drei liegt, wenn einer der Münzen eine 1 und die andere eine 2 aufweist. Es gibt also zwei Events, bei der die Summe 3 eintritt. Beide Events treten mit der Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1/4 }
auf. Daher beträgt die Wahrscheinlichkeit für 3 als Summe . Die erwartete Summe baträgt somit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1/4 \cdot 2+1/2 \cdot 3 + 1/4 \cdot 4=3 }
In der Mikroökonomie wird vor allem der Durchschnitt der Population betrachtet. Im Fall der Entscheidung unter Risiko, werden Wahrscheinlichkeiten zur Berechnung eines Erwartungswertes herangezogen.
Varianz
Die Varianz (auch "Mittlere quadratische Streuung") ist eine Maßzahl die angibt, wie häufig, wie sehr Beobachtungen um den Mittelwert streuen. Um zu erklären was damit gemeint ist sollen die folgenden Grafiken als Beispiel dienen. Sowohl im roten, als auch im grünen Fall werden 150 Ausprägungen beobachtet. In beiden ist der Mittelwert die 4, was sich daran erkennen lässt, das der Balken bei 4 in beiden Balkendiagrammen am höchsten ist und die Werte alle nahe an der 4 liegen. Dies lässt sich jedoch auch an den Grafiken mit den Punkten erkenne: Die 4 scheint am nächsten an allen Punkten dran zu sein. Dennoch ist auch erkennbar, dass die Punkte im grünen Fall deutlich näher an der 4 liegen, als im roten Fall, bei dem die Punkte deutlich gestreuter erscheinen. Eben diese Streuung lässt sich in der Varianz berechnen. Hierfür wird über die Differenz zwischen dem Mittelwert und der einzelnen Ausprägung aufsummiert, nachdem sie quadriert wurde. Um die Varianz als Maßzahl besser mit anderen Varianzen zu vergleichen, werden die Summen durch die Anzahl der Beobachtungen geteilt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d^2=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2 }
, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar{x} }
der Mittelwert ist
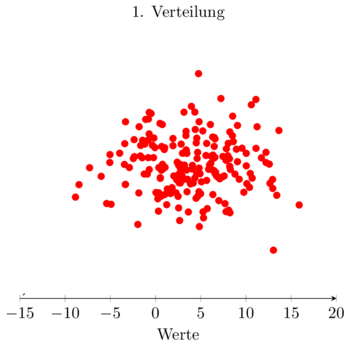
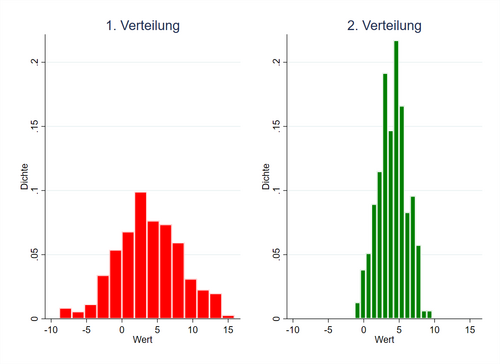
In dem grafischen Beispiel wird ersichtlich, dass die Werte alle nahe an der vier liegen und die vier auch am wahrscheinlichsten ist. Es kann aber auch unter anderem Fälle geben, bei denen alle Ausprägungen gleich wahrscheinlich sind, bei einer Verteilung jedoch weitaus extremere Beobachtungen auftreten. Auch hier kann der Erwartungswert in beiden Verteilungen identisch und die Varianz unterschiedlich sein.
Angenommen die Dichtefunktionen sind die Wahrscheinlichkeiten von jeweils einer Lotterie. Wenn ein Konsument dazu aufgefordert wird für beide Lotterien eine Zahl zu nennen und abhängig von dem Ergebnis erhält er eine Auszahlung, dann sollte er in beiden Fällen die 4 auswählen. Wird er zusätzlich aufgefordert zwischen einer der beiden Lotterien zu wählen, dann sollte er die grüne Lotterie wählen, da dort die 4 wahrscheinlicher, bzw. die Varianz kleiner ist.
MC Fragen
