Präferenzen und Indifferenzkurven: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ __TOC__ ==Präferenzen== ==Indifferenzkurven== ==Indifferenzkurven der Güterarten== ==MC Fragen==“) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | + | Individuen zeigen in ihrem Konsumverhalten Präferenzen. Diese Präferenzen spiegeln sich in ihrem Nutzenniveau wieder, das sich bei einer gleichen Güterkombination und unterschiedlichen Konsumentenpräferenzen unterscheiden kann. | |
__TOC__ | __TOC__ | ||
| − | ==Präferenzen== | + | ==Präferenzen und Nutzenfunktion== |
| + | Eine jede Marktteilnehmerin und ein jeder Marktteilnehmer verfügen über Präferenzen. Ein Mensch der Vegetarier ist, kauft zum Beispiel kein Fleisch. Für ein Filmabend gibt es Menschen, die lediglich salzige Snacks konsumieren, oder auch welche, für die nur süße Snacks in Frage kommen. Es gibt jedoch auch sicherlich Menschen, denen es egal ist welche Art der Snacks zu sich nehmen. <br> | ||
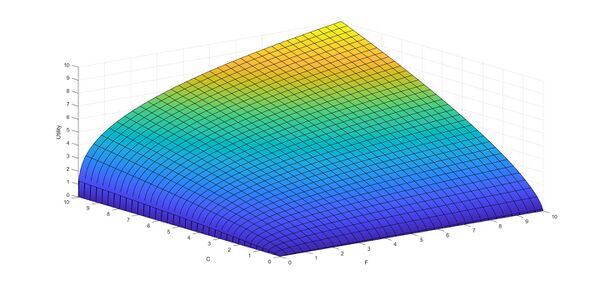
| + | Um all diese Präferenzen abbilden zu können werden Nutzenfunktionen modelliert. Hierfür wird dich der [[Ordinalen Nutzentheorie]] und nicht der [[kardinalen Nutzentheorie]] bedient. Je nach Präferenzen sehen die Nutzenfunktionen unterschiedlich aus. In jedem Fall sind sie jedoch abhängig von jedem zu betrachteten Gut und der Anzahl der davon konsumierten Einheiten <math display="inline"> U(x_{1}, x_{2}, x_{3}, ..., x_{n}) </math>. Der Einfachheit halber, und um die Nutzenfunktion grafisch darstellen zu können, beschränken wir uns auf den zwei-Güter-Fall. <math display="inline"> U(x_{1}, x_{2}) </math>. Als Beipsiel sollen uns die beiden Güter C und F dienen, die mit folgender Nutzenfunktion abgebildet werden sollen: <br> | ||
| + | <math display="inline"> U(F,C)=F^{1/3}*C^{2/3} </math> <br> | ||
| + | Die Nutzenfunktion kann als normale bivariate Funktion gelesen werden. Anders als im univariaten Fall ist die Funktion von zwei Variablen abhängig. <br> | ||
| + | [[Datei:Nutzenfunktion.jpg|600px|rahmenlos]] | ||
==Indifferenzkurven== | ==Indifferenzkurven== | ||
Version vom 25. Mai 2023, 10:05 Uhr
Individuen zeigen in ihrem Konsumverhalten Präferenzen. Diese Präferenzen spiegeln sich in ihrem Nutzenniveau wieder, das sich bei einer gleichen Güterkombination und unterschiedlichen Konsumentenpräferenzen unterscheiden kann.
Präferenzen und Nutzenfunktion
Eine jede Marktteilnehmerin und ein jeder Marktteilnehmer verfügen über Präferenzen. Ein Mensch der Vegetarier ist, kauft zum Beispiel kein Fleisch. Für ein Filmabend gibt es Menschen, die lediglich salzige Snacks konsumieren, oder auch welche, für die nur süße Snacks in Frage kommen. Es gibt jedoch auch sicherlich Menschen, denen es egal ist welche Art der Snacks zu sich nehmen.
Um all diese Präferenzen abbilden zu können werden Nutzenfunktionen modelliert. Hierfür wird dich der Ordinalen Nutzentheorie und nicht der kardinalen Nutzentheorie bedient. Je nach Präferenzen sehen die Nutzenfunktionen unterschiedlich aus. In jedem Fall sind sie jedoch abhängig von jedem zu betrachteten Gut und der Anzahl der davon konsumierten Einheiten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(x_{1}, x_{2}, x_{3}, ..., x_{n}) }
. Der Einfachheit halber, und um die Nutzenfunktion grafisch darstellen zu können, beschränken wir uns auf den zwei-Güter-Fall. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(x_{1}, x_{2}) }
. Als Beipsiel sollen uns die beiden Güter C und F dienen, die mit folgender Nutzenfunktion abgebildet werden sollen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(F,C)=F^{1/3}*C^{2/3} }
Die Nutzenfunktion kann als normale bivariate Funktion gelesen werden. Anders als im univariaten Fall ist die Funktion von zwei Variablen abhängig.