Ordinale und Kardinale Nutzentheorie: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 65: | Zeile 65: | ||
| 0 | | 0 | ||
|} | |} | ||
| − | Angenommen ein Konsument kann sich zwischen drei Optionen entscheiden <math> A_{1} </math>, <math> A_{2} </math> oder <math> A_{3} </math>. Die Drei Optionen bingen je nach S_{i} i \in {1,2,3,4} einen | + | Angenommen ein Konsument kann sich zwischen drei Optionen entscheiden <math> A_{1} </math>, <math> A_{2} </math> oder <math> A_{3} </math>. Die Drei Optionen bingen je nach <math> S_{i} </math>, <math> i \in </math> {1,2,3,4}, einen unterschiedlichen Nutzen. Was kann auf Basis der in der Tabelle stehenden Nutzenwerten gesagt werden? |
|type="()"} | |type="()"} | ||
| − | + Die Option <math> A_{2} wird nie gegenüber den anderen beiden Optionen präferiert. | + | + Die Option <math> A_{2} </math> wird nie gegenüber den anderen beiden Optionen präferiert. |
- Die Option <math> A_{1} </math> wird immer gegenüber den beiden anderen Optionen präferiert. | - Die Option <math> A_{1} </math> wird immer gegenüber den beiden anderen Optionen präferiert. | ||
| − | - Die Option <math> A_{3} wird immer gegenüber Optionen <math> A_{1} </math> präferiert. | + | - Die Option <math> A_{3} </math> wird immer gegenüber Optionen <math> A_{1} </math> präferiert. |
- Es lässt sich aufgrund der ordinalen Nutzenntheorie keine Aussage treffen. | - Es lässt sich aufgrund der ordinalen Nutzenntheorie keine Aussage treffen. | ||
</quiz> | </quiz> | ||
Version vom 1. Juni 2023, 14:43 Uhr
In der Nutzentheorie wird häufig zwischen der Kardinalen und der Ordinalen Nutzenthorie unterschieden. Während die Kardinale Nutzentheorie numerische Werte verwendet um zu beschreiben wie viel besser oder schlechter ein gewisser Nutzen ist nutzt die ordinale Nutzentheorie die numerischen Werte um zu beschreiben welcher welcher Nutzen größer oder kleiner ist.
Ordinale Nutzentheorie
In der ordinalen Nutzentheorie wird verglichen welcher Nutzen größer oder kleiner ist. Bei einer Nutzenfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(x,y)=x+y }
bieten ein x und ein y einen Nutzen von 2. Zwei x und zwei y bieten einen Nutzen von 4. Der Nutzen von dem ersten Bündel bringt einen geringeren Nutzen als das zweite Bündel. Ein Konsument präferiert dementsprechend das erste Bündel gegenüber dem zweiten Bündel. Eine Beschreibung als wie viel besser er das erste Bündel gegenüber dem zweiten Bündel bewertet, lässt sich mit der Ordinalen Nutzentheorie nicht sagen. Bei Indifferenzkurven kann somit lediglich gesagt werden, dass alle Güterkombinationen auf der Indifferenzkurve Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{2} }
allen möglichen Kombinationen auf der Indifferenzkurve Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{1} }
präferiert werden, falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{1} < U_{2} < U_{3} }
gilt.
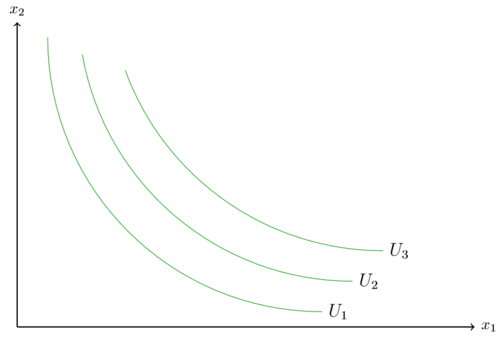
Ordinale Nutzenfunktionen bringen alle Warenkörbe vom beliebtesten zum unbeliebtesten Warenkorb in eine Rangfolge ("Ordnung").
Es ist jedoch nicht möglich zwischen dem Nutzen verschiedener Konsumenten zu vergleichen. Erfährt Konsument 1 von einem Gut einen Nutzen von 5 und Konsument 2 von dem selben Gut einen Nutzen von 6, ist es nicht möglich zu sagen welcher Konsument Nutzenmaximal das Gut erhalten sollte. Der Nutzen von Konsument 1 kann in kein Verhältnis zu dem Nutzen von Kosument 2 gestellt werden.
Oridinale Nutzentorie und monotone Präferenzen
Das es in der ordinalen Nutzentheorie darum geht Präferenzen durch eine Rangordnung darzustellen, ist es auch möglich etwaige Nutzenfunktionen monoton zu tranformieren soweit die Rangordnung nicht verändert wird.
Beispiel: Gegeben sei die Nutzenfunktion von oben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(x,y)=x+y }
. Eine monotone Transformation könnte wie folgt aussehen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U'(x,y)=2*(x+y)=2x+2y }
. Ein Bündel von (x,y)=(2,2) wird auch nach der Transformation gegenüber einem Bündel (x,y)=(1,1) präferiert. Das (x,y)=(1,1) Bündel bringt einmal einen Nutzen vn 2 und einmal einen Nutzen von 4. Das (x,y)=(2,2) Bündel bringt einen Nutzen von 4 beziehungsweise 8. 2 < 4 und 4 < 8. Dieses Beispiel zeigt, dass das numerische Nutzenniveau im Grunde lediglich eine Kennzahl zur Einordung im Vergleich mit einem anderen Nutzen dient. Die Präferenzen selbst werden mit einer monoton tranformierten Nutzenfunktion unverändert dargestellt.
Kardinale Nutzentheorie
Die kardinale Nutzentheorie wurde vorrangig in der Vergangenheit verwendet. In der kardinalen Nutzentheorie wird dem numerischen Nutzenniveau ein Wert beigemessen. Demnach ist ein Nutzen von 2 nicht nur größer als ein Nutzen von 1, sondern auch doppelt so gut.
In der Abbildung von oben bedeutet dies, dass alle Güterkombinationen auf der Indifferenzkurve Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{1} }
als halb so gut angesehen werden als alle Güterkombinationen auf der Indifferenzkurve Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{2} }
(angenommen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{2} }
ist doppelt so groß wie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{1} }
).
MC Aufgaben