Substitutionseffekt: Unterschied zwischen den Versionen
| Zeile 20: | Zeile 20: | ||
== Quantitatives Beispiel bei normalen Gütern == | == Quantitatives Beispiel bei normalen Gütern == | ||
| − | Die ursprünglichen Preise seien <math display="inline"> p_{x}^{0} = 10</math> und <math display="inline"> | + | ''Aufgabenstellung:'' Die ursprünglichen Preise seien <math display="inline"> p_{x}^{0} = 10</math> und <math display="inline"> p_{y} = 20</math>, das nominale Einkommen betrage <math display="inline"> E^{0} = 200</math>. Wir unterstellen die Nutzenfunktion <math display="inline"> u = x^{0,6}y^{0,4} </math>. Die jeweiligen Nachfragemengen <math display="inline"> x^{0} = 12</math> und <math display="inline"> y^{0} = 4 </math> können über den Lagrange-Ansatz berechnet werden. |
| + | |||
| + | ''Berchnung des Substitutionseffektes:'' Kompensiertes Einkommen (Einkommen, das es erlaubt, das alte Güterbündel zu neuen | ||
| + | Preisen zu erwerben): <math display="inline"> E^{1} = p_{x}^1x(p_{x}^0,p_{y},E^0) + p_{y}y(p_{x}^{0}) = 320</math> | ||
== Beispiel bei inferioren Gütern == | == Beispiel bei inferioren Gütern == | ||
Version vom 6. Mai 2022, 16:26 Uhr
Definition
Der Substitutionseffekt (SE) beschreibt den Effekt einer Preisänderung auf die relativen Preise zweier Güter. Dieser Effekt macht das relativ teurere Gut relativ unattraktiver.
Grafisches Beispiel bei normalen Gütern
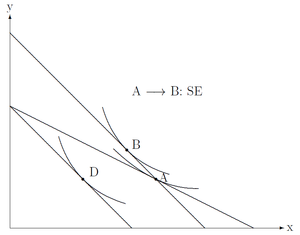
Betrachten wir nun den Substitutionseffekt bei einer Preisänderung:
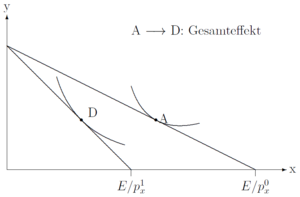
Das Ausgangsoptimum sei im Punkt A gegeben. Eine Preiserhöhung von Gut X führt dann zu dem neuen optimalen Konsumbündel D. Dies beschreibt den Gesamteffekt:
Die Grundidee ist, dass sich der Gesamteffekt aus zwei Teileffekten ergibt: Substitutionseffekt und Einkommenseffekt
Der SE ist stets eindeutig: wenn der Preis des Gutes X steigt, sinkt die Nachfrage nach X (und umgekehrt).
Quantitatives Beispiel bei normalen Gütern
Aufgabenstellung: Die ursprünglichen Preise seien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{x}^{0} = 10} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{y} = 20} , das nominale Einkommen betrage Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle E^{0} = 200} . Wir unterstellen die Nutzenfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle u = x^{0,6}y^{0,4} } . Die jeweiligen Nachfragemengen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x^{0} = 12} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle y^{0} = 4 } können über den Lagrange-Ansatz berechnet werden.
Berchnung des Substitutionseffektes: Kompensiertes Einkommen (Einkommen, das es erlaubt, das alte Güterbündel zu neuen Preisen zu erwerben): Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle E^{1} = p_{x}^1x(p_{x}^0,p_{y},E^0) + p_{y}y(p_{x}^{0}) = 320}