Haushaltsoptimum
Definition
Das Haushaltsoptimum ist die Konsumentscheidung eines Konsumenten, die er von allen möglichen am stärksten präferiert. Der Nutzen ist in diesem Punkt maximiert und ein höheres Niveau kann aufgrund der Budgetrestriktion nicht erreicht werden.
Das Haushaltsoptimum grafisch
Das Haushaltsoptimum liegt im Tangentialpunkt der Budgetgeraden und der Indifferenzkurve. Dies hängt mit den Axiomen der Nutzentheorie zusammen. Aufgrund der Monotonie/Lokale nicht Sättigung ist es für den Kosnumenten von allem so viel zu konsumieren, wie nur irgendwie möglich. Deshalb gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_1<I_2<I_3 }
. Ständen nur die drei Indifferenzkurven zur Auswahl, würder der Konsument entlang der dritten Indifferenzkurve konsumieren. Er ist jedoch in seinem Budget limitiert. Er kann nicht unendlich viel für seinen Konsum ausgeben, wenn er nur eine Summe E zur Verfügung hat. Der Konsum unterhalb der Budgetgeraden ist genauso möglich, wie der Konsum auf der Budgetgerade. Der Konsum überhalb der Budgetrestriktion ist nicht möglich, da hierfür ein größeren Budget nötig wäre.
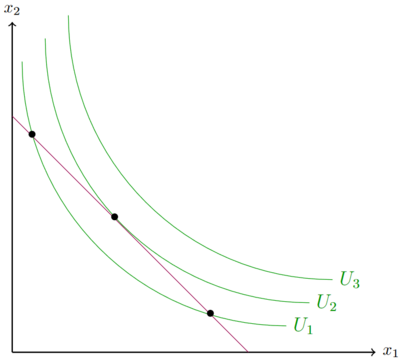
Indifferenzkurve eins, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_1 }
, ist nicht nutzenmaximal, selbst wenn der Konsument sein Budget vollständig ausgibt, existieren Konsumgüterbündel, die ein höheres Nutzenniveau bedeuten.
Das Haushaltsoptimum rechnerisch
Hicksche und Marshallsche Nachfrage
MC Fragen