Präferenzen und Indifferenzkurven
Individuen zeigen in ihrem Konsumverhalten Präferenzen. Diese Präferenzen werden durch ihre Nutzenfunktionen definiert, diese beschreibt den Nutzen den ein Individuum aus dem Konsum von Güterkombinationen erhält. Bei einer gleichen Güterkombination und unterschiedlichen Konsumentenpräferenzen kann sich daher das Nutzenniveau zwischen Individuen unterscheiden.
Präferenzen und Nutzenfunktion
Eine jede Marktteilnehmerin und ein jeder Marktteilnehmer verfügen über Präferenzen. Ein Mensch der Vegetarier ist, kauft zum Beispiel kein Fleisch. Für ein Filmabend gibt es Menschen, die lediglich salzige Snacks konsumieren, oder auch welche, für die nur süße Snacks in Frage kommen. Es gibt jedoch auch sicherlich Menschen, denen es egal ist welche Art der Snacks zu sich nehmen.
Um all diese Präferenzen abbilden zu können werden Nutzenfunktionen modelliert. Hierfür wird sich der Ordinalen Nutzentheorie und nicht der kardinalen Nutzentheorie bedient. Je nach Präferenzen sehen die Nutzenfunktionen unterschiedlich aus. In jedem Fall sind sie jedoch abhängig von jedem zu betrachteten Gut und der Anzahl der davon konsumierten Einheiten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(x_{1}, x_{2}, x_{3}, ..., x_{n}) }
. Der Einfachheit halber, und um die Nutzenfunktion grafisch darstellen zu können, beschränken wir uns auf den zwei-Güter-Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(x_{1}, x_{2}) }
. Als Beispiel sollen uns die beiden Güter C und F dienen, die mit folgender Nutzenfunktion abgebildet werden sollen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(F,C)=F^{1/3}*C^{2/3} }
Die Nutzenfunktion kann als normale bivariate Funktion gelesen werden. Anders als im univariaten Fall ist die Funktion von zwei Variablen abhängig.
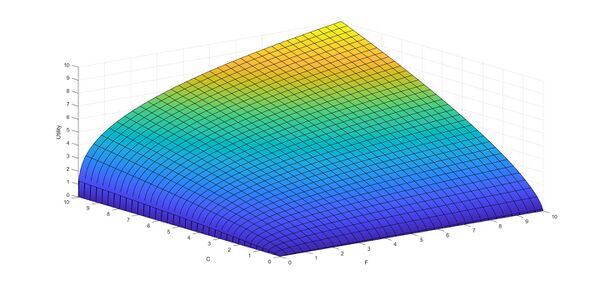
Indifferenzkurven
Eine veränderte Möglichkeit der Darstellung von Nutzenfunktionen sind Indifferenzkurven. Wie der Name bereits aussagt, sind Konsumenten entlang dieser Kurve indifferent in der Konsumentscheidung. Sie erfahren aus den Güterkombinationen, die auf der Indifferenzkurve liegen einen konstant gleich großen Nutzen. Je nach Nutzenniveau liegen die Indifferenzkurven verschoben. Im Beispiel von oben sehen die Indifferenzkurven wie folgt aus:
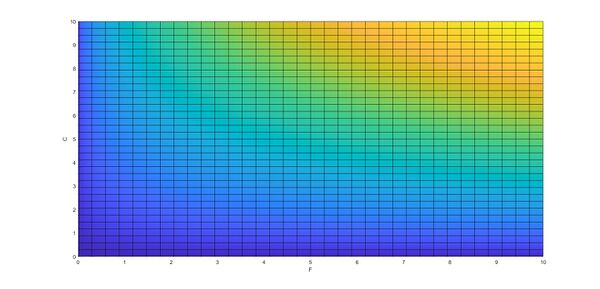
In der Grafik oben sind verschiedene Farbverläufe zu sehen, die an verschobene konvexe Funktionen erinnern. Mathematisch erlangt man die Indifferenzkurven, in dem der Nutzen U konstant gehalten (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar{U} }
) und nach einer Variablen umgestellt wird (welche auf der horizontale Achse abgebildet werden soll). In der Nutzenfunktion von eben sieht das wie folgt aus:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \bar{U}=F^{1/3}*C^{2/3} }
|:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{\bar{U}}{F^{1/3}}=C^{2/3} }
|Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (...)^{3/2} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle C=(\frac{\bar{U}}{F^{1/3}})^{3/2} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle C=\frac{\bar{U}^{3/2}}{F^{1/2}} }
Je nach Nutzenniveau ergibt sich für jeden F Wert einen anderen C Wert.
Die Steigung der Indifferenzkurve bzw. Grenzrate der Substitution
Entlang einer konvexen Indifferenzkurve verändert sich die Steigung der Indifferenzkurve. Für den weiteren Verlauf soll folgende Indifferenzkurven als Beispiel dienen:
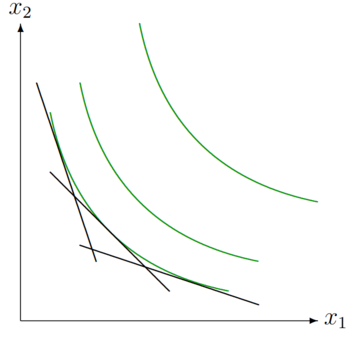
Bei einem geringen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{1} }
Wert ist der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{2} }
Wert hoch. Das dazugehörige Konsumgüterbündel befindet sich nahe der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{2} }
Achse. Hier ist die Funktion stark fallend (betragsmäßig sehr steil), da beide Güter einen abnehmenden Grenznutzen haben. Je größer der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{1} }
Wert wird, desto weniger stark fällt die Funktion. Die Steigung der Indifferenzkurve nimmt betragsmäßig also ab.
Um die Steigung interpretieren zu könne muss die Bedeutung der Indifferenzkurve herangezogen werden. Entlang der Indifferenzkurve ist der Nutzen konstant. In dem marginal zu betrachtenden Punkt ist ein Konsument bereit die Güter im Verhältnis der Steigung auszutauschen, da er so seinen Nutzen behält. Ist die Steigung beispielsweise -2, ist er bereit eine marginale Einheit von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{1} }
für zwei Einheiten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{2} }
zu tauschen. Je nach Position auf der Indifferenzkurve verändert sich auch das Verhältnis, das der Konsument verlangt. Die Steigung der Indifferenzkurve entspricht dem Verhältnis, zu dem ein Konsument bereit ist, die Güter zu tauschen (Austauschverhältnis). Dies wird auch Grenzrate der Substitution (GRS), beziehungsweise Marginal Rate of Substitution (MRS) genannt.
Mathematisch kann bei der Bestimmung des Haushaltsoptimums gezeigt werden, dass die GRS dem Grenznutzenverhältnis der beiden Gütern entspricht.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GRS_{x_{1},x_{2}}=\frac{\frac{\partial U}{\partial x_{1}}}{\frac{\partial U}{\partial x_{2}}} }
Indifferenzkurven der Güterarten
Die Indifferenzkurven der verschiedenen Güterarten unterscheiden sich je nach Präferenzen. Häufig wird zwischen den folgenden Güterarten und ihren Indifferenzkurven unterschieden:
Perfekte Substitute
Die Nutzenfunktion von Perfekten Substituten kann zum Beispiel wie folgt aussehen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(x_{1},x_{2})=ax_{1}+bx_{2} }
, wobei a und b beliebige Konstanten sind. Indifferenzkurven von Perfekten Substituten weisen als Eigenschaft auf, dass sie die Achsen berühren und einen linearen Verlauf haben. Das bedeutet: sie haben eine konstante GRS, da der Grenznutzen beider Güter konstant ist.
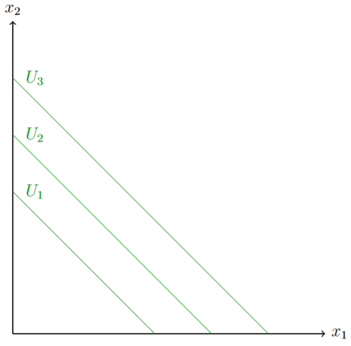
In der Abbildung gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{3} > U_{2} > U_{1} }
Perfekte Komplemente
Die Nutzenfunktion von Perfekten Komplementen kann zum Beispiel wie folgt aussehen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(x_{1},x_{2})=min\{ax_{1},bx_{2}\} }
, wobei a und b beliebige Konstanten sind. Grafisch sind die Indifferenzkurven in L Form, es wird auch häufig von Leontief Präferenzen gesprochen. Diese Güter stiften nur einen Nutzen, wenn sie in einem festen Verhältnis konsumiert werden. Klassische Beispiele sind Schuhe, Socken oder Handschuhe.
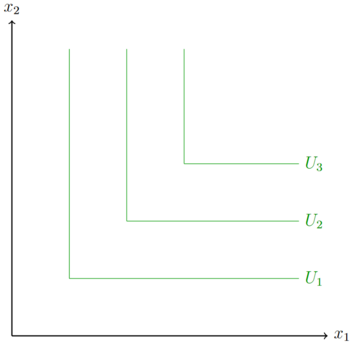
In der Abbildung gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{3} > U_{2} > U_{1} }
Imperfekte Subtitute
Die Nutzenfunktion von Imperfekte Substitute kann zum Beispiel wie folgt aussehen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle U(x_{1},x_{2})=x_{1}^{a}*x_{2}^{b} }
, wobei a und b beliebige Konstanten sind.
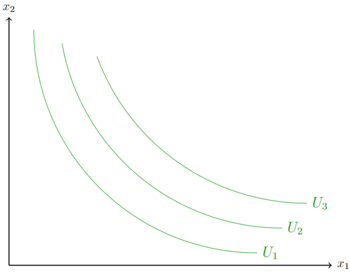
In der Abbildung gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{3} > U_{2} > U_{1} }
MC Fragen
