Edgeworth-Box
Definition
Die Edgeworth-Box ist die grafische Darstellung einer geschlossenen Volkswirtschaft mit zwei Haushalten und zwei unterschiedlichen Gütern. Die Güter sind in ihrer Anzahl begrenzt.
Die Box
Die Box der Edgeworth-Box ist die grafische Darstellung, wie zwei begrenzte Güter zwischen zwei Haushalten aufgeteilt werden können. Die Menge des Haushaltes A ist hierbei abhängig wie viel der Haushalt B von diesem Gut konsumiert. Angenommen von einem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
existieren 10 Einheiten. Wenn Haushalt B von den 10 Haushalten 7 konsumiert, kann Haushalt A nur noch 3 Einheiten kosnumieren.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1^{A}=x_1^{max}-x_1^{B}=10-7 }
Beziehungsweise Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1^{max}=x_1^{A}+x_1^{B} }
Dasselbe gilt für das andere Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
. Die beschriebenen Relationen der Konsummenge kann in einem Viereck dargstellt werden.
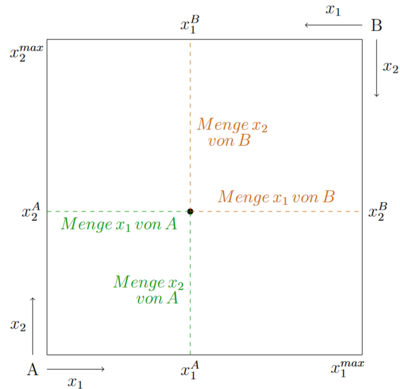
Die horizontale Gerade beschreibt die Menge von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
. Je weiter rechts der Konsumpunkt liegt, desto mehr Konsumiert A von diesem Gut und desto weniger B. Die vertikale Gerade beschreibt die Aufteilung des Gutes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
. Je weiter oben der Konsumpunkt liegt, desto mehr konsumiert A von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
und desto weniger B.
Präferenzen in der Edgeworth-Box
Haushalte weisen in ihrem Konsumverhalten Präferenzen auf. Die grafische Darstellung der Präferenzen erfolgt über Indifferenzkurven entlang derer das Nutzenniveau konstant ist.
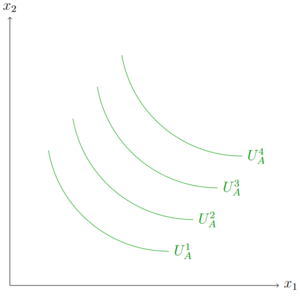
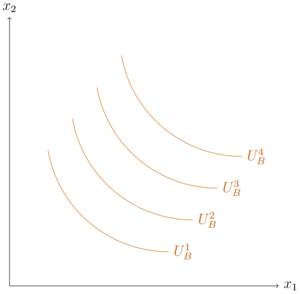
Im Weiteren sollen nicht nur die Präferenzen eines Haushalts, sondern auch die Präfernzen eines zweiten Haushalts betrachtet werden. Um die Präferenzen in der Edgeworthbox darzustellen, wird das Kordinatensystems eines Haushalts um 180 Grad gedreht.
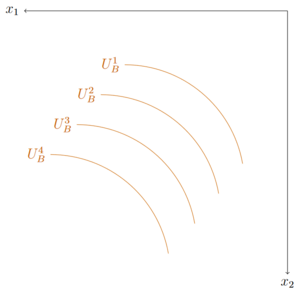
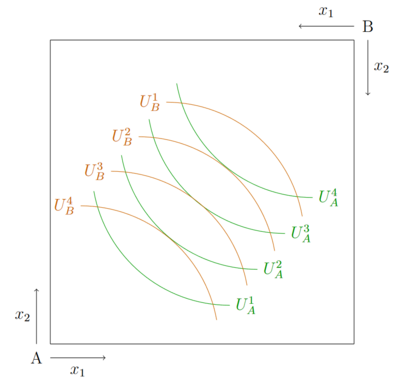
Werden die Koordinatensysteme des Haushalts A und des Haushalts B mit den jweiligen Präferenzne übereinandergelegt, entsteht die Edgeworth-Box. Anhand dieser wird deutlich, in welchen Punkten es effizint ist zu konsumieren. In der Edgeworth-Box gibt es unendlich viele Indifferenzkurven, von denen einige unte eingezeichnet sind. Einige Indiffernzkurven des Haushalts A tangieren jeweils eine Indifferenzkurve des Haushalts B.