Arbeit-Freizeit Entscheidung
Die Arbeit-Freizeit-Entscheidung ist die Entscheidung eines Haushalts zwischen Arbeit (F) und Freizeit (L) mit einer Zeitrestriktion und einer Budgetrestriktion.
Entscheidungsmöglichkeiten
Der Haushalt wählt zwischen Arbeit (L) und Freizeit (F). Entscheidet sich der Haushalt für die Arbeit, erhält er in der Zeit einen Lohn w, den er für seinen Konsum (C) ausgeben kann. Entscheidet er sich für die Freizeit, kann er in derselben Zeit nicht arbeiten und Geld für seinen Konsum verdienen, doch erfährt er einen Nutzen aus der Zeit, in der er nicht arbeitet. Die Arbeitszeit korreliert vollständig mit der Möglichkeit den Konsum auszuweiten.
Die Nutzenfunktion ist daher nur abhängig von seinem Konsumniveau und der Stundenanzahl, in der er Freizeit genießt (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U(C,F)}
). In der Regel verhalten sich Konsum und Freizeit als Imperfekte Substitute. Der Haushalt kann demnach nicht vollständig auf Konsum, aber auch nicht vollständig auf Freizeit verzichten. Der Haushalt maximiert seinen Nutzen durch die optimale Verteilung seiner verfügbaren Zeit zwischen Freizeit und Arbeit.
Budgetrestriktion
In einem Ein-Perioden-Modell gibt der Haushalt sein Einkommen vollständig aus, um seinen Nutzen zu maximieren. Die Unterschiede zu der Budgetrestriktion im Zwei-Güter-Modell liegen darin, dass nicht zwischen dem Konsum verschiedener Güter unterschieden wird und darin, dass das Einkommen nicht exogen ist und erwirtschaftet werden muss.
Das erwirtschaftete Einkommen muss den gesamten Konsumausgaben entsprechen. Das Einkommen ist gleich dem Stundenlohn multipliziert mit der Stundenanzahl, die gearbeitet wird. Beträgt der Stundenlohn beispielsweise 13€ und ein Haushalt arbeitet 8 Stunden, liegt das verfügbare Einkommen bei 104€. Verfügt ein Haushalt über ein Vermögen (M), erhöht sich das Einkommen um das Vermögen
Verfügbares Einkommen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Einkommen=Stundenlohn*Arbeitszeit+Verm \ddot o gen=wL+M }
Konsumausgaben: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Konsumausgaben=Preis*Konsumniveau=pC }
Budgetrestriktion: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle wL+M=pC }
Zeitrestriktion
Der Haushalt ist nicht nur in seinem Budget begrenzt, sondern auch in seiner Zeit. In der Zeit, in der er Freizeit genießt, kann er nicht arbeiten und vice versa. Er befindet sich somit in einem Trade-off. Die Intuition der Zeitrestriktion ist die gleiche wie die der Budgetrestriktion. Das Zeitbudget (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar{Z}}
) wird durch die beiden Möglichkeiten (Arbeit und Freizeit) vollständig ausgegeben.
Zeitbudget: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Zeitbudget=\bar{Z} }
Zeitausgaben: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Zeitausgaben=F+L }
Zeitrestriktion: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar{Z}=F+L }
Die modifizierte Budgetrestriktion
Der Haushalt unterliegt zwei Restriktionen:
(i) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle wL+M=pC }
(ii) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar{Z}=F+L }
Die beiden Restriktionen können zu einer zusammengefasst werden. Da in beiden Gleichungen L als Variable vorkommt, kann mit L substituiert werden. (ii) nach L umgestellt ergibt:
(ii)' Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L=\bar{Z}-F }
(ii)' in (i) eingesetzt ergibt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w(\bar{Z}-F)+M=pC }
Die obige Gleichung beinhaltet beide Restriktionen. Die Zeit, die gearbeitet wird, entspricht der verfügbaren Zeit abzüglich der Freizeit. Multipliziert mit dem Lohn w ergibt sich das verfügbare Einkommen, das im Optimum vollständig für den Konsum ausgegeben wird.
Zur grafischen Darstellung muss die Budgetrestriktion nach C oder F umgestellt werden. Alle anderen Ausdrücke in der Restriktion sind Konstanten. Die Funktionsgleichung der modifizierten Budgetrestriktion ist beschrieben in
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C(F)=\frac{w(\bar{Z}-F)+M}{p} }

Aus der oben skizzierten modifizierten Budgetrestriktion werden die Zusammenhänge zwischen den Konstanten () deutlich. Erhöht sich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M }
oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar{Z} }
, verschiebt sich die Budgetgerade parallel nach außen. Erhöht sich der Stundenlohn, erhöht sich der C-Achsenabschnitt und der F-Achsenabschnitt verringert sich. Erhöht sich der Konsumpreis p, verringert sich der C-Achsenabschnitt und der F-Achsenabschnitt erhöht sich. Die letzten beiden Zusammenhänge verdeutlichen die Opportunitätskosten der jeweiligen Opportunität. Die Opportunitätskosten für eine Stunde Freizeit ist der entgangene Stundenlohn.
Optimierung
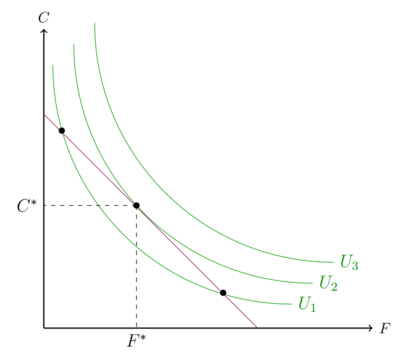
Die Nutzenmaximierung bei der Arbeit-Freizeit-Entscheidung funktioniert wie bei der Optimierung im Zwei-Güter-Modell. Grafisch liegt das Optimum im Tangentialpunkt der Indifferenzkurve und der modifizierten Budgetgeraden.
Rechnerisch muss die Zielfunktion mit der Nebenbedingung maximiert werden. Eine Möglichkeit stellt das Langrangeverfahren dar. Die Lagrangefunktion lautet
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathcal{L} (C,F,\lambda)=U(C,F)+\lambda (M+w(\bar{Z}-F)-pC) }
MC Fragen
