Inputeffizienz, Konsumeffizienz und Outputregel

Der erste Hauptsatz der Wohlfahrtsökonomik besagt, dass alle Konkurrenzmarktgleichgewichte pareto-effizient sind. Dies kann mittels Edgeworth-Box für den Handel auf der Konsumentenseite gezeigt werden. Im Weiteren soll gezeigt werden, dass der erste Hauptsatz auch für die Produktion im Wettbewerbsgleichgewicht, den Input in Wettbewerbsgleichgewichten, die Allokation der Güter und den Output in Wettbewerbsgleichgewichten gilt.

Effiziente Allokation der Güter

Güter werden entsprechend des ersten Haupsatz der Wohlfahrtökonomie effizient allokiert. Um dies zu veranschauchlichen soll ein einfaches Beipsiel mit zwei Gütern (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } ) dienen. Ein Unternehmen kann eben diese zwei Güter produzieren. Die Frage ist, wie das Unternehemn in der Gewichtung der Produktionsmengen der jeweiligen Güter entscheidet. Hierbei liegt ein spezielles Austauschverhältnis der beiden Güter vor. Es kann zum Beispiel der Fall sein, dass ein Produzent ein Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } weniger produziert und dadurch ein Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } mehr. Aber auch andere Verhältnisse sind möglich. Die verschiedenen Fälle lassen sich jeweils durch eine Funktion darstellen. Ein Unternehmen kann sich dementsprechend zu einem festgelegten Verhältnis zwischen der Produktion für ein Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } und einem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } entscheiden. Für die Produktion benötigt das Unternehmen eine Art "Budget", dass es für die Produktion verwenden kann. Es handelt sich selbstverständlich nicht um ein Budget wie im Haushaltsoptimum. Es stammt vielmehr von einer Anfangsausstattung aller Inputfaktoren. Ein Unternehme kann beispielsweise mit $F(K,L)=K^{2}+L^{2}$ un einer Anfangsausstattung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (K,L)=(10,10) } 200 auf die Produktion der beiden Güter aufteilen. Alle möglichen Kombinationen der Produktion sei dann in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1^2+x_2^2=200 } beschrieben. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a^2+b^2 } beschreibt, wie das Unternehmen zwischen den beiden Gütern in der Produktion wechseln kann. Dies zeigt sich durch das Umstellen der Formel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1^2+x_2^2=200 } . Umgestellt nach einer der beiden Gütern, kann durch einfaches einsetzen herausgefunden werden, wie viel das Unternehmen von dem einen Gut produzieren kann, wenn es von dem anderen Gut eine bestimmte Menge, die eingesetzt wird, produziert. Umgestellt nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } ergibt sich:
$x_{2}(x_{1})={\sqrt {200-x^{1}}}$.
Produziert das Unternehmen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } 10 Einheiten, kann es von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } nur 10 Einheiten produzieren. Die oben umgestellte Funktion ist auch grafisch darstellbar und gibt an, wie viel der beiden Güter jeweils abhängig vom anderen produziert werden kann. Diese Funktion wird auch Transformationskurve genannt:


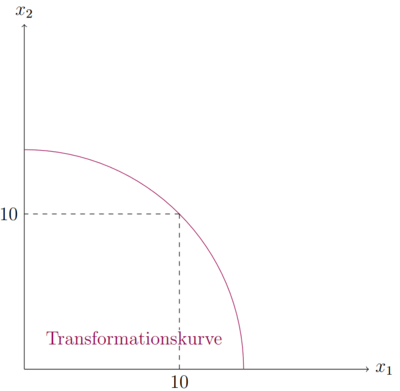
Die Transformationskurve wurde beispielhaft für ein Niveau von 200 eingezeichnet. Für andere Niveaus verändern sich jeweils die Achsenabschnitte. Alle Produktionskombinationen auf oder unter der Transformationskurve sind realisierbar. Alles außerhalb der Kurve ist nicht möglich. Entlang der Kurve kann abgelesen werden, wie viele marginale Einheiten eines Gutes weniger produziert werden müsen, um von dem anderen eine marginale Einheit mehr zu produzieren. Dies lässt sich durch Tangenten grafisch oder durch die Grenzrate der Transformation rechnerisch bestimmen. Die Intuition ist hierbei ähnlich zu der Grenzrate der Substitution (GRS) und der Grenzrate der technischen Substitution (GRTS). Die abgebildete Grenzrate der Transformation nimmt betragsmäßig zu. Angenommen von dem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } wird nichts produziert. Es benötigt nur sehr wenige Einheiten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } , die eingespart werden müssen um eine Einheit von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } zu produzieren. Je mehr von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } produziert wird, desto mehr Einheiten von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } müssen eingespart werden. Dies hängt vorallem mit dem Grenzprodukt, bzw. der Annahme der steigenden Grenzkosten zusammen. Je mehr von einem Gut produziert wird, desto größer sind die Grenzkosten. Das Einsparen einer Einheit bei einem hohen Produktionsniveau reduziert die Grenzkosten dieser Einheit. Die freigewordenen Ressourcen können in die Produktion von dem anderen Gut gehen, das bei einem geringeren Produktionsniveau häufig geringere Grenzkosten hat. Dies hat zur Folge, dass die GRT gleich dem Grenzkostenverhältnis ist.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GRT=\frac{\frac{\part 200=x_1^2+x_2^2}{\part x_2}}{\frac{\part 200=x_1^2+x_2^2}{\part x_1}} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Leftrightarrow } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GRT=\frac{GK_1}{GK_2}=\frac{MC_1}{MC_2} }

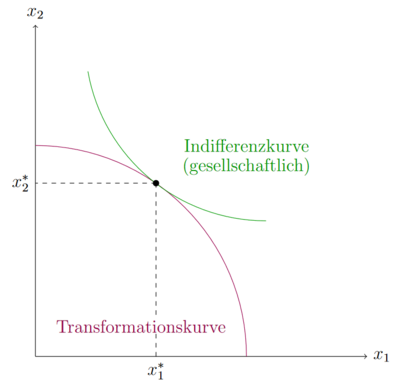
Die Ausführungen oben zeigen, wie ein Unternehmen (oder eine ganze Industrie) zwischen der Produktion zweier Güter wählen kann. Wie einfach der Wechsel von Produktion des Gutes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 } zu Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 } ist zeigt sich in der GRT. Jedoch stellt sich weiterhin die Frage, welche Aufteilung optimal ist. Recht intuitiv unter den Standradannehmen ist, dass die optimale Menge auf der Tranformationskurve liegt. Ein Unternehmen wird sehr wahrscheinlich so viele Güter wie mölglich produzieren und damit verkaufen wollen. Dass es jedoch auch für die Konsumenten in einer gesellschaftlichen Sichtweise optimal ist, wenn das Unternehmen auf der Transformationskurve produziert, zeigt die weitere Ausführung. Hierfür sollen Indifferenzkurven aus gesellschaftlicher Sicht modelliert werden. Unter den Annahmen über Präferenzen ist eine hohe Konsummenge besser, als eine leicht gerinigere. Die Gesellschaft versucht also als ganzes auf eine möglichst hohe Indifferenzkurve zu gelangen. Dise liegt im Tangentialpunkt der Indifferenzkurve mit der Transformationskurve. Es muss also gelten
$GRT=GRS$