Elastizitäten
Definition
Elastizitäten betrachten die prozentuale Änderung einer Variablen infolge einer Änderung einer anderen Variablen um ein Prozent. Im Falle der Preiselatizität des Angebots wird sich angeschaut, um wie viel Prozent sich die nachgefragte Menge verändert, wenn sich der Preis um einen Prozent verändert.
Herleitung über den Differenzenqoutienten
An dieser Stelle gilt es die Intuition der ELastizität anhand der Preiselastizität der Nachfrage zu verstehen. Es soll um die Frage gehen, wie viel mehr, bzw. weniger von einem Gut navhgefragt wird, wenn sich der Preis z.B. erhöht. Hierbei gilt es direkt darauf zu achten, welchen Bezugspunkt wir vom Preis nehmen. Die Preiserhöhung eines Luxusautos um 5€ wird vermutlich weniger Einfluss auf die nachgefragte Menge haben, als eine Erhöhung um 5€ des Preises eines Bleistifts. Damit die Veränderung vergleichbar wird, schauen wir uns die Prozentuale Veränderung an. Diese Überlegung steckt so auch in der Formel: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{ P_{2}-P_{1}}{P_{1}} }
. Die Absolute Preisänderung relativ zum alten Preis. Wenn der neue Preis höher ist als der alte Preis, ist hat sich der Preis prozentual vergrößert.
Die selbe Überlegung stellen wir bei der Änderung der nachgefragten Menge an. Wir brauchen einen Bezugspunkt. Eine Reduktion der nachgefragten Menge um 5 Einheiten ist etwas anderes wenn vorher sehr viel nachgefragt wird, als wenn wenig nachgefragt wird. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{ Q_{2}-Q_{1}}{Q_{1}} }
.
Im folgenden werden wir die absoluten Änderungen als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Delta }
schreiben: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{ Q_{2}-Q_{1}}{Q_{1}}=\frac{\Delta Q}{Q} }
Setzen wir nun die prozentuale Änderung der Menge im Verhältnis zur prozentualen Änderungen des Preises, bekommen wir eine Kennziffer, die beschreibt um wie viel prozent sich unsere Menge ändert, wenn sich der Preis um 1 Prozent ändert:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \frac{\frac{\Delta Q}{Q}}{\frac{\Delta P}{Q_{P}}}=\frac{\Delta Q}{\Delta P} \frac{P}{Q} }
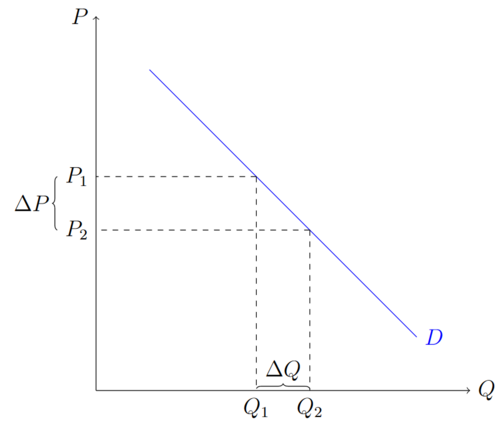
Da diese Kennziffer ungenauer wird, je größer die absoluten Änderungen sind, lassen wir unser Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta }
immer kleiner werden (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \Delta \to 0 }
). Diese Vorgehensweise entspricht dem Differenzenquotienten, die aus der Differentialrechnung (dem Ableiten) bekannt sein sollte. Dies führt uns zu folgender Gleichung für die Preiselastizität der Nachfrage: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon=\frac{\partial Q}{\partial P} \frac{P}{Q} }
Preiselastizität der Nachfrage
Die Preiselastizität der Nachfrage betrachtet die prozentuale Änderung der nachgefragten Menge auf eine ein prozentige Änderungen des Preises. In der Regel sollte auf eine Preiserhöhung eine Reduzierung der nachgefragten Menge erfolgen. Dies ist der Grund, warum es in mancher Literatur neben unserer bekannten Gleichung auch andere Formeln gibt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon=\frac{\partial Q}{\partial P} \frac{P}{Q} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon= - \frac{\partial Q}{\partial P} \frac{P}{Q} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle \epsilon=| \frac{\partial Q}{\partial P} \frac{P}{Q} | }
Zu beachten gilt, dass die Elastizität nicht der Steigung entspricht. Entlang einer linearen Nachfragefunktion verändert sich die Steigung nicht, die Preiselastizität schon. Bei einem hohen Preis wird nur eine geringe Menge nachgefragt. Verändert sich der Preis, so ist die prozentuale Änderung eher gering (wir nehmen von sehr viel etwas weg). Die prozentuale Änderung der Menge ist jedoch sehr groß (wir nehmen von sehr wenig etwas weg). Entlang der linearen Nachfragefunktion ändert sich dementsprechend die prozentuale Veränderung und damit auch die Preiselastizität. Folgende Grafik sollte dies verdeutlichen:
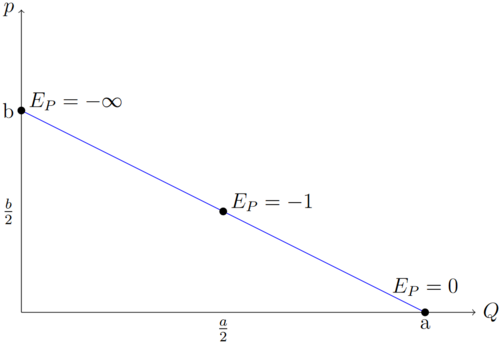
Preiselastizität des Angebots
Besonderheiten der Preiselastizität
auf Bogenelastizität eingehen, unelastisch etc
Kreuzpreiselastizität
Einkommenselatizität der Nachfrage
MC Fragen