Effizienz
In unserem Modell ist jedes Marktgleichgewicht eines perfekten Wettbewerbs effizient. Vor diesem Hintergrund gilt es zu wissen, was mit Effizienz gemeint ist und welche Formen der Effizienz wir betrachten.
Effizienz in Wettbewerbsmärkten
Um die Effizienz in einem Markt zu bewerten wird die aggregierte Konsumentenrente und Produzentenrente herangezogen. Wenn diese maximiert wird, spricht man von ökonomischer Effizienz. Hierbei gilt es zu beachten, dass es keine Rolle spielt wie die Aufteilung der jeweiligen Renten ist. Im Fall der perfekten Preisdidskriminierung, also ein Fall, in dem die Konsumentenrente vollständig abgeschöpft und zur Produzentenrente wird, kann dennoch ökonomisch effizient sein. Ökonomische Effizienz sagt also nichts über eine gerechte Verteilung aus. Sobald ein Wohlfahrtsverlust entsteht kann ein Markt somit nicht mehr effizient sein, erst recht wenn ein Markt versagt, zum Beispiel bei Externalitäten.
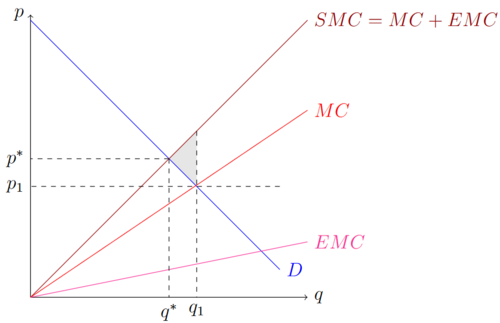
Eingriffe in das Marktgleichgewicht sind weitere Möglichkeiten, in denen ein Markt zur Ineffizienz neigt. Es ist wichtig an dieser Stelle anzumerken, dass hier zwischen politischen Entscheidungen und dem ökonomischen Effiziengedanken unterschieden wird. Neben der deskriptiven Aussage, dass Steuern zu einem Wohlfahrtsverlust führen und daher ineffizient sind, lassen sich außerdem positive Aussagen formulieren was daraus folgt. Eine Möglichkeit wäre zu sagen, dass Steuern daher nicht eingeführt werden sollten, eine andere Möglichkeit ist zu sagen, dass Steuern zu einem ineffizienten Marktergebnis führen, sie aber dafür einen anderen ebenfalls wichtigen Zweck erfüllen.
Inputeffizienz
Outputeffizienz
Pareto Effizienz
Eine Situation ist pareto effizient, sobald niemand besser gestellt werden kann ohne einen anderen dadurch schlechter zu stellen. Dies lässt sich sehr gut in einer 2 2 Spielmatrix verdeutlichen.
| 1|2 | C | D |
|---|---|---|
| A | 3, 3 | 6, 0 |
| B | 0, 6 | 1, 1 |
Spieler 1 kann nur zwischen A und B entscheiden und Spieler 2 nur zwischen C und D. Angenommen wir untersuchen (A, C). Der Payoff für Spieler 1 beträgt 3, der für Spieler 2 ebenfalls. Für Spieler 1 wäre (A, D) besser, da er hier einen Payoff von 6 hätte (mal davon abgesehen, dass er alleine nicht bestimmen kann welcher Payoff herauskommt). Spieler 2 hätte bei (A, D) allerdings nur einen Payoff von 0, was geringer ist als vorher. (A, C) wäre also pareto effizient, da keiner der beiden Spieler einen größeren Payoff erlangen kann ohne den anderen schlechter zu stellen.
Der einzige Outcome, der nicht pareto effizient ist, ist (B, D). In diesem haben beide Spieler einen Payoff von 1. Der (A, C) Outcome stellt Spieler 1 besser ohne Spieler 2 schlechter zu stellen, im Gegegnteil, Spieler 2 wird ebenfalls besser gestellt.
Hier dann Beispiel aus der Edgeworthbox
