Budgetrestriktion und Budgetgerade
Definition
Die Budgetgerade ist die Kombination aller möglichen Güterbündeln, bei denen die ausgegebene Geldsumme gleich dem Einkommen ist.
Konsumausgaben
Die Konsumausgaben für ein beliebiges Gut X stellen sich aus der konsumierten Mengen für dieses Gut und seinem Preis zusammen. Konsumausgaben von xFehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle =p_{x}*x }
.
Um die gesamten Konsumausgaben zu erlangen, muss über die Konsumausgaben der einzelnen Güter aufsummiert werden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C=\sum_i^N p_{i}*X_{i} }
In unseren Beipielen begrenzen wir uns häufig auf ein Zweigütermodell, sodass die Konsumausgaben wie folgt aussehen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle Konsumausgaben=p_{1}x_{1}+p_{2}x_{2} }
Budgetrestriktion
Gehen wir in unserem Modell weiter davon aus, dass wir ein begrenztes Budget E zur Verfügung haben, das wir maximal ausgeben können. Der Konsum unterhalb unseres Budgets ist möglich, überhalb unseres Budgets können wir jedoch nicht konsumieren, da dies außerhalb der Budgetmöglichkeiten liegt. Die Konsumausgaben müssen daher geringer oder gleich unserem Budget sein.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{1}x_{1}+p_{2}x_{2}}
≤
Budgetgerade
Die Budgetrestriktion lässt sich in ein Diagramm zeichnen. Hierfür muss man die Budgetrestriktion mit der Hilfe von Äquivalenzumformungen nach der Variablen umstellen, die auf der vertikalen Achse abgebildet werden soll. Der Einfachheit halber gehen wir nicht mehr von einer Ungleichung, sondern von einer Gleichung aus. Dies ist allerdings nicht zwingend notwendig und lässt sich auch ohne Vereinfachung durchführen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{1}x_{1}+p_{2}x_{2}=E }
|Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle -p_{1}x_{1} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle p_{2}x_{2}=E-P_{1}x_{1} }
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle :p_{2} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_{2}=\frac{E}{p_{2}}-\frac{p_{1}}{p_{2}} }
Grafisch lässt sich die Budgetgerade dann wie folgt darstellen:
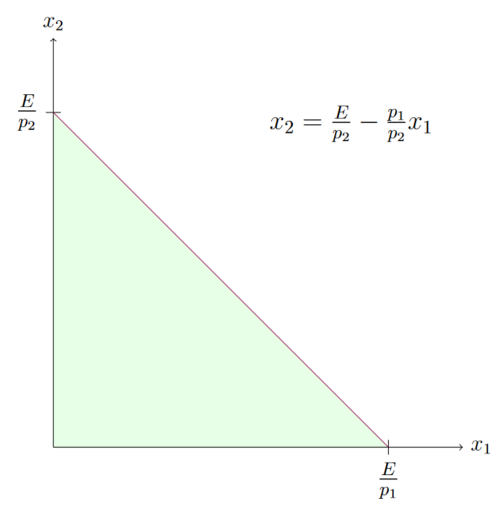
Auf der Geraden selbst wird das Budget vollständig ausgegeben. In der grün markierten Fläche wird unterhalb des Budgetmaximums konsumiert. Überhalb der Budgetgeraden ist ein Konsum mit dem gegebenen Budget E nicht möglich.
Veränderung der Budgetgeraden
Es gibt zwei Möglichkeiten weshalb sich die Budgetgerade in unserem einfachen Modell verändern könnte. Der Erste Grund ist die Veränderung von Preisen und der zweite Grund die Veräderung vom Budget E.
Veränderung der Preise
Wie sich die Budgetgerade verändert wenn sich die Preise verändern lässt sich sehr gut in den Achsenabschnitten sehen. Die Achsenabschnitte stellen den maximalen Kosnum eines Guts bei gleichzeitigem Nichtkonsum des anderen Guts dar. Die Preise des nicht konsumierten Guts haben keinen Einfluss auf den Achsenabschnitt des anderen Guts. Sollte sich der Preis eines Guts verändern das nicht konsumiert wird, verändert sich das Konsumniveau des anderen Guts nicht. Die Veränderung des Preises eines Guts verschiebt somit nur den eigenen Achsenabschnitt. In der Abbildung gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p'' > p' > p }
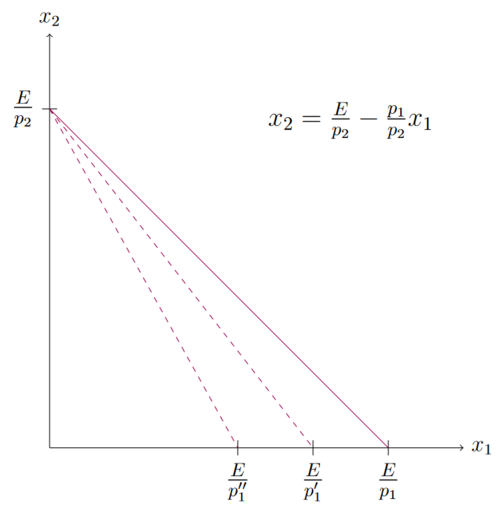
Veränderung des Budgets
Wie sich die Budgetgerade bei veränderten Budget verändert lässt sich am besten in der Geradengleichung sehen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle x_{2}=\frac{E}{p_{2}}-\frac{p_{1}}{p_{2}} }
. Das veränderte Budget hat keinen Einfluss auf die Steigung der Budgetgeraden, lediglich auf die Achsenabschnitte. Je kleiner das Budget ist, desto weiter wird die Budgetgerade parallel zum Ursprung verschoben. In der Abbildung gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\textstyle E > E' > E'' }
.
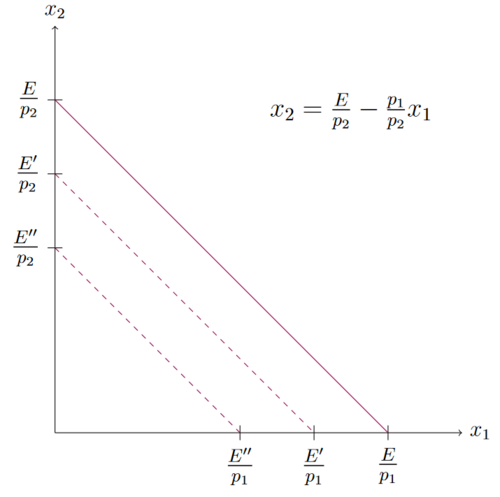
MC Fragen
