Risiko und Risikoeinstellung

Definition

Risiko bezieht sich auf Situationen, in denen alle möglichen Ergebnisse aufgeführt werden können und die Wahrscheinlichkeit des Eintretens aller Ergebnisse bekannt ist. Demnach wird im Folgenden zwischen der subjetiven und der objektiven Wahrscheinlichkeit differenziert und die objektive Wahrscheinlichkeit als Kennziffer herangezogen.

Risiko

Konkludent zu der Definition des Risikos wird eine Sitution mit Risiko Lotterie genannt. Ein Beispiel einer Lotterie ist der Münzwurf mit Wetteinsatz. Die Wahrscheinlichkeiten für Kopf und Zahl sind mit jeweils 0,5 bekannt. Fällt die zuvor gewählte Seite wird der Einsatz gewonnen, fällt er auf die andere Seite ist der Einsatz verloren.
Beispiel: Daniel und Oskar wetten auf das Ergebnis eines Münzwurfs. Daniel tippt auf Kopf und Oskar auf Zahl. Derjenige dessen Seite oben liegt erhält von dem anderen den Wetteinsatz von 10€. Allgemein kann eine solche Lotterie X in folgender Form dargestellt werden: $X=(x_{1},p_{1};x_{2},p_{2};...x_{n},p_{n})$, wobei n $\in \mathbb {R}$ und p ≥ 0. $x_{i}$ stellt die Auszahlung dar, die mit einer Wahrscheinlichkeit $p_{i}$ eintritt. In dem Fall des Münzwurfs würde dies folgende Lotterie bedeuten X=(0, 0.5; 10, 0.5).

Entscheidung unter Unsicherheit

Um zu untersuchen wie Individuen unter Unsicherheit agieren muss von dem Münzwurf Beispiel abstrahiert werden. Als Beispiel dient nun eine Anlageoption, die mit bekannten Wahrscheinlichkeiten unterschiedliche Werte auszahlt. In der Frage wie das Individuum mit dem Risiko umgeht sind verschiedene Kennzahlen entscheidend.
Eine Kennzahl bildet hier der Erwartungswert, beziehungsweise der Nutzen des Erwartungswertes. Beispiel: Die Anlage bringt mit einer Wahrscheinlichkeit von 0.5 einen Gewinn von 5 und mit der Gegenwahrscheinlichkeit werden gehen die investierten 5 verloren, der Gewinn beträgt also -5. Die Anlage hat demnach einen Erwartungswert von 0. Genauso gut könnte das Individuum also veremintlich gar nicht investieren und sich dem Risiko nicht aussetzen. Die Investition in die Anlage ist jedoch nicht grundsätzlich irrational. Dafür ist der erwartete Nutzen aus der Lotterie wesentlich. Der Erwartungsnutzen betrachtet nicht die Überlegung welche Auszahlung, sondern welcher Nutzen von der Lotterie erwartet wird. Mit einer Wahrscheinlichkeit von 0.5 erfährt das Individuum einen Nutzen von der Auszahlung -5 [U(-5)] und mit einer Wahrscheinlichkeit 0.5 einen Nutzen von der Auszahlung 5 [U(5)]. Ist der Nutzen des Erwartungswertes U(0) größer als der Erwartungsnutzen, sollte das Individuum zum Beispiel nicht in die ANlage investieren.

Im Grunde werden in dem Beispiel zwei Anlagemöglichkeiten miteinander verglichen. Zum einen die Lotterie X=(0.5, -5; 0.5, 5) und zum anderen die Lotterie Y=(1, 0). Eine unsichere Anlagemöglichkeit mit einer sicheren, deren beider Erwartungswerte identisch bei 0 liegen. Dementsprechend können auch andere Lotterien miteinander verglichen werden, deren Erwartungswerte nicht identisch ist. Je nach Modellierung muss jedoch auf den Kontext geachtet werden um etwas über die Risikopräferenzen, die in der Nutzenfunktion dargestellt sind, sagen zu können. Entscheidet sich ein Individuum beispielsweise für eine Lotterie mit einem größeren Erwartungswert, so kann unter der Annahme der Rationalität keine Aussage über die Risikopräferenzen getätigt werden. Entscheidet sich jedoch ein Individuum für eine sicherere Option mit einem geringeren Erwartungswert und handelt dabei rational, ist diese Person risikoavers.

Risikofreude

Risikofreude ist die Präferenz für ein risikoreiches Einkommen gegenüber einem sicheren Einkommen mit dem gleichen Erwartunsgwert. Ein solches rationales Individuum erfährt demnach aus der unsicheren Lotterie einen größeren Nutzen, als aus der Auszahlung des Erwartunsgwertes. Der Erwartungsnutzen ist größer als der Nutzen des Erwatungswertes.

E[U] > U[E]

Grafisch ist dies durch eine konvexe Nutzenfunktion möglich. Mathematisch ist die zweite Ableitung der Nutzenfunktion größer 0:

${\textstyle {\frac {\partial ^{2}U(x)}{\partial ^{2}x}}}$ > 0



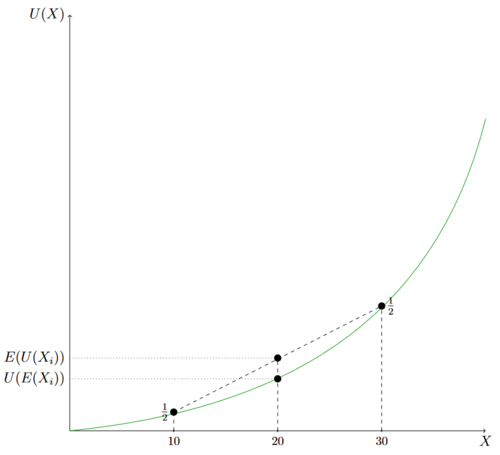
In dem grafischen Beispiel wird eine Lotterie X, X=(0.5, 10; 0.5, 30), betrachtet. Der Erwartungswert der Lotterie lautet 20 und der Nutzen des Erwartungswert liegt auf der grünen Nutzenfunktion. Mit einer Wahrsscheinlichkeit von 0.5 erfährt das Individuum einen Nutzen von 10, U(10), und mit einer Wahrscheinlichkeit von 0.5 einen Nutzen von 30, U(30). Der erwartete Nutzen der Lotterie liegt auf der gestrichelten Verbindungslinie von U(10) zu U(30) und ist größer als der Nutzen des Erwartunsgwertes. Ist die Wahrscheinlichkeitsverteilung der beiden Auszahlungen verändert, so liegt der Erwartungsnutzen weiterhin auf der gestrichelten Verbidnungslinie und ist in die Richtung der größeren Wahrscheinlichkeit verschoben. Die Risikoeinstellung des Individuums ist davon nicht betroffen.

Risikoneutralität

Eine risikoneutrale Person ist indifferenzt zwischen dem unsicheren Einkommen und dem sicheren Einkommen mit dem selben Erwartungswert. Der Erwartungsnutzen, also der Nutzen, der von drr Lotterie erwratet werden kann, ist genauso groß wie der Nutzen des Erwartungswertes.

E[U] = U[E]

Mathematisch müssen die beiden Werte identsich sein und auf der Nutzenfunktion liegen. Dies kommt durch eine lineare Nutzenfunktion zustande. Die zweite Ableitung der Nutzenfunktion muss gleich null sein