Vergleich Gewinnmaximum bei unterschiedlichen Marktformen
Im Einklang der Modellannahme des homo oeconomicus versuchen Unternehmen unabhängig von der Marktform, in der sie agieren, ihren Gewinn zu maximieren.
Die Gewinnfunktion
Gewinnfunktionen setzen sich aus dem Umsatz und den Kosten zusammen.
Bei einer konkaven Gewinnfunktion existiert ein Gewinnmaximum, an der die Steigung der funktion null ist. Eine marginale zusätzliche Einheit würde denn Gewinn nicht mehr erhöhen (≙ Die erste Ableitung der Gewinnfukntion muss gleich null sein)
Umgestellt bedeutet dies, dass der Grenzumsatz gleich den Grenzkosten sein muss. Da die Gewinnfunktion unabhängig von der Marktform aus dem Umsatz und den Kosten besteht, gilt die Grenzumsatz gleich Grenzkosten Relation ebenfalls immer. Der Unterschied besteht im Grenzumsatz und wie sich dieser zusammensetzt.
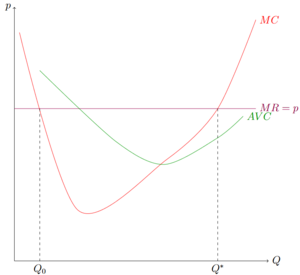
Gewinnmaximierung im perfekten Wettbewerb
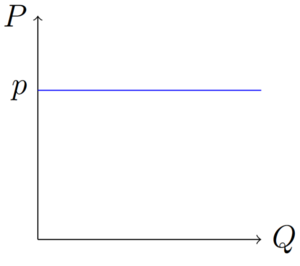
Im perfekten Wettbewerb sind alle Akteure, so auch die Produzenten, Preisnehmer. Sie sehen sich einer horizontalen Nachfragefunktion gegenüber, da sie für jede produzierte Einheit lediglich den Marktpreis verlangen können.