Produktionsfunktion und Isoquante

Definition

Die Produktionsfunktion gibt an, wie groß die Produktionsmenge ist, die mit gegeben Kombinationen der Inputs produziert werden kann. Die Umwandlung aller Inputs zu den produzierten Gütern wird als Produktionstechnologie bezeichnet. Die Inputs selbst werden auch als Inputfaktoren bezeichnet. Typische Inputfaktoren sind Arbeit (L) und Kapital (K).

Die Produktionsfunktion

Die Produktionsfunktion gibt an, mit welchen Inputfaktoren welche Menge produziert werden kann. Abhängig von der gewählten Technologie kann die Anzahl der Inputfaktoren und die Funktion selbst variieren. In der Literatur wird sich häufig auf zwei Inputfaktoren, Kapital (K) und Arbeit (L) beschränkt, doch können in anderen Produktionen durchaus eine veränderte Anzahl von Inputfaktoren benötigt werden.
$Q=F(K,L)$ beschreibt, dass eine Menge Q mit einer Produktionsfunktion F produziert wird, die abhängig ist von den beiden Inputs K und L.
Beispiel: Ein Unternehmen produziert mit einer Produktionsfunktion von $F(K,L)=KL$. Mit einem Kapitaleinsatz von 5 und 2 Einheiten von L, kann das Unternehmen 10 Einheiten produzieren.

Durchschnittsprodukt und Grenzprodukt

In der Analyse wie groß die Produktionsmenge pro Einheit eines bestimmten Inputfaktors durchschnittlich ist, muss die Produktionsmenge durch die Inputmenge geteilt werden. Werden mit 5 Arbeitern 50 Einheiten produziert, so produziert jeder Arbeiter im Durchschnitt 10 Einheiten. Allgemein lässt sich die Produktionsfunktion, die die Produktionsmenge beschreibt, durch die Inputmenge teilen.
Durchschnittsprodukt der Arbeit: $DPL={\frac {F(K,L)}{L}}$
Soll das Durchschnittsprodukt der Arbeit berechnet werden, kann die Produktionsfunktion durch eine allgemeine Menge der Arbeit geteilt werden. Das Ergebnis ist eine Funktion, die das Durchschnittsprodukt für ein allgemeines L angibt. Ist das DPL beispielsweise gleich 10/L, so ist das DPL für 5 Arbeiter 2 und für 2 Arbeiter 5. Es kann auch Fälle geben, für die das Durchschnittsprodukt der Arbeit eine konstante Zahl ist. In dem Fall ist das DPL konstant und unabhängig von L.
Das Durchschnittsprodukt lässt sich für sämtliche Inputfaktoren auf dieselbe Art berechnen und ist aus der Berechnung der durchschnittlichen Kosten bekannt.


Das Grenzprodukt betrachtet um wie viel eine marginale Einheit eines Inputfaktors ceteris paribus die Produktionsmenge verändert. Diese marginale Änderung ist in der Ableitung der Produktionsfunktion nach dem zu betrachtenden Inputfaktor beschrieben. Ist zum Beispiel das Grenzprodukt der Arbeit von Interesse, so wird die Produktionsfunktion nach L abgeleitet
(${\frac {\partial F(K,L)}{\partial L}}$).

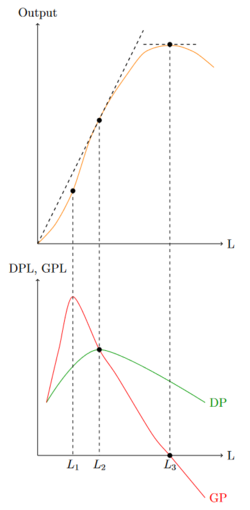
Die Relation zwischen dem Durchschnittsprodukt und dem Grenzprodukt wird in der Abbildung links deutlich. Seien alle Inputfaktoren konstant, verändert ein steigendes Level von L den Output. Ohne Arbeit findet keine Produktion statt und je mehr L eingesetzt wird, desto größer wird anfangs die Produktionsmenge. Dabei steigt die Menge nicht nur, sie steigt auch immer stärker. Jede einzelne Einheit von L erhöht die Produktionsmenge stärker als die Einheit vorher. Das Grenzprodukt ist demnach positiv und steigend. Bei einer Menge $L_{1}$ steigt der Output am stärksten an, das Grenzprodukt hat hier sein Maximum. Nach diesem sinkt das Grenzprodukt und bleibt dabei positiv. Die Produktionsmenge steigt demnach weiter, jedoch sind zusätzliche Einheiten Arbeit weniger effektiv als die vorigen. Sobald das Grenzprodukt negativ wird, reduziert jede weitere Einheit die Produktionsmenge, daher hat die Produktionsfunktion bei $L_{3}$ ein Maximum.
Die Steigung der gestrichelten Linie, die durch den Ursprung und einen Punkt auf der Produktionsfunktion verläuft, stellt das Durchschnittsprodukt für die jeweilige Menge von L dar. Startend bei L=0 steigt das Durchschnittsprodukt, ehe es nach $L_{2}$ wieder anfängt zu sinken. Die DPL-Funktion besitzt bei dieser Menge ein Maximum. Es kann allgemein bewiesen werden, dass die GP-Funktion durch das lokale Maximum verläuft.
${\frac {\partial DPL}{\partial L}}={\frac {\partial [{\frac {F(K,L)}{L}}]}{\partial L}}={\frac {F_{L}(K,L)*L-F(K,L)*1}{L^{2}}}=0$
$F_{L}(K,L)*L-F(K,L)=0$
$F_{L}(K,L)*L=F(K,L)$
$F_{L}(K,L)={\frac {F(K,L)}{L}}$
$GPL=DPL$
Im Extrempunkt des Durchschnittsprodukt ist dieses gleich dem Grenzprodukt.

Isoquante

Die Isoquante gibt alle möglichen Kombinationen der Inputfaktoren an, bei denen die Produktionsmenge konstant bleibt ${\bar {Q}}=F(K,L)$. Zu grafischen Darstellung muss nach einer der beiden Inputfaktoren umgestellt werden. Sei beispielsweise $F(K,L)=K^{0,5}L^{0,5}$ die Produktionsfunktion. Ein konstantes Produktionslevel führt zu
$K={\frac {{\bar {Q}}^{2}}{L}}$
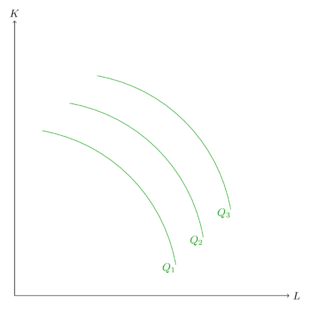
Analog zu den Indifferenzkurven, können die Isoquanten grafisch dargestellt werden.

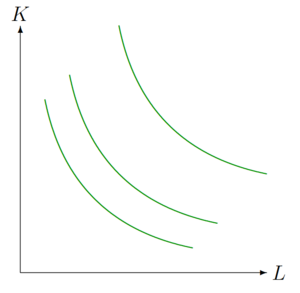
Unbeachtet dessen, dass Isoquanten auch anders verlaufen können, sind die obigen typisch, da sie ein abnehmendes Grenzprodukt implizieren. Ein abnehmendes Grenzprodukt beschreibt das Phänomen, dass der marginale Nutzen einer Einheit bei einem steigen des Inputleveles kleiner wird. Wenn in einer Pizzeria ein Arbeiter anfängt, ist das Grenzprodukt dieses Arbeiters sehr groß. Ein weiterer Arbeiter produziert selbst nicht mehr so viele Pizzen wie der erste, aber immer noch mehr als der dritte. Je mehr Pizzabäcker eingestellt werden, desto kleiner wird das Grenzprodukt. Ist die unterste Isoquante Teil der Betrachtung und in der derzeitigen Güterkombination wird sie mit einem geringen Kapitaleinsatz und sehr hohen Arbeitseinsatz erreicht, benötigt es einen sehr großen zusätzlichen Arbeitseinsatz, um nur eine Einheit des Kapitals einsparen zu können.

Grenzrate der technischen Substitution

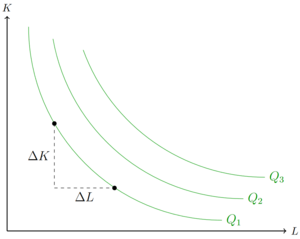
Die Grenzrate der technischen Substitution beschreibt das marginale Austauschverhältnis der beiden Inputs, um das Produktionsniveau beizubehalten (vgl. MRS). Angenommen $\Delta L$ soll eingespart werden. Damit weiterhin $Q_{1}$ erreicht wird benötigt es $\Delta K$. In ein Verhältnis zueinander gesetzt sagt die GRTS aus, wie viele Einheiten von K es benötigt, um eine Einheit von L einzusparen.
$GRTS_{K,L}={\frac {\Delta K}{\Delta L}}$
Eine marginale Sichtweise lässt $\Delta$ gegen null streben. Dafür ergibt sich:
$GRTS_{K,L}={\frac {\frac {\partial F(K,L)}{\partial K}}{\frac {\partial F(K,L)}{\partial L}}}$

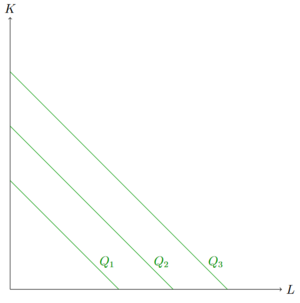
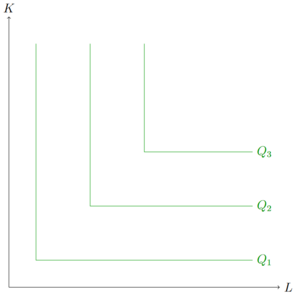
Spezialfälle der Isoquante

Isoquanten können entgegen der Darstellung oben durchaus auch anders verlaufen. Beispiele wären Produktionen, in denen die Inputfaktoren beliebig miteinander substituiert werden können (links). Eine Produktion, bei der die Inputfaktoren nur in einem festen Verhältnis zueinander effizient eingesetzt werden, ist ebenfalls denkbar (mitte), wie eine konkave Indifferenzkurve (rechts).

Die kurze und die lange Frist

In der kurzen Frist kann es vorkommen, dass nicht alle Produktionsfaktoren variabel sind. Es dauert beispielsweise seine Zeit ein weiteres Fabrikgebäude zu bauen. Daher sind einige Inputfaktoren nur langfristig variabel. Diese sind in der kurzen Sichtweise Teil der Fixkosten, während sie in der langen Sicht Teil der variablen Kosten sind. Typischerweise wird in der kurzen Frist angenommen, dass nur die Anzahl an Arbeit (L) verändert werden kann, wo hingegen Kapital (K) fix angenommen wird.

MC Fragen

Die Produktionsfunktion eines Unternehmens beschreibt

	die Menge, die zur Gewinnmaximierung produziert werden sollte
	was technisch machbar ist, wenn das Unternehmen effizient produziert
	den von einem effizient produzierenden Unternehmen erzielten Erlös
	die tatsächliche Produktion des Unternehmens mit gegebenen Inputs
	(alle Antwortmöglichkeiten sind richtig)

Wenn Arbeit der einzig variable Input ist, erreicht das Grenzprodukt sein Maximum

	in dem Punkt, in dem sich die Gesamtproduktkurve nach unten neigt.
	in dem Punkt, in dem die Durchschnittsproduktkurve die Steigung null hat.
	in dem Punkt, in dem sich die Krümmung der Gesamtproduktkurve verändert.
	in dem Punkt, in dem das Durchschnittsprodukt gleich dem Grenzprodukt ist.

Angenommen das Unternehmen Burger Paradise produziert mit folgender Produktionsfunktion: $F(K,L)=ln(L)+{\sqrt {K}}$. Wie lautet die GRTS?

	$GRTS_{L,K}={\frac {ln(L)}{2K}}$
	$GRTS_{K,L}={\frac {2{\sqrt {K}}}{L}}$
	$GRTS_{L,K}={\frac {2{\sqrt {K}}}{L}}$
	$GRTS_{K,L}={\frac {2L}{\sqrt {K}}}$