Skalenerträge

Definition

Skalenerträge geben an, wie sich der Output verändert, wenn alle Produktionsfaktoren mit der gleichen Rate verändert werden. Es wird zwischen abnehmende, konstanten und zunehmenden Skalenerträgen unterschieden. Es besteht ein starker Zusammenhang zwischen den Skalenerträgen und der Frage, ob die Kosten unterproportional, proportional oder überproportional steigen.

Skalenerträge

Skalenerträge schauen sich an in welchem Verhältnis sich der Output verändert, wenn sich alle Produktionsfaktoren mit der gleichen Rate verändern. Werden beispielsweise von allen Produktionsfaktoren das doppelte genutzt geben die Skalenerträge an, wie sich die Produktionsmenge verändert. Wird weniger als das doppelte produziert, liegen abnehmende Skalenerträge vor. Wird genau das doppelte produziert sind die Skalenerträge konstant. Erhöht sich die Produktionsmenge um mehr als das doppelte, sind die Skalenerträge doppelt. In formal allgemeinen Untersuchung wird ein Faktor $\lambda$ genutzt. In dem genannten Beispiel wäre es gleich zwei. Wie verändert sich der Output, wenn $F(\lambda K,\lambda L)$ gilt? Ist es größer, kleiner oder gleich $\lambda *F(K,L)$?
Die Skalenerträge bestimmen, ob Größenvorteile existieren oder nicht. Aussagen können hierüber jedoch nur getroffen werden, wenn auch alle Produktionsfunktionen variabel sind.

Abnehmende Skalenerträge

Die Skalenerträge sind fallend, wenn $F(\lambda K,\lambda L)<\lambda *F(K,L)$ gilt. Grafisch führt eine Verdopplung der Produktionsfaktoren zu einer Isoquante, die ein geringeres Niveau hat als das doppelte der alten Isoquante.


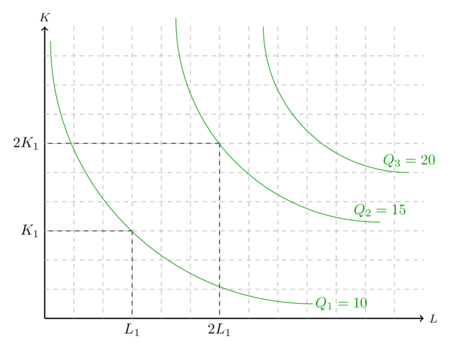
Bei einer Produktionsfunktion mit den beiden Produktionsfaktoren K und L, die oben dargestellte Isoquanten haben, weisen abnehmende Skalenerträge auf. Wenn sowohl K als auch L verdoppelt werden, wird weniger als das doppelte produziert. Anstatt 20 werden lediglich 15 Einheiten erreicht. Um ein Produktionsniveau von 20 zu erreichen wäre mehr als das doppelte des Kapitaleinsatzes nötig.

Konstante Skalenerträge

Die Skalenerträge sind konstant, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(\lambda K,\lambda L)=\lambda*F(K,L) } gilt. Grafisch führt eine Verdopplung der Produktionsfaktoren zu einer Isoquante, die genau das doppelte Produktionsniveau der alten Isoquante darstellt.


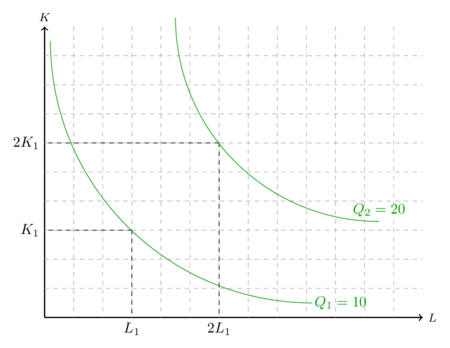
Bei einer Produktionsfunktion mit den beiden Produktionsfaktoren K und L, die oben dargestellte Isoquanten haben, weisen konstante Skalenerträge auf. Wenn sowohl K als auch L verdoppelt werden, wird genau doppelte produziert. Mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L_1 } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_1 } wird 10 Einheiten produziert und mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2*L_1 } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2*K_1 } werden 20 Einheiten produziert.

Zunehmende Skalenerträge

Die Skalenerträge sind steigend, wenn $F(\lambda K,\lambda L)>\lambda *F(K,L)$ gilt. Grafisch führt eine Verdopplung der Produktionsfaktoren zu einer Isoquante, die ein höheres Niveau hat, als das doppelte der alten Isoquante.


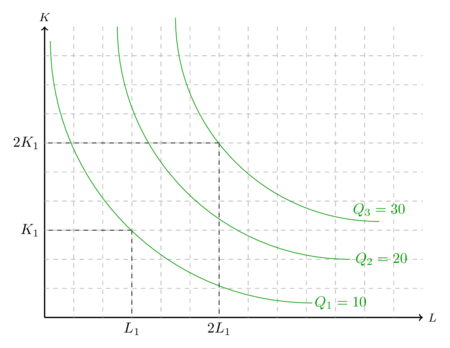
Bei einer Produktionsfunktion mit den beiden Produktionsfaktoren K und L, die oben dargestellte Isoquanten haben, weisen abnehmende Skalenerträge auf. Wenn sowohl K als auch L verdoppelt werden, wird mehr als das doppelte produziert. Anstatt 20 werden sogar 30 Einheiten erreicht. Um ein Produktionsniveau von 20 zu erreichen wäre weniger als das doppelte des Kapitaleinsatzes nötig.

Skalenerträge bei Cobb-Douglas-Produktionsfunktionen

Die Untersuchung von Skalenerträgen bei Cobb-Douglas-Produktionsfunktionen lässt sich allgemein anstellen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(K,L)=K^{\alpha}*L^{\beta} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(\lambda K,\lambda L)=(\lambda*K)^{\alpha}*(\lambda*L)^{\beta} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(\lambda K,\lambda L)=\lambda^{\alpha+\beta}*K^{\alpha}*L^{\beta} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(\lambda K,\lambda L)=\lambda^{\alpha+\beta}*F(K,L) }
Werden die oben erkärten Definition für Abnehmende Skalenerträge, Konstante Skalenerträge und Zunehmende Skalenerträge angewendet, muss analysiert werden in welchem Verhältnis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda^{\alpha+\beta} } und $\lambda$ zueinander stehen. Die Summe aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta } bestimmen welcher der Fälle vorliegt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha+\beta<1 \Rightarrow } Abnehmende Skalenerträge
$\alpha +\beta =1\Rightarrow$ Konstante Skalenerträge
$\alpha +\beta >1\Rightarrow$ Zunehmende Skalenerträge

MC Fragen

Sind die Skaleneträge fallend, konstant oder steigend, wenn die Produktionsfunktion <math> F(K,L)=K^{0,5}+L^{0,5} lautet?

	Die Skalenerträge sind konstant.
	Die Skalenerträge sind fallend.
	Die Skalenerträge sind steigend.

Abnehmende Skalenerträge können aufgrund welcher der folgenden Ursachen auftreten?

	Verdopplung der Anlage und der UAsrüstung zu gleichen Kosten.
	Spezialisierung der Inputs.
	Abnehmendes Grenzprodukt des Kapitals.
	Einsatz von Inputs in ungleichen Verhältnissen.
	Unwirtschaftlichkeiten in der Unternehmensführung.

Ein Produktionsprozess weist zunehmende Skalenerträge auf, wenn...

	... zu einer Verdopplung des Outputs weniger als das Doppelte an Energie benötigt wird.
	... der Output durch die Inbetriebnahme eines zweiten Montagebandes um 100 Prozent gesteigert wird.
	... durch die Hinzufügung einer kompletten zweiten Schicht der Output um weniger als 100 Prozent gesteigert wird.
	... die Produktion durch die Bepflanzung einer doppelt so großen Fläche und die Verdopplung aller anderen Inputs um weniger als 100 Prozent gesteigert wird.