Nash Gleichgewicht: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| Zeile 19: | Zeile 19: | ||
==Nash Gleichgewicht== | ==Nash Gleichgewicht== | ||
| + | ===In reinen Strategien=== | ||
Das Nash Gleichgewicht ist nach John Nash benannte Kombination von Strategien zweier Spieler, bei der kein Spieler einseitig den Anreiz hat abzuweichen. In dem Gefangenendilemma von oben ist das Nash Gleichgewicht NG=(Verrat, Verrat). Spieler 1 hat keinen Anreiz einseitig abzuweichen, wenn er alleine durch seine Entscheidung zu keinem höheren Payoff gelangen kann. Da er nur bestimmten kann in welcher Zeile der Ausgang des Spiels liegen wird, muss geschaut werden, ob er ausgehend von der Entscheidung von Spieler 2 (Verrat) zu einem höheren Payoff gelangen kann. Wählt er statt Verrat doch Schweigen, hat er einen Payoff von -10, was geringer ist als -5. <br> | Das Nash Gleichgewicht ist nach John Nash benannte Kombination von Strategien zweier Spieler, bei der kein Spieler einseitig den Anreiz hat abzuweichen. In dem Gefangenendilemma von oben ist das Nash Gleichgewicht NG=(Verrat, Verrat). Spieler 1 hat keinen Anreiz einseitig abzuweichen, wenn er alleine durch seine Entscheidung zu keinem höheren Payoff gelangen kann. Da er nur bestimmten kann in welcher Zeile der Ausgang des Spiels liegen wird, muss geschaut werden, ob er ausgehend von der Entscheidung von Spieler 2 (Verrat) zu einem höheren Payoff gelangen kann. Wählt er statt Verrat doch Schweigen, hat er einen Payoff von -10, was geringer ist als -5. <br> | ||
| − | Ist ein Ausgang kein Nash Gleichgewicht, wird dieser von rationalen Spielern in der Form nie | + | Ist ein Ausgang kein Nash Gleichgewicht, wird dieser von rationalen Spielern in der Form nie erreicht, da immer ein einseitiger Anreiz zum Abweichen vorliegt. <br> |
Zur Ermittlung des Nash Gleichgewichts soll ein zweites Beispiel dienen. <br> | Zur Ermittlung des Nash Gleichgewichts soll ein zweites Beispiel dienen. <br> | ||
[[Datei:BesteAntwort.png|400px|rahmenlos]] <br clear=all> | [[Datei:BesteAntwort.png|400px|rahmenlos]] <br clear=all> | ||
| Zeile 26: | Zeile 27: | ||
Die [[Spiele#Beste Antwort|Beste Antwort]] ist ein Konzept, bei dem untersucht wird welche Strategie eines Spielers die Beste Antwort auf die Strategie eines anderen Spielers ist. Die Besten Antworten wurden oben mit rot markiert. Die Beste Antwort von Spieler auf die Strategie X ist Strategie 3, da dort der Payoff in der Spalte am größten ist (Zur Erinnerung: Spieler 1 ist der Zeilenspieler und kann bestimmen in welcher Zeile der Ausgang liegen wird). Spieler 2 betrachtet, bei welcher Strategie sein Payoff (der zweitgenannte) in jeder Zeile am größten ist. Wäre der Payoff in mehreren Spalten gleich groß, gibt es mehrere Beste Antworten. <br> | Die [[Spiele#Beste Antwort|Beste Antwort]] ist ein Konzept, bei dem untersucht wird welche Strategie eines Spielers die Beste Antwort auf die Strategie eines anderen Spielers ist. Die Besten Antworten wurden oben mit rot markiert. Die Beste Antwort von Spieler auf die Strategie X ist Strategie 3, da dort der Payoff in der Spalte am größten ist (Zur Erinnerung: Spieler 1 ist der Zeilenspieler und kann bestimmen in welcher Zeile der Ausgang liegen wird). Spieler 2 betrachtet, bei welcher Strategie sein Payoff (der zweitgenannte) in jeder Zeile am größten ist. Wäre der Payoff in mehreren Spalten gleich groß, gibt es mehrere Beste Antworten. <br> | ||
Die Payoffs von (Strategie 1, Strategie X) lauten (3, 3). Ist dies ein Nash Gleichgewicht? Immerhin ist Strategie die Beste Antwort von Spieler 1 auf Strategie X. Tatsächlich hat Spieler 2 in (Strategie 1, Strategie X) einen Anreiz abzuweichen, denn wenn Spieler 1 Strategie 1 wählt, sollte Spieler 2 Strategie Z spielen. (Strategie1, Strategie Z) bietet für Spieler 1 wiederum den Anreiz auf Strategie 2 auszuweichen und so weiter. Nur der Ausgang, der für beide Spieler eine Beste Antwort bedeutet, hat keiner einen Anreiz abzuweichen. Fallen zwei Beste Antworten zusammen, ist der Ausgang ein Nash Gleichgewicht. <br> | Die Payoffs von (Strategie 1, Strategie X) lauten (3, 3). Ist dies ein Nash Gleichgewicht? Immerhin ist Strategie die Beste Antwort von Spieler 1 auf Strategie X. Tatsächlich hat Spieler 2 in (Strategie 1, Strategie X) einen Anreiz abzuweichen, denn wenn Spieler 1 Strategie 1 wählt, sollte Spieler 2 Strategie Z spielen. (Strategie1, Strategie Z) bietet für Spieler 1 wiederum den Anreiz auf Strategie 2 auszuweichen und so weiter. Nur der Ausgang, der für beide Spieler eine Beste Antwort bedeutet, hat keiner einen Anreiz abzuweichen. Fallen zwei Beste Antworten zusammen, ist der Ausgang ein Nash Gleichgewicht. <br> | ||
| − | Mathematisch werden Nash Gleichgewichte | + | ===In gemischten Strategien=== |
| − | <math> (s_1^*,s_2^*) </math> ist ein Nash Gleichgewicht, wenn <math> U_1(s_1^*,s_2^*) \geq U_1(s_i,s_2^*) </math> und <math> U_2(s_1^*,s_2^*) \geq U_2(s_1^*,s_i) </math> für <math> s_i \in S </math>. | + | Ein Spieler sollte seine gemischte Strategie so wählen, dass sein Nutzen maximal ist. Im Beispiel des Schere, Stein, Papier Spiels sollte er die Wahrscheinlichkeiten, mit denen er die jeweiligen reinen Strategien spielt, so wählen, dass der andere Spieler keine dominante Strategie besitzt. Der Nutzen eines Gewinns entspricht 1 und der Nutzen einer Niederlage 0. Die Payoffs ergeben, dass ein rationaler Spieler eine gemischte Strategie <math> σ=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) </math> spielen. Wenn Spieler 1 mit einer größeren Wahrscheinlichkeit Schere spielen würde, müsste Spieler 2 immer Papier spielen, damit sich sein erwarteter Payoff erhöht. Das führt wiederum dazu, dass Spieler 1 einen Anreiz hat abzuweichen. Nur bei <math> σ_1^*=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) </math> und <math> σ_2^*=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) </math> existiert in dem speziellen Anwendungsbeispiel kein Anreiz für einen der beiden Spieler abzuweichen. <math> (σ_1^*,σ_2^*) </math> ist ein Nash Gleichgewicht in gemischten Strategien. <br> |
| + | <br> | ||
| + | Mathematisch werden Nash Gleichgewichte wie folgt definiert: <br> | ||
| + | <math> (s_1^*,s_2^*) </math> ist ein Nash Gleichgewicht, wenn <math> U_1(s_1^*,s_2^*) \geq U_1(s_i,s_2^*) </math> und <math> U_2(s_1^*,s_2^*) \geq U_2(s_1^*,s_i) </math> für <math> s_i \in S </math>. <br> | ||
==IESDS== | ==IESDS== | ||
Version vom 25. August 2023, 13:01 Uhr
Die Normalform ist eine Darstellungsform von Spielen.
Strategien
=Reine Strategien
Ein Spieler hat mehrere Möglichkeiten, wie er in bestimmten Situationen entscheidet. Diese Möglichkeiten werden Strategien gennant. Ein Spieler entscheidet sich für eine Strategie (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s }
) aus allen möglichen Strategien (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S }
). Die mathematische Schreibweise lautet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s \in S }
. Dies bedeutet nichts anderes als dass die gewählte Strategie neben anderen Strategien zur Auswahl stand. Alle möglichen Strategien werden innerhalb einer geschwungenen Klammer dargestellt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=\{s_1,s_2,s_3,...\}}
.
Beispiel: Beim bekannten "Schere Stein Papier" Spiel hat jeder Spieler drei Möglichkeiten, von denen er sich für eine entscheiden muss. Die Spieler wählen beide aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s \in S}
, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=\{Schere,Stein,Papier\}}
.
=Gemischte Strategien
Ein Spieler hat, neben der Möglichkeit sich für eine reine Strategie (entweder Stein oder Papier oder Schere) zu entscheiden, auch die Möglichkeit eine Strategie mit einer bestimmten Wahrscheinlichkeit zu spielen. Das Randomisieren der reinen Strategien wird gemischte Strategie genannt. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle σ=(p_1,p_2,p_3, ...) } ist die Schreibweise von gemischten Strategien. Die erste reine Strategie wird mit einer Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1 } gespielt und so weiter.
Die Normalform
Die Normalform ist eine mögliche Darstellung von Spielen. Die grafische Darstellung ähnelt stark einer Tabelle, in der alle möglichen Strategien des einen Spielers (Spieler 1) an den Anfang jeder Zeile geschrieben werden. Die Strategien des anderen Spielers (Spieler 2) werden in die erste Zeile, an den Anfang jeder Spalte geschrieben.
Als Beispiel soll das sehr bekannte Gefangenendillema dienen. Zwei Verbrecher stehen in unterschiedlichen Räumen unter Verhöhr und werden mit Vorwürden konfrontiert. Man kann ihnen beiden jeweils kleinere Verbrechen nachweisen, die zu einer Haftstrafe von 1 Jahren führen. Ihre möglichen Strategien lauten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=\{Schweigen, Verrat\}}
. Für wie lange sie verurteilt werden hängt davon ab welche Strategie sie selbst wählen und welche Strategie der andere Verbecher wählt. Die folgende Darstellung in Normalform soll die Haftstrafen beschreiben.

Verrät der eine Verbrecher (Spieler 1) den anderen Verbrecher (Spieler 2) und dieser verrät ihn ebenfalls, müssen beide für 5 Jahre. Wählt Spieler 1 Verrat und Spieler 2 Schweigen, bekommt Spieler 1 die Kronzeugenregelung und muss gar nicht ins Gefängnis. Spieler 2 hingegen muss sogar 10 Jahre hinter Gitter. Die anderen Payoffs sind mit einer ähnlichen Inutition zu verstehen.
Nash Gleichgewicht
In reinen Strategien
Das Nash Gleichgewicht ist nach John Nash benannte Kombination von Strategien zweier Spieler, bei der kein Spieler einseitig den Anreiz hat abzuweichen. In dem Gefangenendilemma von oben ist das Nash Gleichgewicht NG=(Verrat, Verrat). Spieler 1 hat keinen Anreiz einseitig abzuweichen, wenn er alleine durch seine Entscheidung zu keinem höheren Payoff gelangen kann. Da er nur bestimmten kann in welcher Zeile der Ausgang des Spiels liegen wird, muss geschaut werden, ob er ausgehend von der Entscheidung von Spieler 2 (Verrat) zu einem höheren Payoff gelangen kann. Wählt er statt Verrat doch Schweigen, hat er einen Payoff von -10, was geringer ist als -5.
Ist ein Ausgang kein Nash Gleichgewicht, wird dieser von rationalen Spielern in der Form nie erreicht, da immer ein einseitiger Anreiz zum Abweichen vorliegt.
Zur Ermittlung des Nash Gleichgewichts soll ein zweites Beispiel dienen.
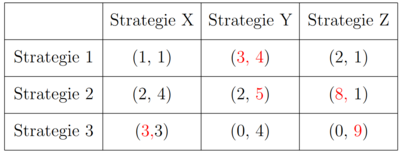
Die Beste Antwort ist ein Konzept, bei dem untersucht wird welche Strategie eines Spielers die Beste Antwort auf die Strategie eines anderen Spielers ist. Die Besten Antworten wurden oben mit rot markiert. Die Beste Antwort von Spieler auf die Strategie X ist Strategie 3, da dort der Payoff in der Spalte am größten ist (Zur Erinnerung: Spieler 1 ist der Zeilenspieler und kann bestimmen in welcher Zeile der Ausgang liegen wird). Spieler 2 betrachtet, bei welcher Strategie sein Payoff (der zweitgenannte) in jeder Zeile am größten ist. Wäre der Payoff in mehreren Spalten gleich groß, gibt es mehrere Beste Antworten.
Die Payoffs von (Strategie 1, Strategie X) lauten (3, 3). Ist dies ein Nash Gleichgewicht? Immerhin ist Strategie die Beste Antwort von Spieler 1 auf Strategie X. Tatsächlich hat Spieler 2 in (Strategie 1, Strategie X) einen Anreiz abzuweichen, denn wenn Spieler 1 Strategie 1 wählt, sollte Spieler 2 Strategie Z spielen. (Strategie1, Strategie Z) bietet für Spieler 1 wiederum den Anreiz auf Strategie 2 auszuweichen und so weiter. Nur der Ausgang, der für beide Spieler eine Beste Antwort bedeutet, hat keiner einen Anreiz abzuweichen. Fallen zwei Beste Antworten zusammen, ist der Ausgang ein Nash Gleichgewicht.
In gemischten Strategien
Ein Spieler sollte seine gemischte Strategie so wählen, dass sein Nutzen maximal ist. Im Beispiel des Schere, Stein, Papier Spiels sollte er die Wahrscheinlichkeiten, mit denen er die jeweiligen reinen Strategien spielt, so wählen, dass der andere Spieler keine dominante Strategie besitzt. Der Nutzen eines Gewinns entspricht 1 und der Nutzen einer Niederlage 0. Die Payoffs ergeben, dass ein rationaler Spieler eine gemischte Strategie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle σ=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) }
spielen. Wenn Spieler 1 mit einer größeren Wahrscheinlichkeit Schere spielen würde, müsste Spieler 2 immer Papier spielen, damit sich sein erwarteter Payoff erhöht. Das führt wiederum dazu, dass Spieler 1 einen Anreiz hat abzuweichen. Nur bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle σ_1^*=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle σ_2^*=(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) }
existiert in dem speziellen Anwendungsbeispiel kein Anreiz für einen der beiden Spieler abzuweichen. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (σ_1^*,σ_2^*) }
ist ein Nash Gleichgewicht in gemischten Strategien.
Mathematisch werden Nash Gleichgewichte wie folgt definiert:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (s_1^*,s_2^*) }
ist ein Nash Gleichgewicht, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_1(s_1^*,s_2^*) \geq U_1(s_i,s_2^*) }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_2(s_1^*,s_2^*) \geq U_2(s_1^*,s_i) }
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_i \in S }
.
IESDS
Das IESDS (Iterated elimination of strictly dominated strategies) ist ein Verfahren, mit dessen Hilfe für Spieler irrationale Strategien eliminiert werden. Ist eine Strategie strikt dominiert, wäre es irrational für einen Spieler diese zu spielen, da mindestens eine Strategie immer einen größeren Payoff liefert.
Eine strikt dominante Strategie kann somit als Strategie gestrichen werden.
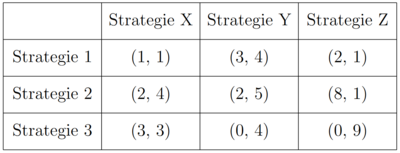
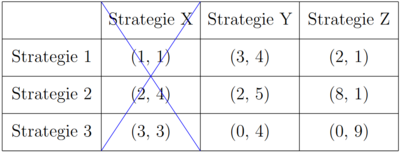
Für Spieler 2 wird die Strategie X von der Strategie Y strikt dominiert (1<4; 4<5; 3<4). Unter der Annahme, dass alle Spieler rational sind, weiß auch Spieler 1, dass Spieler 2 niemals Strategie X wählen wird. Daher muss er die Payoffs in der Strategie X Spalte icht mehr betrachten. Wenn er dies tut, wird seine Strategie 3 von Strategie 2 strikt dominiert (0<2; 0<8). Dass Strategie 3 auch von Strategie 1 strikt dominiert wird, sei an dieser Stelle auch erwähnt. Es ergibt sich eine neue Spielmatrix, da Spieler 1 niemals Strategie 3 wählen wird.
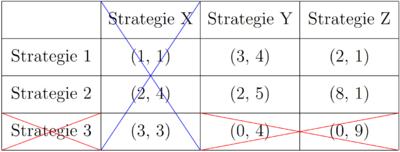
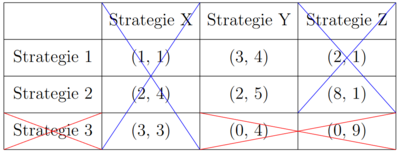
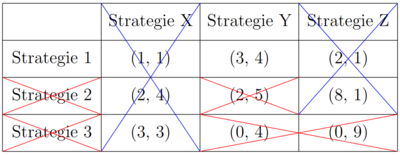
Mit der selben Intution können die restlichen strikt dominierten Strategien eliminiert werden und der einzig rationale Ausgang ist (Strategie 1, Strategie Y). Bleibt nur eine Strategiekombination übrig, bildet sie immer ein Nash Gleichgewicht. Es kann jedoch nicht immer mit der Hilfe des IEDS alle Nash Gleichgewichte gefunden werden.
Nash Gleichgewicht und Pareto Effizienz
Nash Gleichgewichte sind nicht immer parteo effizient. Paretoeffizienz besteht, wenn keine Partei besser gestellt werden kann, ohne die andere schlechter zu stellen. Pareto effiziente Strategiekombinationen lassen sich sehr gut in der Normalform erkennen. Dafür soll wieder das Gefangenendillema vom Anfang dienen

(Schweigen, Verrat) bringt einen Payoff von (-10, 0). Spieler 1 kann sehr leicht besser gestellt werden. SPielt er zum Beispiel auch Verrat, hat er nicht mehr -10, sondern -5. Die Strategiekombination wäre (Verrat, Verrat). Dadurch wird jedoch Spieler 2 schlechter gestellt. Statt 0 hat er nun -5. (Schweigen, Verrat) ist somit eine Strategiekombination, von der aus keine Partei besser gestellt werden kann, ohne eine andere schlechter zu stellen. Es handelt sich um einen pareto effizienten Ausgang. Lediglich (Verrat, Verrat) ist nicht pareto effizient, da in (Schweigen, Schweigen) beide Spieler besser gestellt werden können.
Es ist deutlich geworden, dass der Begriff des Nash Gleichgewichts und der des Pareto Effizienz ganz andere Thematiken abdecken.
Umwandlung in Extensivform
Die Normalform kann in die Extensivform übersetzt werden. Bisher wurde ein statisches Spiel betrachtet. Die Extensivform in der Spielbaumoptik beschreibt aber ohne weitere Modifikation ein sequentielles Spiel. Der Spieler, der weiter oben steht zieht zuerst und danach folgt der andere Spieler. Daher muss etwas eingeführt werden, was verdeutlicht, dass der zweite Spieler nicht weiß, wie sich der erste entschieden hat.

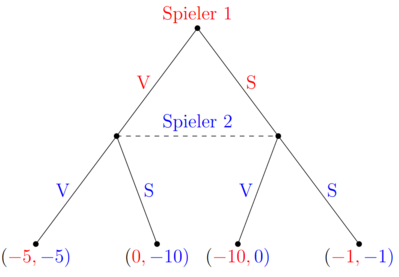
Die gestrichelte Linie siganlisiert, dass Spieler 2 nicht weiß, in welchem Entscheidungsknoten er sich befindet. Die Payoffs selbst verändern sich nicht, nur durch die Übersettzung in die Extensivform. Spielen beide Verrat, erhalten beide auch weiterhin einen Payoff von -5.