Cobb-Douglas-Funktionen

Cobb-Douglas-Funktionen sind Funktionen, die häufig als Nutzenfunktionen oder Produktionsfunktionen genutzt werden.

Aufbau der Cobb-Douglas-Funktionen

Cobb-Douglas-Funktionen haben einen typischen Aufbau, bei dem Variablen multiplikativ miteinander verknüpft sind und einen Exponenten haben.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z(x_1,...,x_n)=b\prod\limits_{i = 0}^{n}x_i^{\alpha_i} } mit $b>0$
Für die Anwendung in der Mikro I genügen zwei Variablen. Zudem kann Parameter $b$ auch den Wert 1 annehmen, sodass sich $z(x_{1},x_{2})=x_{1}^{\alpha }x_{2}^{\beta }$ ergibt. Dies kann dreidimensional dargestellt werden.

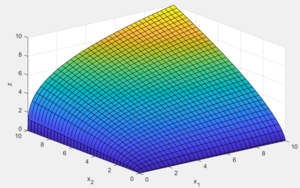
Charakterlich ist vorallem, dass die Variablen $x_{1}$ und $x_{2}$ miteinander multipliziert werden. Nimmt einer der beiden Werte null an, ist der z Wert null.

Skalenerträge

Cobb-Douglas-Produktionsfunktionen haben den Vorteil, dass sie aufgrund ihres Aufbaus leicht auf Skalenerträge untersucht werden können. Für die Untersuchung auf Skalenerträge werden alle Inputfaktoren mit einem allgemeinen Faktor $\lambda$ multipliziert. Sei die Produktionsfunktion beispielsweise $F(K,L)=K^{\alpha }L^{\beta }$, wird hieraus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(\lambda K, \lambda L)=(\lambda K)^{alpha}(\lambda L)^{\beta}=\lambda^{\alpha}K^{\alpha}\lambda^{beta}L^{beta}=\lambda^{\alpha+\beta}K^{\alpha}L^{\beta} } . Dieser Ausdruck wird mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda F(K,L)=\lambda K^{\alpha}L^{beta} } verglichen. Es fällt auf, dass die beiden Ausdrücke identisch sind mit der Ausnahme des Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda^{\alpha+\beta}} Ausdrucks. In dem einen Fall ist der Exponent Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha+\beta } und in dem anderen Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1 } . Ist die Summer der beiden Exponenten größer als 1 gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(\lambda K, \lambda L)>\lambda F(K,L) }
Es gilt:
$\alpha +\beta >1\Rightarrow$ steigende Skalenerträge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha + \beta =1 \Rightarrow } konstante Skalenerträge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha + \beta <1 \Rightarrow } fallende Skalenerträge

Grenzprodukt

Das Grenzrodukt einer Cobb-Douglas-Funktion lässt sich bestimmen, indem die Funktion nach einer der unabhängigen Variablen abgeleitet wird. Zur Veranschaulichung soll eine Cobb-Douglas-Produktionsfunktion dienen, die auf das Grenzprodukt der Arbeit untersucht wird. Die Funktion lautet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(K,L)=K^{\alpha}L^{\beta} }
Das Grenzprodukt der Arbeit lässt sich durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part F(K,L)}{\part K}=\alpha K{\alpha -1}L^{\beta} } berechnen. Das Grenzprodukt ist unter Annahme der nicht negativen Mengen immer dann positiv, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha } positiv, d.h. größer null ist. Das Grenprodukt ist zunehmend oder abnehmend. Das heißt jede weitere Einheit von K bringt entweder mehr oder weniger zusätzlichen Output als die Einheit zuvor. Ist die zweite partielle Ableitung nach K negativ, sinkt die Steigung und es liegt ein abnehmendes Grenzprodukt vor. Bei einer positiven zweiten partellen Ableitung ist das Grenzprodukt zunahmend.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part^2 F(K,L)}{\part^2 K}=\alpha (1-\alpha)K^{\alpha -2}L^{\beta} }
Der Ausdruck oben ist negativ, wenn $\alpha$ kleiner als 1 ist. Die Empirie zeigt, dass das Grenzprodukt häufig positiv und abnehmend ist. Hierfür muss für den Exponent gelten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0<\alpha <1 } .
Die Intuition bei Nutzenfunktionen und dem Grenznutzen ist analog.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part F(.)}{\part x_i}<0 } negatives Grenzprodukt/Grenznutzen

Produktionselastizität

Die Exponenten der Cobb-Douglas Funktionen haben eine Bedeutung und sagen etwas über die dazugehörigen unabhängigen Variablen aus. Dies soll anhand einer Produktionsfunktion gezeigt werden. Hierfür soll untersucht werden, wie sich der Output prozentual verändert, wenn sich einer der beiden Inputfaktoren prozentual verändert. Im ersten Fall soll die Veränderung in K stattfinden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_K=\frac{% \Delta Y}{% \Delta K} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_K=\frac{\Delta Y /Y}{\Delta K / K}=\frac{\Delta Y}{\Delta K}\frac{K}{Y} }
mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta \to 0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_K=\frac{\part Y}{\part K}\frac{K}{Y} }
$\sigma _{K}=\alpha K^{\alpha -1}L^{\beta }{\frac {K}{K^{\alpha }l^{\beta }}}$ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_K=\alpha K^{\alpha -1}L^{\beta}K^{1- \alpha}L^{-\beta} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_K=\alpha K^0L^0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_K=\alpha } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Leftrightarrow } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_L=\beta }

Die Produktionselastizität, also die Frage wie stark sich der Output prozentual verändert, wenn sich einer der Inputfaktoren prozentual verändert lässt sich durch den jeweiligen Exponenten beantworten. Eine ähnliche Intuition gilt bei Cobb-Douglas-Nutzenfunktionen.

Maximum mit Nebenbedingung

Cobb-Douglas-Funktionen haben den Vorteil, dass sich aufgrund ihrer For allgemein eine Lösung für das Haushaltsoptimum bzw. das Produktionsoptimum aufstellen lässt. Hierfür soll eine Cobb Douglas-Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F(x,y)=x^{\alpha}y^{\beta} } mit der Nebenbedingung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_xx+p_y=b } . Zum Maximieren lässt sich die Lagrange Funktion aufstellen, oder es wird direkt die GRS bzw GRTS genutzt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\frac{\part F}{\part x}}{\frac{\part F}{\part y}}=\frac{p_x}{p_y} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\alpha x^{\alpha -1}y^{\beta}}{\beta x^{\alpha}y^{\beta -1}}=\frac{p_x}{p_y} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\alpha}{\beta}\frac{y}{x}=\frac{p_x}{p_y} }
$y={\frac {p_{x}}{p_{y}}}{\frac {\beta }{\alpha }}x$
In die Nebenbedinung eingesetzt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_xx+p_y(\frac{p_x}{p_y}\frac{\beta}{\alpha}x)=b }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_xx(1+\frac{\beta}{\alpha}=b }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_xx(\frac{\alpha +\beta}{\alpha})=b }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^*=\frac{\alpha}{\alpha +\beta}\frac{E}{p_x} } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Leftrightarrow } Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y^*=\frac{\beta}{\alpha +\beta}\frac{E}{p_y} }