Spiele: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
|||
| (23 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
==Strategien== | ==Strategien== | ||
| − | Ein Spieler hat mehrere Möglichkeiten, wie er in bestimmten Situationen entscheidet. Diese Möglichkeiten werden Strategien | + | ===Reine Strategien=== |
| + | Ein Spieler hat mehrere Möglichkeiten, wie er in bestimmten Situationen entscheidet. Diese Möglichkeiten werden Strategien genannt. Ein Spieler entscheidet sich für eine Strategie (<math> s </math>) aus allen möglichen Strategien (<math> S </math>). Die mathematische Schreibweise lautet <math> s \in S </math>. Dies bedeutet nichts anderes, als dass die gewählte Strategie neben anderen Strategien zur Auswahl stand. Alle möglichen Strategien werden innerhalb einer geschwungenen Klammer dargestellt <math> S=\{s_1,s_2,s_3,...\}</math>. <br> | ||
''Beispiel'': Beim bekannten "Schere Stein Papier" Spiel hat jeder Spieler drei Möglichkeiten, von denen er sich für eine entscheiden muss. Die Spieler wählen beide aus <math> s \in S</math>, wobei <math> S=\{Schere,Stein,Papier\}</math>. | ''Beispiel'': Beim bekannten "Schere Stein Papier" Spiel hat jeder Spieler drei Möglichkeiten, von denen er sich für eine entscheiden muss. Die Spieler wählen beide aus <math> s \in S</math>, wobei <math> S=\{Schere,Stein,Papier\}</math>. | ||
| + | |||
| + | ===Gemischte Strategien=== | ||
| + | Ein Spieler hat, neben der Möglichkeit sich für eine reine Strategie (entweder Stein oder Papier oder Schere) zu entscheiden, auch die Möglichkeit eine Strategie mit einer bestimmten Wahrscheinlichkeit zu spielen. Das Randomisieren der reinen Strategien wird gemischte Strategie genannt. <math> \sigma=(p_1,p_2,p_3, ...) </math> ist die Schreibweise von gemischten Strategien. Die erste reine Strategie wird mit einer Wahrscheinlichkeit <math> p_1 </math> gespielt und so weiter. | ||
==Statische und Sequentielle Spiele== | ==Statische und Sequentielle Spiele== | ||
===Statische Spiele=== | ===Statische Spiele=== | ||
| − | Statische Spiele sind Spiele, bei denen die Spieler ihre Strategie gleichzeitig wählen. Ein Beispiel für ein statisches Spiel ist Schere/Stein/Papier. Beide Spieler müssen sich gleichzeitig für eine Strategie entscheiden. Sie können | + | Statische Spiele sind Spiele, bei denen die Spieler ihre Strategie gleichzeitig wählen. Ein Beispiel für ein statisches Spiel ist Schere/Stein/Papier. Beide Spieler müssen sich gleichzeitig für eine Strategie entscheiden. Sie können dementsprechend nicht beobachten, wie der andere Spieler agiert, bzw. für welche Strategie sich der andere Spieler entscheidet. In anderen Fällen treffen die Spieler ihre Entscheidungen nicht gleichzeitig, können aber dennoch nicht beobachten, wie der andere Spieler handelt. Schreibt beispielsweise erst Spieler 1 seine gewählte Strategie auf einen Zettel, lässt diesen zugedeckt und erst dann entscheidet sich Spieler 2, ist dies dennoch ein statisches Spiel. |
===Sequentielle Spiele=== | ===Sequentielle Spiele=== | ||
| − | + | Sequenzielle Spiele (auch dynamische Spiele) sind Spiele, bei denen die Spieler aufeinanderfolgend ihre Strategie spielen. Ein Spieler beginnt und ein zweiter Spieler zieht nach. Der große Unterschied zu den statischen Spielen liegt darin, dass die Spieler die Handlungen der anderen Spieler beobachten können. Schach ist beispielsweise ein sequenzielles Spiel. Der Spieler mit den weißen Figuren (Spieler 1) macht den ersten Zug und der Spieler mit den schwarzen Figuren (Spieler 2) kann den Zug beobachten. Daraufhin zieht er seinen Zug, den wiederum Spieler 1 beobachten kann usw. | |
| − | ==Normalform | + | ==Normalform== |
| − | + | Die Normalform ist eine mögliche Darstellung von Spielen. Die grafische Darstellung ist eine Tabelle, in der alle möglichen Strategien des einen Spielers (Spieler 1) an den Anfang jeder Zeile geschrieben werden. Die Strategien des anderen Spielers (Spieler 2) werden in die erste Zeile, an den Anfang jeder Spalte geschrieben. <br> | |
| − | = | + | Als Beispiel soll das sehr bekannte Gefangenendillemma dienen. Zwei Verbrecher stehen in unterschiedlichen Räumen unter Verhör und werden mit Vorwürfen konfrontiert. Man kann ihnen beiden jeweils kleinere Verbrechen nachweisen, die zu einer Haftstrafe von 1 Jahren führen. Ihre möglichen Strategien lauten <math> S=\{Schweigen, Verrat\}</math>. Für wie lange sie verurteilt werden, hängt davon ab welche Strategie sie selbst wählen und welche Strategie der andere Verbrecher wählt. Die folgende Darstellung in Normalform soll die Haftstrafen beschreiben. <br> |
[[Datei:Gefangenendilemma.png|401px|rahmenlos]] <br> | [[Datei:Gefangenendilemma.png|401px|rahmenlos]] <br> | ||
<br clear=all> | <br clear=all> | ||
| − | + | Verrät der eine Verbrecher (Spieler 1) den anderen Verbrecher (Spieler 2) und dieser verrät ihn ebenfalls, müssen beide für 5 Jahre. Wählt Spieler 1 Verrat und Spieler 2 Schweigen, bekommt Spieler 1 die Kronzeugenregelung und muss gar nicht ins Gefängnis. Spieler 2 hingegen muss sogar 10 Jahre hinter Gitter. Die anderen Payoffs sind mit einer ähnlichen Intuition zu verstehen. <br> | |
| − | + | <br> | |
| − | + | '''Umwandlung in Extensivform''' <br> | |
| − | + | Die Normalform kann in die [[Extensivform]] übersetzt werden. Bisher wurde ein statisches Spiel betrachtet. Die Extensivform in der Spielbaumoptik beschreibt aber ohne weitere Modifikation ein sequenzielles Spiel. Der Spieler, der weiter oben steht, zieht zuerst und danach folgt der andere Spieler. Daher muss etwas eingeführt werden, was verdeutlicht, dass der zweite Spieler nicht weiß, wie sich der erste entschieden hat. <br> | |
| + | [[Datei:Gefangenendilemma.png|401px|rahmenlos]] | ||
| + | [[Datei:NormalInExtensiv.png|399px|rahmenlos]] | ||
| + | <br> | ||
| + | <br clear=all> | ||
| + | Die gestrichelte Linie signalisiert, dass Spieler 2 nicht weiß, in welchem Entscheidungsknoten er sich befindet. Die Payoffs selbst verändern sich nicht, nur durch die Übersetzung in die Extensivform. Spielen beide Verrat, erhalten beide auch weiterhin einen Payoff von -5. | ||
| + | ==Extensivform== | ||
| + | Die [[Extensivform]] eines Spiels ist auch als Spielbaum bekannt. In jedem Knotenpunkt trifft ein Spieler eine Entscheidung. Ein Spieler trifft seine Wahl, die in einen der möglichen Punkte eine Stufe tiefer endet. In diesem Punkt trifft der zweite Spieler seine Entscheidung, die wiederum erneut in einen Entscheidungsknoten mündet. In dem unten grafisch dargestellten Beispiel hat jeder Spieler nur eine Entscheidung zu treffen, weshalb nach der Entscheidung von Spieler 2 die Payoffs feststehen. Der erstgenannte Payoff ist der des ersten Spielers und der Zweite der des Spieler 2. Soll ein statisches Spiel in der Extensivform dargestellt werden, muss grafisch dargestellt werden, dass Spieler 2 in seinen Entscheidungsknoten nicht weiß, wie sich der Spieler 1 entscheidet. Grafisch werden die Entscheidungsknoten des Spielers 2 durch eine gestrichelte Linie miteinander verbunden. Ein Beispiel ist in [[Spiele#Normalform#Umwandlung in Extensivform|Umwandlung in Extensivform]] zu sehen. <br> | ||
[[Datei:Extensivform.png|400px|rahmenlos]] <br> | [[Datei:Extensivform.png|400px|rahmenlos]] <br> | ||
| − | <br | + | <br> |
| − | Die [[ | + | '''Umwandlung in Normalform''' <br> |
| − | + | Die Extensivform kann in die [[Normalform]] umgewandelt werden. Hierfür müssen alle reinen Strategien in die bekannte Matrix geschrieben werden. Spieler 1 hat lediglich die Strategien <math> S_1=\{A, B\} </math>. Die Strategien von Spieler 2 sind aufgrund der sequentiellen Form des Spiels anders als bei simultanen Spielen. Die Strategien bestehen aus allen möglichen Antworten auf eine der Strategien von Spieler 1. Spieler 2 hat beispielsweise die Möglichkeit immer C zu spielen. Er hat aber auch die Möglichkeit nur C zu spielen, wenn er A von Spieler 1 beobachtet und sonst D. Alle möglichen Kombinationen von Spieler 2 lauten <math> S_2=\{CC, CD, DC, DD\} </math> <br> | |
| + | Die Payoffs lassen sich in der Extensivform ablesen. Für Spieler 2 ist entscheiden, ob der Spieler 1 A oder B spielt. Spielt Spieler 1 A, ist der erste Buchstabe von Spieler 2's Strategie relevant, spielt Spieler 2 B, der zweite Buchstabe. Muss beispielsweise der Payoff von (A, CD) ermittelt werden, kann der Spielbaum von oben entsprechend verfolgt werden. Spieler 1 wählt A, deshalb spielt Spieler 2 C. Der Payoff lautet (2, 2). <br> | ||
| + | Es ergibt sich: <br> | ||
| + | [[Datei:TSP2.png|500px|rahmenlos]] | ||
| + | [[Datei:ExtensivinNormal.png|500px|rahmenlos]] | ||
| − | == | + | ==MC Fragen== |
| − | + | <quiz display=simple shuffleanswers=true> | |
| + | {Wählen Sie alle Spiele aus, die statisch sind | ||
| + | |type="[]"} | ||
| + | + Lotto | ||
| + | - Mensch Ärgere Dich Nicht | ||
| + | - 4 gewinnt | ||
| + | + Roulette | ||
| + | </quiz> | ||
| − | == | + | <quiz display=simple shuffleanswers=true> |
| − | + | {Wie lautet das teilspielperfekte Nash-Gleichgewicht des folgenden Spiels? <br> | |
| − | [[Datei: | + | [[Datei:ExtensivMC.png|500px|rahmenlos]] |
| − | + | |type="()"} | |
| − | + | + (A, DD) | |
| − | + | - (A, CC) | |
| + | - (B, DD) | ||
| + | - (B, CC) | ||
| + | - (A, CD) | ||
| + | - (B, DC) | ||
| + | </quiz> | ||
| − | == | + | <quiz display=simple shuffleanswers=true> |
| + | {Welches Nash Gleichgewicht aus dem sequentiellen Spiel oben ist nicht teilspielperfekt? | ||
| + | |type="()"} | ||
| + | + (B, CD) | ||
| + | - (A, CD) | ||
| + | - (A, DD) | ||
| + | - (A, DC) | ||
| + | - (B, DC) | ||
| + | - (B, DD) | ||
| + | </quiz> | ||
Aktuelle Version vom 22. September 2023, 19:45 Uhr
Definition
Ein Spiel ist eine Situation, in der Spieler (Teilnehmer) strategische Entscheidungen treffen, die die Handlungen und Reaktionen der Mitspieler mit einbezieht.
Strategien
Reine Strategien
Ein Spieler hat mehrere Möglichkeiten, wie er in bestimmten Situationen entscheidet. Diese Möglichkeiten werden Strategien genannt. Ein Spieler entscheidet sich für eine Strategie (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s }
) aus allen möglichen Strategien (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S }
). Die mathematische Schreibweise lautet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s \in S }
. Dies bedeutet nichts anderes, als dass die gewählte Strategie neben anderen Strategien zur Auswahl stand. Alle möglichen Strategien werden innerhalb einer geschwungenen Klammer dargestellt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=\{s_1,s_2,s_3,...\}}
.
Beispiel: Beim bekannten "Schere Stein Papier" Spiel hat jeder Spieler drei Möglichkeiten, von denen er sich für eine entscheiden muss. Die Spieler wählen beide aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s \in S}
, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=\{Schere,Stein,Papier\}}
.
Gemischte Strategien
Ein Spieler hat, neben der Möglichkeit sich für eine reine Strategie (entweder Stein oder Papier oder Schere) zu entscheiden, auch die Möglichkeit eine Strategie mit einer bestimmten Wahrscheinlichkeit zu spielen. Das Randomisieren der reinen Strategien wird gemischte Strategie genannt. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma=(p_1,p_2,p_3, ...) } ist die Schreibweise von gemischten Strategien. Die erste reine Strategie wird mit einer Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1 } gespielt und so weiter.
Statische und Sequentielle Spiele
Statische Spiele
Statische Spiele sind Spiele, bei denen die Spieler ihre Strategie gleichzeitig wählen. Ein Beispiel für ein statisches Spiel ist Schere/Stein/Papier. Beide Spieler müssen sich gleichzeitig für eine Strategie entscheiden. Sie können dementsprechend nicht beobachten, wie der andere Spieler agiert, bzw. für welche Strategie sich der andere Spieler entscheidet. In anderen Fällen treffen die Spieler ihre Entscheidungen nicht gleichzeitig, können aber dennoch nicht beobachten, wie der andere Spieler handelt. Schreibt beispielsweise erst Spieler 1 seine gewählte Strategie auf einen Zettel, lässt diesen zugedeckt und erst dann entscheidet sich Spieler 2, ist dies dennoch ein statisches Spiel.
Sequentielle Spiele
Sequenzielle Spiele (auch dynamische Spiele) sind Spiele, bei denen die Spieler aufeinanderfolgend ihre Strategie spielen. Ein Spieler beginnt und ein zweiter Spieler zieht nach. Der große Unterschied zu den statischen Spielen liegt darin, dass die Spieler die Handlungen der anderen Spieler beobachten können. Schach ist beispielsweise ein sequenzielles Spiel. Der Spieler mit den weißen Figuren (Spieler 1) macht den ersten Zug und der Spieler mit den schwarzen Figuren (Spieler 2) kann den Zug beobachten. Daraufhin zieht er seinen Zug, den wiederum Spieler 1 beobachten kann usw.
Normalform
Die Normalform ist eine mögliche Darstellung von Spielen. Die grafische Darstellung ist eine Tabelle, in der alle möglichen Strategien des einen Spielers (Spieler 1) an den Anfang jeder Zeile geschrieben werden. Die Strategien des anderen Spielers (Spieler 2) werden in die erste Zeile, an den Anfang jeder Spalte geschrieben.
Als Beispiel soll das sehr bekannte Gefangenendillemma dienen. Zwei Verbrecher stehen in unterschiedlichen Räumen unter Verhör und werden mit Vorwürfen konfrontiert. Man kann ihnen beiden jeweils kleinere Verbrechen nachweisen, die zu einer Haftstrafe von 1 Jahren führen. Ihre möglichen Strategien lauten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S=\{Schweigen, Verrat\}}
. Für wie lange sie verurteilt werden, hängt davon ab welche Strategie sie selbst wählen und welche Strategie der andere Verbrecher wählt. Die folgende Darstellung in Normalform soll die Haftstrafen beschreiben.

Verrät der eine Verbrecher (Spieler 1) den anderen Verbrecher (Spieler 2) und dieser verrät ihn ebenfalls, müssen beide für 5 Jahre. Wählt Spieler 1 Verrat und Spieler 2 Schweigen, bekommt Spieler 1 die Kronzeugenregelung und muss gar nicht ins Gefängnis. Spieler 2 hingegen muss sogar 10 Jahre hinter Gitter. Die anderen Payoffs sind mit einer ähnlichen Intuition zu verstehen.
Umwandlung in Extensivform
Die Normalform kann in die Extensivform übersetzt werden. Bisher wurde ein statisches Spiel betrachtet. Die Extensivform in der Spielbaumoptik beschreibt aber ohne weitere Modifikation ein sequenzielles Spiel. Der Spieler, der weiter oben steht, zieht zuerst und danach folgt der andere Spieler. Daher muss etwas eingeführt werden, was verdeutlicht, dass der zweite Spieler nicht weiß, wie sich der erste entschieden hat.

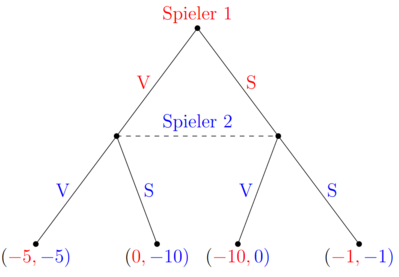
Die gestrichelte Linie signalisiert, dass Spieler 2 nicht weiß, in welchem Entscheidungsknoten er sich befindet. Die Payoffs selbst verändern sich nicht, nur durch die Übersetzung in die Extensivform. Spielen beide Verrat, erhalten beide auch weiterhin einen Payoff von -5.
Extensivform
Die Extensivform eines Spiels ist auch als Spielbaum bekannt. In jedem Knotenpunkt trifft ein Spieler eine Entscheidung. Ein Spieler trifft seine Wahl, die in einen der möglichen Punkte eine Stufe tiefer endet. In diesem Punkt trifft der zweite Spieler seine Entscheidung, die wiederum erneut in einen Entscheidungsknoten mündet. In dem unten grafisch dargestellten Beispiel hat jeder Spieler nur eine Entscheidung zu treffen, weshalb nach der Entscheidung von Spieler 2 die Payoffs feststehen. Der erstgenannte Payoff ist der des ersten Spielers und der Zweite der des Spieler 2. Soll ein statisches Spiel in der Extensivform dargestellt werden, muss grafisch dargestellt werden, dass Spieler 2 in seinen Entscheidungsknoten nicht weiß, wie sich der Spieler 1 entscheidet. Grafisch werden die Entscheidungsknoten des Spielers 2 durch eine gestrichelte Linie miteinander verbunden. Ein Beispiel ist in Umwandlung in Extensivform zu sehen.
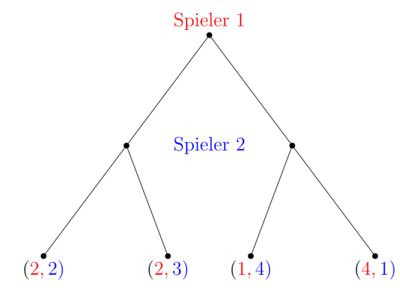
Umwandlung in Normalform
Die Extensivform kann in die Normalform umgewandelt werden. Hierfür müssen alle reinen Strategien in die bekannte Matrix geschrieben werden. Spieler 1 hat lediglich die Strategien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S_1=\{A, B\} }
. Die Strategien von Spieler 2 sind aufgrund der sequentiellen Form des Spiels anders als bei simultanen Spielen. Die Strategien bestehen aus allen möglichen Antworten auf eine der Strategien von Spieler 1. Spieler 2 hat beispielsweise die Möglichkeit immer C zu spielen. Er hat aber auch die Möglichkeit nur C zu spielen, wenn er A von Spieler 1 beobachtet und sonst D. Alle möglichen Kombinationen von Spieler 2 lauten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S_2=\{CC, CD, DC, DD\} }
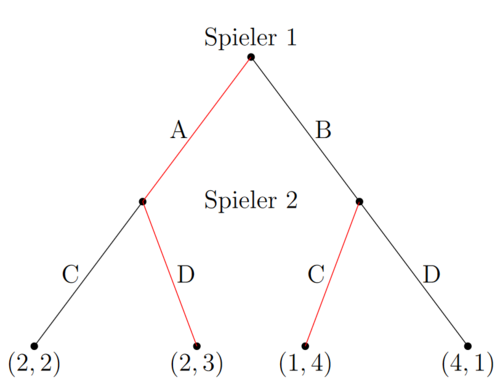
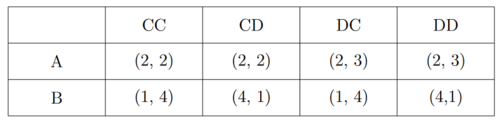
Die Payoffs lassen sich in der Extensivform ablesen. Für Spieler 2 ist entscheiden, ob der Spieler 1 A oder B spielt. Spielt Spieler 1 A, ist der erste Buchstabe von Spieler 2's Strategie relevant, spielt Spieler 2 B, der zweite Buchstabe. Muss beispielsweise der Payoff von (A, CD) ermittelt werden, kann der Spielbaum von oben entsprechend verfolgt werden. Spieler 1 wählt A, deshalb spielt Spieler 2 C. Der Payoff lautet (2, 2).
Es ergibt sich:
MC Fragen