Inputeffizienz, Konsumeffizienz und Outputregel: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
|||
| (35 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Der erste Hauptsatz der | + | Der erste Hauptsatz der Wohlfahrtsökonomie besagt, dass alle Konkurrenzmarktgleichgewichte pareto-effizient sind. Dies kann mittels [[Edgeworth-Box]] für den Handel auf der Konsumentenseite gezeigt werden. Im Weiteren soll gezeigt werden, dass der erste Hauptsatz auch für die Produktion im Wettbewerbsgleichgewicht, den Inputs in Wettbewerbsgleichgewichten, die Allokation der Güter und den Output in Wettbewerbsgleichgewichten gilt. |
__TOC__ | __TOC__ | ||
| − | == | + | ==Konsumeffizienz== |
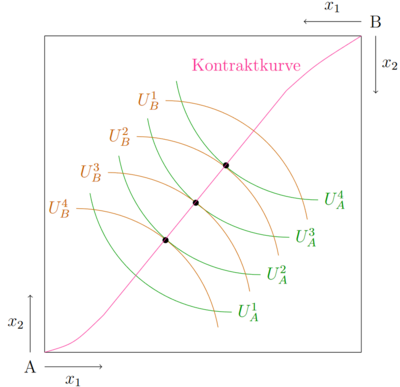
| + | Die [[Edgeworth-Box]] hat gezeigt, dass Konsumenten effizient konsumieren, wenn ihre Grenzrate der Substitution der Grenzrate der Substitution des anderen Konsumenten entspricht. In diesem Punkt kann kein Konsument besser gestellt werden, ohne einen anderen Konsumenten schlechter zu stellen. Alle pareto-effizienten Konsumpunkte liegen auf der Kontraktkurve. Für eine ausführliche Erklärung der Edgeworth-Box, siehe [[Edgeworth-Box|hier]]. <br> | ||
| + | Es gilt: <br> | ||
| + | '''Konsumeffizienz''' <br> | ||
| + | <math> GRS^1_{x_1,x_2}=GRS^2_{x_1,x_2} </math> <br> | ||
| + | <math> GRS^1_{x_1,x_2}=\frac{p_1}{p_2}=GRS^2_{x_1,x_2} </math> <br> | ||
| + | [[Datei:Edgeworthbox4.png|400px|rahmenlos]] | ||
| − | ==Inputeffizienz== | + | ==Effiziente Produktion-Inputeffizienz== |
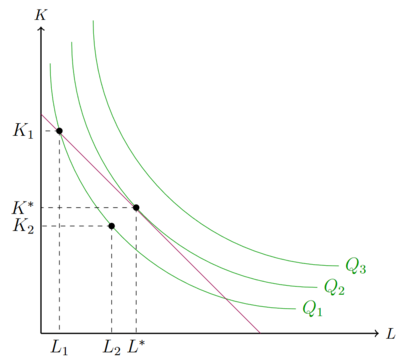
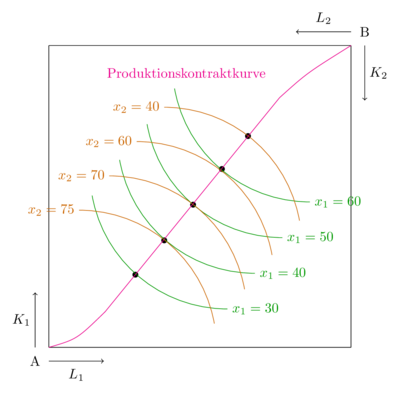
| + | In einer Volkswirtschaft versuchen Unternehmen effizient zu produzieren. Sie produzieren mit möglichst geringen Kosten möglichst viel. Die Berechnung des [[Produktionsoptimum|Produktionsoptimums]] zeigt, dass die Steigung der Isoquante im Optimum dem Preisverhältnis der Inputfaktoren entspricht. Dies kann rechnerisch und auch grafisch, wie in der Abbildung unten links, gezeigt werden. In einer Volkswirtschaft sind die Inputfaktoren häufig begrenzt. Es existieren beispielsweise nicht unendlich viele Menschen in Deutschland, die in der deutschen Wirtschaft arbeiten können. Arbeiten Menschen in Vollzeit für ein Unternehmen 1, können diese nicht mehr Vollzeit für Unternehmen 2 arbeiten. Ähnlich zur [[Edgeworth-Box]] sind auch hier Güter, oder in diesem Fall die Inputfaktoren, begrenzt. In einem Modell mit zwei Unternehmen, die unterschiedliche Produkte herstellen, können sich die Unternehmen die Inputfaktoren in gewisser Weise zuteilen. Wenn es 30 Einheiten Arbeit (L) gibt und Unternehmen 1 20 einsetzt, kann Unternehmen 2 nur noch 10 einsetzen. Das gleiche gilt auch für den Kapitaleinsatz. Dies kann durch eine Ausstattungsbox grafisch dargestellt werden, die starke Ähnlichkeiten zu der [[Edgeworth-Box]] aufweist. Die Ausstattungsbox mitsamt Isoquanten ist in der rechten Abbildung zu sehen. Die Produktionsmenge der beiden Unternehmen steht in einem negativen Verhältnis zueinander. Produziert Unternehmen A viel von Gut <math> x_1 </math>, benötigt es eine große Menge der Inputfaktoren und Unternehmen B kann nur noch eine geringe Menge von Gut <math> x_2 </math> produzieren. Grafisch und rechnerisch zeigt sich, dass die [[Produktionsfunktion und Isoquante#Grenzrate der technischen Substitution|Grenzrate der technischen Substitution (GRTS)]] der beiden Unternehmen im effizienten Gleichgewicht identisch ist. <br> | ||
| + | Die Herleitung ist wie bei der [[Edgeworth-Box]]. <br> | ||
| + | '''Inputeffizienz''' <br> | ||
| + | <math> GRTS^A_{L,K}=GRTS^B_{L,K} </math> <br> | ||
| + | <math> GRTS^A_{L,K}=\frac{w}{r}=GRTS^B_{L,K} </math> <br> | ||
| + | [[Datei:Produktionsoptimum.png|400px|rahmenlos]] | ||
| + | [[Datei:Ausstattungsbox.png|400px|rahmenlos]] | ||
| − | ==Effiziente Allokation der Güter== | + | ==Effiziente Allokation der Güter-Outputregel== |
| − | + | [[Datei:Transformationskurve1.png|350px|links]] | |
| − | <math> | + | Die Herleitungen der [[Inputeffizienz, Konsumeffizienz und Outputregel#Effiziente Produktion-Inputeffizienz|effizienten Produktion/Inputeffizienz]] zeigt, dass eine Volkswirtschaft in diesem Modell vor dem Trade-off zwischen der Produktion von Gut <math> x_1 </math> und der Produktion von Gut <math> x_2 </math> steht. Soll viel von dem Gut <math> x_1 </math> produziert werden, kann weniger von Gut <math> x_2 </math> produziert werden. Die beiden Güter stehen in einem Austauschverhältnis zueinander, dass verschiedene Werte annehmen kann. Das Verhältnis kann beispielsweise linear sein. In diesem Fall kann für jedes Gut <math> x_1 </math> weniger immer eine konstant bleibende Menge <math> x_2 </math> mehr produziert werden. Es sind auch Austauschverhältnisse möglich, die nicht linear sind. In diesem Fall hängt die zusätzliche Menge, die von Gut <math> x_2 </math> produziert werden kann, immer mit der Menge von <math> x_2 </math> zusammen, die bereits produziert wird. Dieses Phänomen hat starke Bezüge zum abnehmenden [[Marginale Sichtweise#Grenznutzen|Grenznutzen]]. Hier stiftet eine zusätzliche Einheit einen immer kleiner werdenden Nutzen, je mehr von diesem Gut bereits konsumiert wird. Im Kontext der Produktion bedeutet dies, dass immer weniger von einem Gut <math> x_2 </math> durch ein eingespartes Gut <math> x_1 </math> produziert werden kann, je mehr von diesem Gut bereits produziert wird. Ein solcher Fall ist in der Abbildung links dargestellt. Die [[Inputeffizienz, Konsumeffizienz und Outputregel#Effiziente Produktion|effizienten Produktion]] hat in dem Beispiel gezeigt, dass wenn von <math> x_1 </math> 40 Einheiten produziert werden, von <math> x_2 </math> effizient 75 Einheiten produziert werden können. Sollen von <math> x_1 </math> 20 Einheiten produziert werden, können von <math> x_2 </math> nur 70 Einheiten produziert werden. Das selbe Prinzip gilt für <math> x_1=50 </math> und <math> y_1=60 </math>. Die jeweiligen Kombinationen von <math> x_1-x_2 </math> können in ein entsprechendes Diagramm eingezeichnet werden. Dies wurde in dem Beispiel unter der Ausstattungsbox getan. Die Verbindungslinie aller effizienten Produktionsmengen ist die Transformationskurve. Die Transformationskurve hat eine negative Steigung und gibt in jedem einzelnen Punkt an, in welchen Verhältnis <math> x_1 </math> zu <math> x_2 </math> transformiert werden können. Gegeben einer Funktion kann die Grenzrate der Transformation (GRT), also die Rate der Transformation in der [[Marginale Sichtweise|Grenzbetrachtung]], durch die partielle Ableitung nach <math> x_1 </math> durch die partielle Ableitung nach <math> x_2 </math>. Es kann mathematisch gezeigt werden, dass die GRT dem Grenzkostenverhältnis entspricht. <br> |
| − | + | <math> GRT_{x_1,x_2}=\frac{MC_1}{MC_2}=\frac{GK_1}{GK_2} </math> | |
| − | + | <br> | |
| + | An dieser Stelle sei nochmal erwähnt, dass die Transformationskurve aus den effizienten Produktionsniveaus besteht. Entlang der Transformationskurve existiert demnach immer die Inputeffizienz. <br> | ||
| + | Auf der Transformationskurve gilt überall: <math> GRTS^1_{L,K}=GRTS^2_{L,K} </math> | ||
<br clear=all> | <br clear=all> | ||
| − | + | ||
| − | + | Die Ausführungen oben zeigen, wie zwischen der Produktion zweier Güter gewählt werden kann. Wie einfach der Wechsel von Produktion des Gutes <math> x_2 </math> zu Gut <math> x_1 </math> ist zeigt sich in der GRT. Jedoch stellt sich weiterhin die Frage, welche Aufteilung optimal ist. Recht intuitiv unter den Standardannahmen ist, dass die optimale Menge auf der Transformationskurve liegt. Ein Unternehmen wird so viele Güter wie möglich produzieren und damit verkaufen wollen. Dass es jedoch auch für die Konsumenten in einer gesellschaftlichen Sichtweise optimal ist, wenn das Unternehmen auf der Transformationskurve produziert, zeigt die weitere Ausführung. Hierfür sollen Indifferenzkurven aus gesellschaftlicher Sicht modelliert werden. Unter den [[Axiome der Nutzentheorie|Annahmen über Präferenzen]] ist eine hohe Konsummenge besser als eine leicht geringere. Die Gesellschaft versucht also als Ganzes auf eine möglichst hohe [[Präferenzen und Indifferenzkurven#Indifferenzkurven|Indifferenzkurve]] zu gelangen. Diese liegt im Tangentialpunkt der Indifferenzkurve mit der Transformationskurve, der in der Abbildung unten eingezeichnet ist. Es muss also gelten <br> | |
| − | |||
| − | Die Ausführungen oben zeigen, wie | ||
<math> GRT=GRS </math> <br> | <math> GRT=GRS </math> <br> | ||
| + | Die vorherigen Ausführungen haben gezeigt, dass <math> GRT_{x_1,x_2}=\frac{GK_1}{GK_2} </math> und <math> GRS_{x_1,x_2}=\frac{p_1}{p_2} </math> bei einem effizienten Output gilt also: <br> | ||
| + | '''Outputregel''' <br> | ||
| + | <math> GRT_{x_1,x_2}=GRS_{x_1,x_2} </math> | ||
| + | <math> GRT_{x_1,x_2}=\frac{GK_1}{GK_2}=\frac{p_1}{p_2}=GRS_{x_1,x_2} </math> <br> | ||
| + | Das Preisverhältnis der beiden Güter muss gleich dem Grenzkostenverhältnis sein. Dies ergibt gerade im Kontext des [[Marktformen#Perfekter Wettbewerb|perfekten Wettbewerbs]] Sinn, in dem der Preis eines Gutes gleich seinen Grenzkosten ist. | ||
[[Datei:Allokation.png|400px|rahmenlos]] | [[Datei:Allokation.png|400px|rahmenlos]] | ||
| − | == | + | ==MC Fragen== |
| + | <quiz display=simple shuffleanswers=true> | ||
| + | {Im Rahmen der allgemeinen Gleichgewichtstheorie bezeichnet die Kontraktkurve die Allokation von Gütern... | ||
| + | |type="()"} | ||
| + | + ...bei welchen niemand besser gestellt werden kann ohne gleichzeitig jemand anderen schlechter zu stellen. | ||
| + | - ...welche stets mit der aktuellsten Produktionstechnologie hergestellt wurden. | ||
| + | - ...die ausschließlich im Rahmen einer Tauschökonomie erreicht werden können. | ||
| + | - ...welche bei einem bestimmten Produktionsprozess den maximal erreichbaren Output bei gegebenem Input abbilden. | ||
| + | </quiz> | ||
| + | |||
| + | <quiz display=simple shuffleanswers=false> | ||
| + | {Welche der Effizienzaussagen ist verletzt, wenn der Output-Preis von Gut 1 gleich dessen Grenzkosten entspricht und der Output-Preis von Gut 2 doppelt so groß ist wie die Grenzkosten von Gut 2? | ||
| + | |type="()"} | ||
| + | - Inputeffizienz | ||
| + | - Konsumeffizienz | ||
| + | + Outputregel | ||
| + | - Keine der Antworten ist richtig. | ||
| + | </quiz> | ||
| − | == | + | <quiz display=simple shuffleanswers=false> |
| + | {Welche der fogenden Aussagen ist unter der Betrachtung der üblichen Annahmen über Nutzen- und Produktionsfunktionen '''falsch'''? | ||
| + | |type="()"} | ||
| + | - Die Allokation von Gütern im Tauschgleichgewicht ist nur dann effzient, wenn die Grenzrate der Substitution jedes Güterpaares für alle Verbraucher identisch ist. | ||
| + | - Inputeffzienz liegt dann vor, wenn die Grenzrate der technischen Substitution von Kapital und Arbeit bei allen Gütern gleich ist. | ||
| + | - Das Faktormarktgleichgewicht zweier mobiler Faktoren bei vollkommenem Wettbewerb ist effzient, da die Faktoren jeweils nach ihren Grenzprodukt entlohnt werden. | ||
| + | + Für eine pareto-optimale Gütermischung muss die Grenzrate der Transformation der Grenzrate der technischen Substitution bei allen Gütern entsprechen. | ||
| + | - Keine der genannten Antworten ist korrekt. | ||
| + | </quiz> | ||
Aktuelle Version vom 22. Februar 2024, 14:41 Uhr
Der erste Hauptsatz der Wohlfahrtsökonomie besagt, dass alle Konkurrenzmarktgleichgewichte pareto-effizient sind. Dies kann mittels Edgeworth-Box für den Handel auf der Konsumentenseite gezeigt werden. Im Weiteren soll gezeigt werden, dass der erste Hauptsatz auch für die Produktion im Wettbewerbsgleichgewicht, den Inputs in Wettbewerbsgleichgewichten, die Allokation der Güter und den Output in Wettbewerbsgleichgewichten gilt.
Konsumeffizienz
Die Edgeworth-Box hat gezeigt, dass Konsumenten effizient konsumieren, wenn ihre Grenzrate der Substitution der Grenzrate der Substitution des anderen Konsumenten entspricht. In diesem Punkt kann kein Konsument besser gestellt werden, ohne einen anderen Konsumenten schlechter zu stellen. Alle pareto-effizienten Konsumpunkte liegen auf der Kontraktkurve. Für eine ausführliche Erklärung der Edgeworth-Box, siehe hier.
Es gilt:
Konsumeffizienz
Effiziente Produktion-Inputeffizienz
In einer Volkswirtschaft versuchen Unternehmen effizient zu produzieren. Sie produzieren mit möglichst geringen Kosten möglichst viel. Die Berechnung des Produktionsoptimums zeigt, dass die Steigung der Isoquante im Optimum dem Preisverhältnis der Inputfaktoren entspricht. Dies kann rechnerisch und auch grafisch, wie in der Abbildung unten links, gezeigt werden. In einer Volkswirtschaft sind die Inputfaktoren häufig begrenzt. Es existieren beispielsweise nicht unendlich viele Menschen in Deutschland, die in der deutschen Wirtschaft arbeiten können. Arbeiten Menschen in Vollzeit für ein Unternehmen 1, können diese nicht mehr Vollzeit für Unternehmen 2 arbeiten. Ähnlich zur Edgeworth-Box sind auch hier Güter, oder in diesem Fall die Inputfaktoren, begrenzt. In einem Modell mit zwei Unternehmen, die unterschiedliche Produkte herstellen, können sich die Unternehmen die Inputfaktoren in gewisser Weise zuteilen. Wenn es 30 Einheiten Arbeit (L) gibt und Unternehmen 1 20 einsetzt, kann Unternehmen 2 nur noch 10 einsetzen. Das gleiche gilt auch für den Kapitaleinsatz. Dies kann durch eine Ausstattungsbox grafisch dargestellt werden, die starke Ähnlichkeiten zu der Edgeworth-Box aufweist. Die Ausstattungsbox mitsamt Isoquanten ist in der rechten Abbildung zu sehen. Die Produktionsmenge der beiden Unternehmen steht in einem negativen Verhältnis zueinander. Produziert Unternehmen A viel von Gut , benötigt es eine große Menge der Inputfaktoren und Unternehmen B kann nur noch eine geringe Menge von Gut produzieren. Grafisch und rechnerisch zeigt sich, dass die Grenzrate der technischen Substitution (GRTS) der beiden Unternehmen im effizienten Gleichgewicht identisch ist.
Die Herleitung ist wie bei der Edgeworth-Box.
Inputeffizienz
Effiziente Allokation der Güter-Outputregel
Die Herleitungen der effizienten Produktion/Inputeffizienz zeigt, dass eine Volkswirtschaft in diesem Modell vor dem Trade-off zwischen der Produktion von Gut und der Produktion von Gut steht. Soll viel von dem Gut produziert werden, kann weniger von Gut produziert werden. Die beiden Güter stehen in einem Austauschverhältnis zueinander, dass verschiedene Werte annehmen kann. Das Verhältnis kann beispielsweise linear sein. In diesem Fall kann für jedes Gut weniger immer eine konstant bleibende Menge mehr produziert werden. Es sind auch Austauschverhältnisse möglich, die nicht linear sind. In diesem Fall hängt die zusätzliche Menge, die von Gut produziert werden kann, immer mit der Menge von zusammen, die bereits produziert wird. Dieses Phänomen hat starke Bezüge zum abnehmenden Grenznutzen. Hier stiftet eine zusätzliche Einheit einen immer kleiner werdenden Nutzen, je mehr von diesem Gut bereits konsumiert wird. Im Kontext der Produktion bedeutet dies, dass immer weniger von einem Gut durch ein eingespartes Gut produziert werden kann, je mehr von diesem Gut bereits produziert wird. Ein solcher Fall ist in der Abbildung links dargestellt. Die effizienten Produktion hat in dem Beispiel gezeigt, dass wenn von 40 Einheiten produziert werden, von effizient 75 Einheiten produziert werden können. Sollen von 20 Einheiten produziert werden, können von nur 70 Einheiten produziert werden. Das selbe Prinzip gilt für und . Die jeweiligen Kombinationen von können in ein entsprechendes Diagramm eingezeichnet werden. Dies wurde in dem Beispiel unter der Ausstattungsbox getan. Die Verbindungslinie aller effizienten Produktionsmengen ist die Transformationskurve. Die Transformationskurve hat eine negative Steigung und gibt in jedem einzelnen Punkt an, in welchen Verhältnis zu transformiert werden können. Gegeben einer Funktion kann die Grenzrate der Transformation (GRT), also die Rate der Transformation in der Grenzbetrachtung, durch die partielle Ableitung nach durch die partielle Ableitung nach . Es kann mathematisch gezeigt werden, dass die GRT dem Grenzkostenverhältnis entspricht.
An dieser Stelle sei nochmal erwähnt, dass die Transformationskurve aus den effizienten Produktionsniveaus besteht. Entlang der Transformationskurve existiert demnach immer die Inputeffizienz.
Auf der Transformationskurve gilt überall:
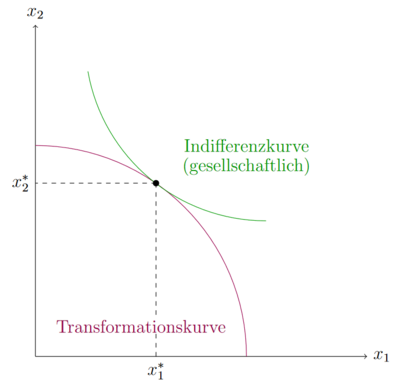
Die Ausführungen oben zeigen, wie zwischen der Produktion zweier Güter gewählt werden kann. Wie einfach der Wechsel von Produktion des Gutes zu Gut ist zeigt sich in der GRT. Jedoch stellt sich weiterhin die Frage, welche Aufteilung optimal ist. Recht intuitiv unter den Standardannahmen ist, dass die optimale Menge auf der Transformationskurve liegt. Ein Unternehmen wird so viele Güter wie möglich produzieren und damit verkaufen wollen. Dass es jedoch auch für die Konsumenten in einer gesellschaftlichen Sichtweise optimal ist, wenn das Unternehmen auf der Transformationskurve produziert, zeigt die weitere Ausführung. Hierfür sollen Indifferenzkurven aus gesellschaftlicher Sicht modelliert werden. Unter den Annahmen über Präferenzen ist eine hohe Konsummenge besser als eine leicht geringere. Die Gesellschaft versucht also als Ganzes auf eine möglichst hohe Indifferenzkurve zu gelangen. Diese liegt im Tangentialpunkt der Indifferenzkurve mit der Transformationskurve, der in der Abbildung unten eingezeichnet ist. Es muss also gelten
Die vorherigen Ausführungen haben gezeigt, dass und bei einem effizienten Output gilt also:
Outputregel
Das Preisverhältnis der beiden Güter muss gleich dem Grenzkostenverhältnis sein. Dies ergibt gerade im Kontext des perfekten Wettbewerbs Sinn, in dem der Preis eines Gutes gleich seinen Grenzkosten ist.
MC Fragen