Haushaltsoptimum: Unterschied zwischen den Versionen
Okehne (Diskussion | Beiträge) |
Okehne (Diskussion | Beiträge) |
||
| (47 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Definition== | ==Definition== | ||
| − | + | Die Konsumgüterbündel eines Konsumenten, das er gegeben seiner Budgetrestriktion am stärksten präferiert, heißt Haushaltsoptimum. Der Nutzen ist in diesem Konsumbündel maximiert und ein höheres Nutzenniveau kann aufgrund der Budgetrestriktion nicht erreicht werden. <br> | |
| + | Sollte eines der Güter ein [[Güter und Ungüter#Ungüter|Ungut/Schlecht]] sein, gilt es dieses im Haushaltsoptimum bei positiven Preisen möglichst nicht zu konsumieren. | ||
__TOC__ | __TOC__ | ||
==Das Haushaltsoptimum grafisch== | ==Das Haushaltsoptimum grafisch== | ||
| − | Das Haushaltsoptimum liegt im Tangentialpunkt der [[Budgetrestriktion und Budgetgerade#Budgetgerade|Budgetgeraden]] und der [[Präferenzen und Indifferenzkurven#Indifferenzkurven|Indifferenzkurve]]. Dies hängt mit den [[Axiome der Nutzentheorie|Axiomen der Nutzentheorie]] zusammen. Aufgrund der [[Axiome der Nutzentheorie|Monotonie/Lokale nicht Sättigung]] ist es für den Konsumenten | + | Das Haushaltsoptimum liegt im Tangentialpunkt der [[Budgetrestriktion und Budgetgerade#Budgetgerade|Budgetgeraden]] und der [[Präferenzen und Indifferenzkurven#Indifferenzkurven|Indifferenzkurve]]. Dies hängt mit den [[Axiome der Nutzentheorie|Axiomen der Nutzentheorie]] zusammen. Aufgrund der [[Axiome der Nutzentheorie|Monotonie/Lokale nicht Sättigung]] ist es für den Konsumenten besser mehr von beiden Gütern zu konsumieren. Deshalb gilt <math> U_1<U_2<U_3 </math>. Der Konsument ist in seinem [[Budgetrestriktion und Budgetgerade#Budgetrestriktion|Budget]] limitiert. Er kann lediglich sein Einkommen E für seinen Konsum ausgeben. Der Konsum unterhalb der Budgetgeraden ist genauso möglich, wie der Konsum auf der Budgetgerade. Der Konsum oberhalb der Budgetgerade ist nicht möglich, da hierfür ein größeres Budget nötig wäre. <br> |
[[Datei:Haushaltsoptimum.png|401px|rahmenlos]] <br> | [[Datei:Haushaltsoptimum.png|401px|rahmenlos]] <br> | ||
<br clear=all> | <br clear=all> | ||
| − | Der nutzenmaximale Punkt kann nicht unterhalb der Budgetgeraden liegen. Befindet sich der aktuelle Konsumpunkt doch unterhalb der Budgetgeraden, erhöht sich der Nutzen, sobald der Konsument von mindestens einem der beiden Gütern mehr konsumiert. Dementsprechend muss im Optimum dieses Modells das gesamte Budget aufgebraucht werden. Wo genau das Optimum auf der | + | Der nutzenmaximale Punkt kann nicht unterhalb der Budgetgeraden liegen. Befindet sich der aktuelle Konsumpunkt doch unterhalb der Budgetgeraden, erhöht sich der Nutzen, sobald der Konsument von mindestens einem der beiden Gütern mehr konsumiert. Dementsprechend muss im Optimum dieses Modells das gesamte Budget aufgebraucht werden. Wo genau das Optimum auf der Budgetgerade liegt, hängt von dem Verlauf der Indifferenzkurven ab. Der Nutzen ist unter den Standardannahmen maximiert, wenn eine Indifferenzkurve die Budgetgerade tangiert. Jede Indifferenzkurve, die die Budgetgerade schneidet, bildet nicht das Maximum ab, da durch eine Änderung im Konsumverhalten ein höheres Nutzenniveau erreicht werden kann. Liegt der momentane Konsumpunkt beispielsweise mit Schnittpunkt der Budgetgeraden und auf der Indifferenzkurve <math> U_1 </math>, kann noch die Indifferenzkurve <math> U_2 </math> erreicht werden. Ausgehend von diesem neuen Punkt ist kein Punkt auf einer höheren Indifferenzkurve (<math> U_3 </math> ) erreichbar. |
| − | ==Das Haushaltsoptimum | + | ==Das Haushaltsoptimum analytisch == |
| − | + | Im Haushaltsoptimum maximiert der Haushalt seinen Nutzen, sprich er maximiert seine Nutzenfunktion unter der Maßgabe, dass seine Budgetgleichung erfüllt ist. Zur Maximierung mit Nebenbedingung dient das [[Lagrange|Lagrangeverfahren]]. Alternativ kann auch die [[Gradientenmethode]] genutzt oder die [[Karush-Kuhn-Tucker (KKT)|Karush-Kuhn-Tucker-Bedingungen]] aufgestellt werden. Jedes Verfahren bringt jedoch dasselbe Ergebnis, vorausgesetzt es existiert eine innere Lösung. Das Lagrangeverfahren bringt im zwei Güter Modell <math> (x_1,x_2) </math> folgende notwendige Bedingungen: <br> | |
| − | <math> \frac{\part U( | + | <math> \frac{\part U(x_1,x_2)}{\part x_1}-\lambda p_1=0 </math> <br> |
| − | <math> \frac{\part U( | + | <math> \frac{\part U(x_1,x_2)}{\part x_2}-\lambda p_2=0 </math> <br> |
| − | <math> | + | <math> p_1x_1+p_2x_2-E=0 </math> <br> |
Nach umstellen der beiden ersten Gleichungen ergibt sich die '''Tangentialbedingung''': <br> | Nach umstellen der beiden ersten Gleichungen ergibt sich die '''Tangentialbedingung''': <br> | ||
| − | <math> \frac{\frac{\part U( | + | <math> \frac{\frac{\part U(x_1,x_2)}{\part x_1}}{\frac{\part U(x_1,x_2)}{\part x_2}}=\frac{p_1}{p_2} </math> <br> |
beziehungsweise <br> | beziehungsweise <br> | ||
| − | <math> \frac{ | + | <math> \frac{MU_{x1}}{MU_{x2}}=GRS_{x_1,x_2}=\frac{p_1}{p_2} </math> <br> |
| − | In der Tangentialbedingung wird erkennbar, dass sie unabhängig von dem Budget E ist. Sie | + | In der Tangentialbedingung wird erkennbar, dass sie unabhängig von dem Budget E ist. Sie gibt ein allgemeines Verhältnis an, dass für die beiden Grenznutzen immer gelten muss. Die Steigung der Indifferenzkurve (die [[Präferenzen und Indifferenzkurven#Die Steigung der Indifferenzkurve bzw. Grenzrate der Substitution|Grenzrate der Substitution]]) entspricht gerade der Steigung der Budgetgeraden (dem relativen Preisverhältnis der beiden Güter). Ist diese Bedingung nicht erfüllt, kann der Haushalt durch Anpassung seines Konsumgüterbündels ein höheres Nutzenniveau erreichen. |
| − | <math> \frac{ | + | |
| − | Der | + | Die Tangentialbedingung umgestellt ergibt auch <br> |
| − | Die Tangentialbedingung nach einem der beiden Güter umgestellt und in die dritte Gleichung eingesetzt ergibt die Nachfrage nach den beiden Gütern in Abhängigkeit von den Preisen und dem Budget. | + | <math> \frac{MU_{x1}}{p_1}=\frac{MU_{x2}}{p_2} </math> <br> |
| + | Der Grenznutzen pro bezahlten Preis der beiden Güter muss also im Optimum gleich sein. Die Tangentialbedingung nach einem der beiden Güter umgestellt und in die dritte Gleichung eingesetzt ergibt die Nachfrage nach den beiden Gütern in Abhängigkeit von den Preisen und dem Budget. <br> | ||
==Tangentialbedingung und Grenznutzen== | ==Tangentialbedingung und Grenznutzen== | ||
| − | Die Tangentialbedingung zeigt, ob ein Konsument optimal konsumiert oder nicht. Wenn die GRS nicht gleich dem Preisverhältnis ist, muss der Konsument sein Konsumverhalten | + | Die Tangentialbedingung zeigt, ob ein Konsument optimal konsumiert oder nicht. Wenn die GRS nicht gleich dem Preisverhältnis ist, muss der Konsument sein Konsumverhalten ändern, damit die Gleichung erfüllt ist. Die Preise sind für den Konsumenten fix (er ist Preisnehmer), daher ist es das Grenznutzenverhältnis das angepasst werden muss. Ist das Preisverhältnis beispielsweise 2 und das Grenznutzenverhältnis nur 1, muss er das Grenznutzenverhältnis erhöhen. Da gilt <br> |
| − | <math> GRS_{ | + | <math> GRS_{x_1,x_2}=\frac{MU_{x1}}{MU_{x2}} </math>, <br> |
| − | + | muss der Grenznutzen von x erhöht und/oder der Grenznutzen von y gesenkt werden. Wie das gelingt, wird aus den folgenden Grafiken deutlich: <br> | |
[[Datei:AbnehmenderGrenznutzen.png|350px|rahmenlos]] | [[Datei:AbnehmenderGrenznutzen.png|350px|rahmenlos]] | ||
[[Datei:MU.png|360px|rahmenlos]] <br> | [[Datei:MU.png|360px|rahmenlos]] <br> | ||
<br clear=all> | <br clear=all> | ||
| − | Ausgehend vom [[Marginale Sichtweise| | + | Ausgehend vom [[Marginale Sichtweise|Grenznutzen]], sinkt der zusätzliche Nutzen, den eine Einheit mehr bringt. Der zusätzliche Nutzen einer zweiten Einheit ist größer als der zusätzliche Nutzen der achten Einheit. Dies ist der Grund, warum die Grenznutzenfunktion (rechte Grafik), fallend ist. Damit der Grenznutzen eines Gutes steigt, muss der Konsument weniger von diesem Gut konsumieren. Gilt <br> |
| − | <math> GRS_{ | + | <math> GRS_{x_1,x_2}<\frac{p_1}{p_2} </math>, <br> |
| − | dann ist der Grenznutzen von | + | dann ist der Grenznutzen von <math> x_1 </math> zu klein und der Grenznutzen von <math> x_2 </math> zu groß. Das Konsumniveau von <math> x_1 </math> muss sinken und das Konsumniveau von <math> x_2 </math> steigt. Gilt die Ungleichung oben, liegt der derzeitige Konsumpunkt rechts vom Tangentialpunkt (ausgehend von einem <math>x_1-x_2</math>-Diagramm). |
==Homogenität der Nachfrage== | ==Homogenität der Nachfrage== | ||
| − | Eine Funktion ist im Grad t homogen, wenn gilt <math> f(\ | + | Eine Funktion ist im Grad t homogen, wenn gilt <math> f(\lambda x)=\lambda ^tf(x) </math>. In der Untersuchung, ob die Nachfrage nach einem Gut x homogen in den einzelnen abhängigen Variablen ist, kann dies auf die Nachfragefunktion angewendet werden. <br> |
| − | Eine Nachfrage ist beispielsweise homogen im Einkommen, wenn <math> | + | Eine Nachfrage ist beispielsweise homogen im Einkommen, wenn <math> x_1(p_1,p_2,\lambda E)=\lambda^tx_1(p_1,p_2,E) </math> gilt. <br> |
| − | ''Beispiel'': Die Nachfrage nach dem Gut | + | ''Beispiel'': Die Nachfrage nach dem Gut <math> x_1 </matH> sei <math> x_1(p_1,p_2,E)=p_2E-p_1E </math>. Zur Überprüfung auf Homogenität im Einkommen wird das Einkommen mit einem Faktor <math> \lambda </math> versehen: <math> x_1(p_1,p_2,\lambda E)=p_2(\lambda E)-p_1(\lambda E)=(p_2E-p_1E)\lambda </math>. Es gilt <math> x_1(p_1,p_2,\lambda E)=\lambda^1x_1(p_1,p_2,E) </math>. Die Nachfrage nach <math> x_1 </math> ist im Grad 1 homogen im Einkommen. |
==Hicks'sche und Marshall'sche Nachfrage== | ==Hicks'sche und Marshall'sche Nachfrage== | ||
| − | Das Verfahren, das | + | Das Verfahren, das in der rechnerischen Optimierung geschildert wurde, ergibt die Marshall'sche Nachfrage. Es ist die nutzenmaximale Nachfrage nach einem Gut, bei gegebenem Einkommen (<math> x^M_1(p_1,p_2,E)</math>). Alternativ lässt sich auch die Kostenfunktion minimieren mit der Nebenbedingung das optimale Nutzenniveau <math> U^* </math> zu erreichen. <br> |
| − | [[Datei:Hicks'scheNachfrage.png| | + | [[Datei:Hicks'scheNachfrage.png|402px|rahmenlos]] <br> |
<br clear=all> | <br clear=all> | ||
| − | Ziel ist den Nutzen | + | Ziel ist es den Nutzen mit einem möglichst minimalen Budget E beizubehalten. Die Budgetgerade muss linear verschoben werden, bis zum einen die Indifferenzkurve <math> U_2 </math> erreicht wird und zum anderen die Budgetgerade möglichst nahe am Ursprung liegt. Es ergibt sich ein Tangentialpunkt, der identisch zu dem aus der Vorgehensweise der Nutzenmaximierung ist. Rechnerisch ist die Vorgehensweise identisch zur Marschall'schen Nachfrage. Die Lagrangefunktion wird aufgestellt mit der Zielfunktion, der Ausgaben für den Konsum der beiden Güter, und der Nebenbedingung, der Nutzenfunktion, die gleich <math> U^* </math> sein muss. Das Maximieren nach <math> x_1 </math> und <math> x_2 </math> ergibt zusammen mit der Nebenbedingung drei notwendige Bedingungen. Nach Aufstellen der Tangentialbedingung und Einsetzen in die Nebenbedingung folgt eine Nachfrage nach beiden Gütern, die abhängig von den Preisen und dem Nutzenniveau <math> U^* </math> ist (<math> x^H_1(p_1,p_2,U^*)</math>. <br> |
Die beiden Nachfragen ergeben ceteris paribus dieselben Werte. Dies wird auch als Dualität verstanden: <br> | Die beiden Nachfragen ergeben ceteris paribus dieselben Werte. Dies wird auch als Dualität verstanden: <br> | ||
| − | <math> | + | <math> x_1(p_1,p_2,U^*)=x_1(p_1,p_2,E(p_1,p_2,U^*)) </math> |
==MC Fragen== | ==MC Fragen== | ||
<quiz display=simple shuffleanswers=true> | <quiz display=simple shuffleanswers=true> | ||
| − | {Angenommen Sigmar erfährt in seinem aktuellen Nutzenniveau von | + | {Angenommen Sigmar erfährt in seinem aktuellen Nutzenniveau von Schokolade einen Grenznutzen von 3 und von Büchern einen Grenznutzen von 5. Angenommen eine Einheit Schokolade kostet 1€ und ein Buch kostet 2€ . Wie könnte Sigmar sein Nutzen erhöhen, wenn er bereits sein Budget vollständig ausgibt? (Sichtweise marginal) |
|type="()"} | |type="()"} | ||
+ Sigmar sollte mehr Schokolade und weniger Bücher konsumieren. | + Sigmar sollte mehr Schokolade und weniger Bücher konsumieren. | ||
| Zeile 68: | Zeile 70: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { Lisa hat ein Budget | + | { Lisa hat ein Budget von 90 und eine Nutzenfunktion <math> U(x,y)=x^2+\frac{1}{2}y^2 </math>. Der Preis für x lautet 2 und y kostet 1 pro Einheit. |
|type="{}"} | |type="{}"} | ||
| − | Wie lautet die nutzenmaximale Nachfrage nach y | + | Wie lautet die nutzenmaximale Nachfrage nach y? { 30 } |
</quiz> | </quiz> | ||
Aktuelle Version vom 4. April 2024, 12:09 Uhr
Definition
Die Konsumgüterbündel eines Konsumenten, das er gegeben seiner Budgetrestriktion am stärksten präferiert, heißt Haushaltsoptimum. Der Nutzen ist in diesem Konsumbündel maximiert und ein höheres Nutzenniveau kann aufgrund der Budgetrestriktion nicht erreicht werden.
Sollte eines der Güter ein Ungut/Schlecht sein, gilt es dieses im Haushaltsoptimum bei positiven Preisen möglichst nicht zu konsumieren.
Das Haushaltsoptimum grafisch
Das Haushaltsoptimum liegt im Tangentialpunkt der Budgetgeraden und der Indifferenzkurve. Dies hängt mit den Axiomen der Nutzentheorie zusammen. Aufgrund der Monotonie/Lokale nicht Sättigung ist es für den Konsumenten besser mehr von beiden Gütern zu konsumieren. Deshalb gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_1<U_2<U_3 }
. Der Konsument ist in seinem Budget limitiert. Er kann lediglich sein Einkommen E für seinen Konsum ausgeben. Der Konsum unterhalb der Budgetgeraden ist genauso möglich, wie der Konsum auf der Budgetgerade. Der Konsum oberhalb der Budgetgerade ist nicht möglich, da hierfür ein größeres Budget nötig wäre.
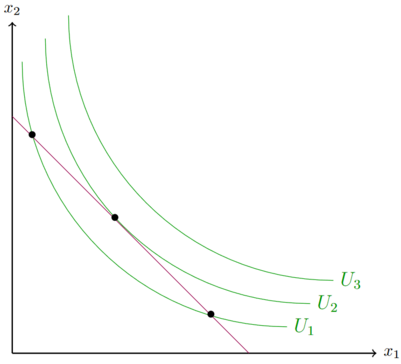
Der nutzenmaximale Punkt kann nicht unterhalb der Budgetgeraden liegen. Befindet sich der aktuelle Konsumpunkt doch unterhalb der Budgetgeraden, erhöht sich der Nutzen, sobald der Konsument von mindestens einem der beiden Gütern mehr konsumiert. Dementsprechend muss im Optimum dieses Modells das gesamte Budget aufgebraucht werden. Wo genau das Optimum auf der Budgetgerade liegt, hängt von dem Verlauf der Indifferenzkurven ab. Der Nutzen ist unter den Standardannahmen maximiert, wenn eine Indifferenzkurve die Budgetgerade tangiert. Jede Indifferenzkurve, die die Budgetgerade schneidet, bildet nicht das Maximum ab, da durch eine Änderung im Konsumverhalten ein höheres Nutzenniveau erreicht werden kann. Liegt der momentane Konsumpunkt beispielsweise mit Schnittpunkt der Budgetgeraden und auf der Indifferenzkurve Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_1 }
, kann noch die Indifferenzkurve Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_2 }
erreicht werden. Ausgehend von diesem neuen Punkt ist kein Punkt auf einer höheren Indifferenzkurve (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_3 }
) erreichbar.
Das Haushaltsoptimum analytisch
Im Haushaltsoptimum maximiert der Haushalt seinen Nutzen, sprich er maximiert seine Nutzenfunktion unter der Maßgabe, dass seine Budgetgleichung erfüllt ist. Zur Maximierung mit Nebenbedingung dient das Lagrangeverfahren. Alternativ kann auch die Gradientenmethode genutzt oder die Karush-Kuhn-Tucker-Bedingungen aufgestellt werden. Jedes Verfahren bringt jedoch dasselbe Ergebnis, vorausgesetzt es existiert eine innere Lösung. Das Lagrangeverfahren bringt im zwei Güter Modell Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (x_1,x_2) }
folgende notwendige Bedingungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part U(x_1,x_2)}{\part x_1}-\lambda p_1=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\part U(x_1,x_2)}{\part x_2}-\lambda p_2=0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1x_1+p_2x_2-E=0 }
Nach umstellen der beiden ersten Gleichungen ergibt sich die Tangentialbedingung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\frac{\part U(x_1,x_2)}{\part x_1}}{\frac{\part U(x_1,x_2)}{\part x_2}}=\frac{p_1}{p_2} }
beziehungsweise
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{MU_{x1}}{MU_{x2}}=GRS_{x_1,x_2}=\frac{p_1}{p_2} }
In der Tangentialbedingung wird erkennbar, dass sie unabhängig von dem Budget E ist. Sie gibt ein allgemeines Verhältnis an, dass für die beiden Grenznutzen immer gelten muss. Die Steigung der Indifferenzkurve (die Grenzrate der Substitution) entspricht gerade der Steigung der Budgetgeraden (dem relativen Preisverhältnis der beiden Güter). Ist diese Bedingung nicht erfüllt, kann der Haushalt durch Anpassung seines Konsumgüterbündels ein höheres Nutzenniveau erreichen.
Die Tangentialbedingung umgestellt ergibt auch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{MU_{x1}}{p_1}=\frac{MU_{x2}}{p_2} }
Der Grenznutzen pro bezahlten Preis der beiden Güter muss also im Optimum gleich sein. Die Tangentialbedingung nach einem der beiden Güter umgestellt und in die dritte Gleichung eingesetzt ergibt die Nachfrage nach den beiden Gütern in Abhängigkeit von den Preisen und dem Budget.
Tangentialbedingung und Grenznutzen
Die Tangentialbedingung zeigt, ob ein Konsument optimal konsumiert oder nicht. Wenn die GRS nicht gleich dem Preisverhältnis ist, muss der Konsument sein Konsumverhalten ändern, damit die Gleichung erfüllt ist. Die Preise sind für den Konsumenten fix (er ist Preisnehmer), daher ist es das Grenznutzenverhältnis das angepasst werden muss. Ist das Preisverhältnis beispielsweise 2 und das Grenznutzenverhältnis nur 1, muss er das Grenznutzenverhältnis erhöhen. Da gilt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GRS_{x_1,x_2}=\frac{MU_{x1}}{MU_{x2}} }
,
muss der Grenznutzen von x erhöht und/oder der Grenznutzen von y gesenkt werden. Wie das gelingt, wird aus den folgenden Grafiken deutlich:
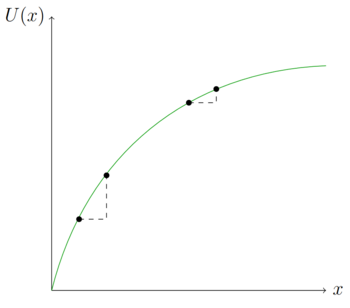
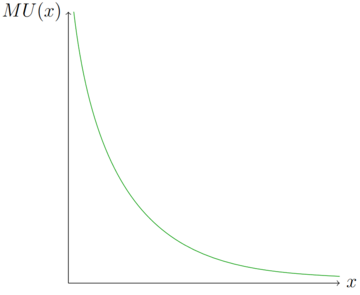
Ausgehend vom Grenznutzen, sinkt der zusätzliche Nutzen, den eine Einheit mehr bringt. Der zusätzliche Nutzen einer zweiten Einheit ist größer als der zusätzliche Nutzen der achten Einheit. Dies ist der Grund, warum die Grenznutzenfunktion (rechte Grafik), fallend ist. Damit der Grenznutzen eines Gutes steigt, muss der Konsument weniger von diesem Gut konsumieren. Gilt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle GRS_{x_1,x_2}<\frac{p_1}{p_2} }
,
dann ist der Grenznutzen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
zu klein und der Grenznutzen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
zu groß. Das Konsumniveau von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
muss sinken und das Konsumniveau von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
steigt. Gilt die Ungleichung oben, liegt der derzeitige Konsumpunkt rechts vom Tangentialpunkt (ausgehend von einem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1-x_2}
-Diagramm).
Homogenität der Nachfrage
Eine Funktion ist im Grad t homogen, wenn gilt . In der Untersuchung, ob die Nachfrage nach einem Gut x homogen in den einzelnen abhängigen Variablen ist, kann dies auf die Nachfragefunktion angewendet werden.
Eine Nachfrage ist beispielsweise homogen im Einkommen, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1(p_1,p_2,\lambda E)=\lambda^tx_1(p_1,p_2,E) }
gilt.
Beispiel: Die Nachfrage nach dem Gut Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1(p_1,p_2,E)=p_2E-p_1E }
. Zur Überprüfung auf Homogenität im Einkommen wird das Einkommen mit einem Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda }
versehen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1(p_1,p_2,\lambda E)=p_2(\lambda E)-p_1(\lambda E)=(p_2E-p_1E)\lambda }
. Es gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1(p_1,p_2,\lambda E)=\lambda^1x_1(p_1,p_2,E) }
. Die Nachfrage nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
ist im Grad 1 homogen im Einkommen.
Hicks'sche und Marshall'sche Nachfrage
Das Verfahren, das in der rechnerischen Optimierung geschildert wurde, ergibt die Marshall'sche Nachfrage. Es ist die nutzenmaximale Nachfrage nach einem Gut, bei gegebenem Einkommen (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^M_1(p_1,p_2,E)}
). Alternativ lässt sich auch die Kostenfunktion minimieren mit der Nebenbedingung das optimale Nutzenniveau Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U^* }
zu erreichen.
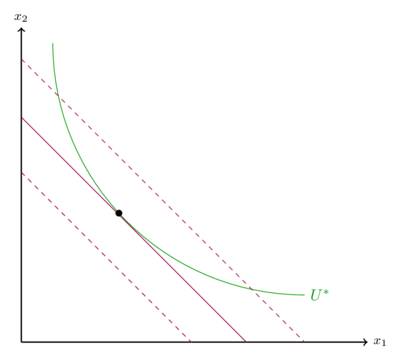
Ziel ist es den Nutzen mit einem möglichst minimalen Budget E beizubehalten. Die Budgetgerade muss linear verschoben werden, bis zum einen die Indifferenzkurve Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_2 }
erreicht wird und zum anderen die Budgetgerade möglichst nahe am Ursprung liegt. Es ergibt sich ein Tangentialpunkt, der identisch zu dem aus der Vorgehensweise der Nutzenmaximierung ist. Rechnerisch ist die Vorgehensweise identisch zur Marschall'schen Nachfrage. Die Lagrangefunktion wird aufgestellt mit der Zielfunktion, der Ausgaben für den Konsum der beiden Güter, und der Nebenbedingung, der Nutzenfunktion, die gleich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U^* }
sein muss. Das Maximieren nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1 }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_2 }
ergibt zusammen mit der Nebenbedingung drei notwendige Bedingungen. Nach Aufstellen der Tangentialbedingung und Einsetzen in die Nebenbedingung folgt eine Nachfrage nach beiden Gütern, die abhängig von den Preisen und dem Nutzenniveau Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U^* }
ist (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^H_1(p_1,p_2,U^*)}
.
Die beiden Nachfragen ergeben ceteris paribus dieselben Werte. Dies wird auch als Dualität verstanden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_1(p_1,p_2,U^*)=x_1(p_1,p_2,E(p_1,p_2,U^*)) }
MC Fragen
