Produktionsoptimum
Das Produktionsoptimum ist der Punkt, in dem ein Unternehmen gegeben einer Produktionsfunktion und Kostenfunktion optimal produziert. Hierbei kann die Produktionsmenge gegeben eines vorhandenen Budgets maximiert oder die Kosten gegeben eines Outputniveaus minimiert werden. Das Unternehmen trifft die Entscheidung wie viel es der jeweiligen Inputs einsetzt.
Produktionsoptimum grafisch
Grafisch liegt das Produktionsoptimum im Tangentialpunkt der Isokostenkurve und der Isoquante. Für ein gegebenes Budget ist die Produktion mit Inputkombinationen, die Kosten unterhalb oder auf der Isokostenkurve erzeugen, zwar möglich führt allerdings nicht zur maximalen Produktionsmenge. Die Produktion oberhalb der Isokostenkurve ist nicht möglich. Bei einer effizienten Technologie bedeutet mehr Input auch mehr Output. Daher gilt . Solange die Isoquante die Isokostenkurve schneidet, ist dieselbe Outputmenge auch mit geringeren Kosten möglich. Erst sobald die Isoquante die Isokostenkurve tangiert, ist die Produktion optimal.
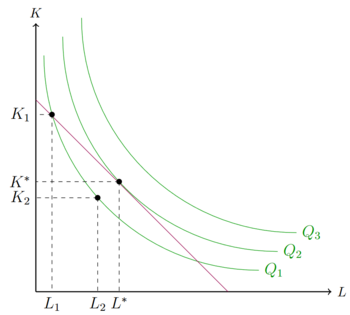
Der Punkt 1 () bringt ein Output von . Der Punkt 2 () bringt ebenfalls , liegt unterhalb der Isokostenkurve und ist somit mit geringeren Kosten verbunden. Nur der Punkt bringt ein Outputniveau, was durch keinen anderen Punkt auf oder unter der Isokostenkurve erreicht werden kann.
Kurze Frist
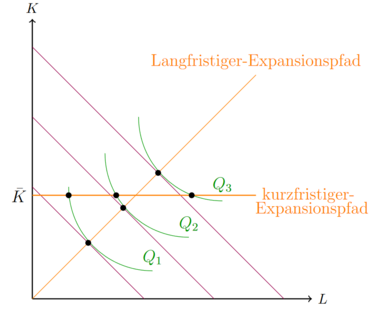
Die Bestimmung des Produktionsoptimums muss in der kurzen Frist und in der langen Frist separat erfolgen. In der kurzen Frist sind häufig ein oder auch mehrere Inputfaktoren nicht variabel. Typischerweise wird in der kurzen Frist davon ausgegangen, das Kapital nicht variabel ist. Das liegt daran, das Produktionshallen oder Maschinen schon erworben wurden. In dem unten skizzierten Beispiel ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K }
in der kurzen Frist nicht variabel. Dementsprechend kann ein Unternehmen auch nur entlang des kurzfristigen Expansionspfades produzieren. Die Schnittpunkte des kurzfristigen Expansionspfades mit den Isoquanten bilden die kurzfristigen Produktionsoptima. Zu beachten ist, dass die eingezeichneten kurzfristigen Optima oberhalb der Isokostenkurve liegen, die die Isoquanten tangieren. Die jeweiligen Produktionsniveaus (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Q_1/Q_2/Q_3}
) bedeuten somit höhere Kosten in der kurzen Frist, als in der langen Frist. Erst in der langen Frist sind alle Produktionsfaktoren variable und die Tangentialpunkte sind erreichbar.
Kostenminimierung
Die Vorgehensweise der Kostenminimierung findet in zwei Schritten statt. Im Ersten Schritt werden für ein allgemeines Outputlevel die optimalen Faktornachfragen gesucht.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \min_{L, K} \, C \, u.d.Nb. \, y=y(K,L) }
Das Ergebnis ist eine optimale Faktornachfrage nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K }
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L }
, die abhängig von den Inputpreisen und dem Produktionsniveau ist. Eingesetzt in die Kostenfunktion ergibt sich eine Kostenfunktion, die nur noch abhängig von den Faktorpreisen (in der Regel konstant) und dem Produktionsniveau ist, .
Im zweiten Schritt wird der Gewinn mit der ausgerechneten Kostenfunktion maximiert.
Der Ansatz wird auch in den MC Fragen bis hierhin beschrieben.
In der obigen Gleichung wird berechnet, bei welchem Outputniveau der Gewinn maximal ist. Das ausgerechnete Produktionsniveau führt eingesetzt in die allgemeinen optimalen Faktornachfragen zu den, in den Graphen oben eingezeichneten und .
Gewinnmaximierung
Die Vorgehensweise der Gewinnmaximierung betrachtet, wann der Umsatz abzüglich der Kosten maximiert ist. Die Gewinnfunktion lautet
Die Gewinnfunktion nach den beiden Variablen K und L differenziert und umgestellt ergeben die optimalen Nachfragen.
MC Frage
Die folgenden Fragen bauen aufeinander auf. Bei falscher Beantwortung wird die richtige Antwort angezeigt.











