Extensivform

Die Extensivform ist eine Darstellungsform von Spielen.

Strategien

Ein Spieler hat mehrere Möglichkeiten, wie er in bestimmten Situationen entscheidet. Diese Möglichkeiten werden Strategien genannt. Ein Spieler entscheidet sich für eine Strategie ($s$) aus allen möglichen Strategien ($S$). Die mathematische Schreibweise lautet $s\in S$. Dies bedeutet nichts anderes, als dass die gewählte Strategie neben anderen Strategien zur Auswahl stand. Alle möglichen Strategien werden innerhalb einer geschwungenen Klammer dargestellt $S=\{s_{1},s_{2},s_{3},...\}$.
Beispiel: Beim bekannten "Schere Stein Papier" Spiel hat jeder Spieler drei Möglichkeiten, von denen er sich für eine entscheiden muss. Die Spieler wählen beide aus $s\in S$, wobei $S=\{Schere,Stein,Papier\}$.

Die Extensivform

Die Extensivform eines Spiels ist auch als Spielbaum bekannt. In jedem Knotenpunkt trifft ein Spieler eine Entscheidung. Ein Spieler trifft seine Wahl, die in einen der möglichen Punkte eine Etage tiefer endet. In diesem Punkt trifft der zweite Spieler seine Entscheidung, die wiederum erneut in einen Entscheidungsknoten mündet. In dem unten grafisch dargestellten Beispiel hat jeder Spieler nur eine Entscheidung zu treffen, weshalb nach der Entscheidung von Spieler 2 die Payoffs feststehen. Der erstgenannte Payoff ist der des Spielers, der angefangen hat und der zweitgenannte der des Nachzüglers.

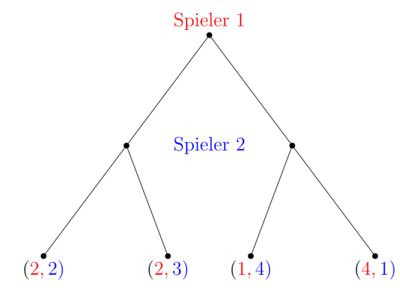
Teilspielperfektheit

Die Teilspielperfektheit ist eine Vereinfachung des Nash Gleichgewichts und untersucht bei Sequentiellen Spielen, welches Resultat rational eintreten wird. Hierbei wird das Konzept der Rückwärtsinduktion eingeführt. Bei der Rückwärtsinduktion wird das sequentielle Spiel rückwärts duchlaufen und untersucht, in welchem Entscheidungspunkt welcher Spieler wie handeln wird.

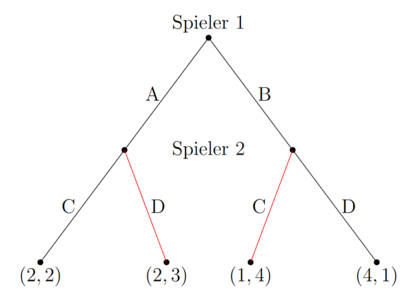
In dem letzten Knotenpunkt, in dem ein Spieler sich entscheiden muss, entscheidet sich Spieler zwei zwiscehn C oder D. Der zweitgenannte Payoff ist der von Spieler 2. Im linken Knoten erhält er bei C 2 und bei D 3. Da 3>2 wählt er im ersten Fall D. Im rechten Knoten erhält er 4 bei C und 1 bei D. Hier wählt er C. Seine Strategie lautet: "Spiele D, wenn der linke (erste) Fall eintritt und wähle C, wenn der zweite (rechte) Fall eintritt".
Spieler 1 weiß, dass das Resultat (A, D) lauten wird, sollte er sich für A entscheiden und (B, C), sollte er sich für B entscheiden. Bei (A, D) erhält er 2 und bei (B, C) erhält er 1. Daher entscheidet sich der rationale Spieler 1 für (A, D).
Das Teilspielperfekte Nash Gleichgewicht lautet:
$TSP\,Nash\,GG=(A,DC)$

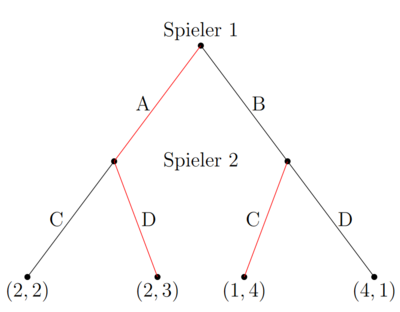
Umwandlung in Normalform

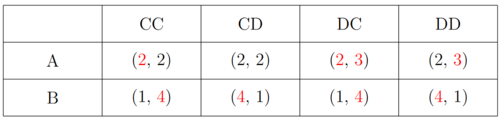
Die Extensivform kann in die Normalform umgewnadelt werden. Hierfür müssen alle reinen Strategien in die bekannte matrix geschrieben werden. Spieler 1 hat lediglich die Strategien $S_{1}=\{A,B\}$. Die Strategien von Spieler 2 sind aufgrund der sequentiellen Form des Spiels anders, als bei statischen Spielen. Die Strategien bestehen aus allen möglichen Antworten auf eine der Strategien von Spieler 1. Spieler 2 hat beispielsweise die Möglichkeit immer C zu spielen. Er hat aber auch die Möglichkeit nur C zu spielen, wenn er A von Spieler 1 beobachtet und sonst D. Alle möglichen Kombinationen von Spieler 2 lauten $S_{2}=\{CC,CD,DC,DD\}$
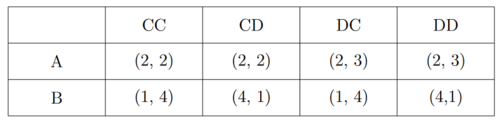
Um die Payoffs zu befüllen müssen die Payoffs der Extensivform herangezogen werden. Für Spieler 2 ist entscheiden, ob der Spieler 1 A oder B spielt. Spielt Spieler 1 A, entscheidet er sich für den erst genannten Buchstaben, spielt Spieler 2 B, entscheidet er sich wiedrum für den zweitgenannten Buchstaben. Muss beispielsweise der Payoff von (A, CD) befüllt werden, kann der Spielbaum von oben entsrechend verfolgt werden. Spieler 1 wählt A, deshalb spielt Spieler 2 C. Der Payoff lautet (2, 2).
Es ergibt sich:

Nash Gleichgewicht

Ein Nash Gleichgewicht liegt für $(s_{1}^{*},s_{2}^{*})$ vor, wenn $U_{1}(s_{1}^{*},s_{2}^{*})\geq U_{1}(s_{i},s_{2}^{*})$ und $U_{2}(s_{1}^{*},s_{2}^{*})\geq U_{2}(s_{1}^{*},s_{i})$ für $s_{i}\in S$ gilt.
In der Normalform lassen sich alle Nash Gleichgewichte eines sequentiellen Spiels mit der bekannten Methode finden (siehe dafür hier). In dem Beispiel von oben ergibt sich als Nash Gleichgewicht (A, DC).


Das teilspielperfekte Nash Gleichgewicht ist in dem vorliegenden Fall auch das einzige Nash Gleichgewicht. Jedes teilspielperfekte Nash Gleichgewicht ist zwar immer auch ein Nash Gleichgewicht, jedoch ist nicht jedes Nashgleichgewicht auch immer teilspielperfekt. Hierfür soll ein zweites sequentielle Spiel dienen, bei dem lediglich ein Payoff geändert wurde (in Extensivform blau markiert).

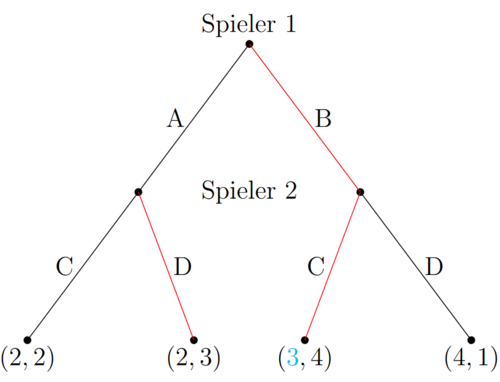
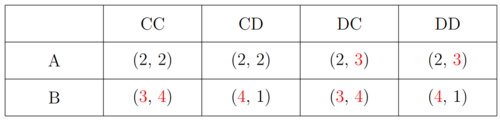
Das Teilspielperfekte Nash Gleichgewicht lautet (B, DC) und die Nash Gleichgewichte sind NG=(B, CC), (B, DC). Dieses Beispiel zeigt, dass auch Nash Gleichgewichte existieren, die nicht teilspielperfekt sind. Dies liegt daran, dass sie unglaubwürdig sind. (B, CC) würde implizieren, dass Spieler 2 C wählt, falls Spieler 1 A wählt. Dies ist aber in dem Sinne unrealistisch, da Spieler 2 für den Fall einen höheren Payoff erhält, wenn er D spielt.

Dominante Strategien

Eine Strategie ist dominant, wenn sie einen höheren oder gleich großen Payoff bietet als alle anderen Strategien, unabhängig davon, welche Strategie der andere Spieler wählt. In sequentiellen Spielen können Strategien ebenfalls dominant sein. Ist eine Strategie dominant, muss die Strategie Teil des Gleichgewichts sein. Das Prinzip der Dominanz wird hier ausführlicher und mit Beispielen erläutert.

MC Fragen

Welche der folgenden Aussagen ist falsch?

	Nicht jedes Gleichgewicht in dominanten Strategien des Spiels in Normalform ist auch ein teilspielperfektes Nash-Gleichgewicht des Spiels in extensiver Form.
	Nicht jedes Nash-Gleichgewicht des Spiels in Normalform ist auch ein teilspielperfektes Nash-Gleichgewicht des Spiels in extensiver Form.
	Nicht jedes teilspielperfekte Nash-Gleichgewicht eines Spiels in extensiver Form ist auch ein Nash-Gleichgewicht des Spiels in Normalform.

Welcher Outcome ist ein teilspielperfektes Nash Gleichgewicht?

	(A, DD)
	(B, DC)
	(A, CD)
	(A, CC)
	(B, DD)
	(B, CC)

Welches Nash Gleichgewichte aus dem sequentiellen Spiel oben ist nicht weilspielpwerfekt??

	(A, DD)
	(B, DC)
	(B, CD)
	(B, DD)
	(A, CD)
	(A, DC)