Spiele
Definition
Ein Spiel ist eine Situation, in der Spieler (Teilnehmer) strategische Entscheidungen treffen, die die Handlungen und Reaktionen der Mitspieler mit einbezieht.
Strategien
Ein Spieler hat mehrere Möglichkeiten, wie er in bestimmten Situationen entscheidet. Diese Möglichkeiten werden Strategien gennant. Ein Spieler entscheidet sich für eine Strategie () aus allen möglichen Strategien (). Die mathematische Schreibweise lautet . Dies bedeutet nichts anderes als dass die gewählte Strategie neben anderen Strategien zur Auswahl stand. Alle möglichen Strategien werden innerhalb einer geschwungenen Klammer dargestellt .
Beispiel: Beim bekannten "Schere Stein Papier" Spiel hat jeder Spieler drei Möglichkeiten, von denen er sich für eine entscheiden muss. Die Spieler wählen beide aus , wobei .
Statische und Sequentielle Spiele
Statische Spiele
Statische Spiele sind Spiele, bei denen die Spieler ihre Strategie gleichzeitig wählen. Ein Beispiel für ein statisches Spiel ist Schere/Stein/Papier. Beide Spieler müssen sich gleichzeitig für eine Strategie entscheiden. Sie können dmentsprechend nicht beobachten, wie der andere Spieler agiert, bzw. für welche Strategie sich der andere Spieler entscheidet. In anderen Fällen treffen die Spieler ihre Entscheidungen nicht gleichzeitig, können aber dennoch nicht beobachten, wie der andere Spieler handelt. Schreibt beispielsweise erst Spieler 1 seine gewählte Strategie auf einen Zettel, lässt diesen zugedeckt und erst dann entscheidet sich Spieler 2, ist dies dennoch ein statisches Spiel.
Sequentielle Spiele
Sequentielle Spiele (auch dynamische Spiele) sind Spiele, bei denen die Spieler aufeinanderfolgend ihre Strategie spielen. Ein Spieler beginnt und und ein zweiter Spieler zieht nach. Der große Unterschied zu den statischen Spielen liegt darin, dass die Spieler die Handlungen der anderen Spieler beoabchten können. Schach ist beispielsweise ein sequentielles Spiel. Der Spieler mit den weißen Figuren (Spieler 1) macht den ersten Zug und der Spieler mit den schwarzen Figuren (Spieler 2) kann den Zug beobachten. Daraufhin zieht er seinen Zug, den wiederum Spieler 1 beobachten kann usw.
Normalform und Extensivform
Spiele sind entweder statisch oder sequentiell. Uanbhängig ob das Spiel sequentiell oder statisch ist, kann es als Normalform oder als Extensivform grafisch dargestellt werden.
Normalform
Bei der Normalform ist Spieler 1 der Zeilenspieler und Spieler 2 der Spaltenspieler. Spieler 1 beeinflusst in welcher Zeile der Ausgang des Spiels ist und Spieler 2 in welcher Spalte. Der erstgenannte Payoff ist der von Spieler 1 und der zweitgenannte von Spieler 2. Häufig werden statische Spiele in der Normalform dargestellt.
Für die Analyse welcher Ausgang von rationalen Spielern erwartet werden kann und wie die Normalform in die extensive Form übersetzt wird, siehe hier.
Extensivform
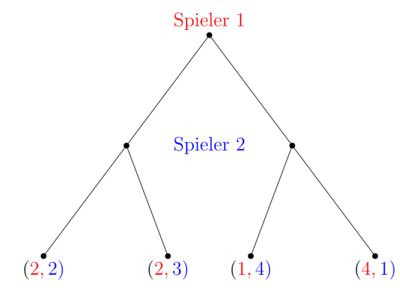
Die Extensivform eines Spiels ist auch als Spielbaum bekannt. In jedem Knotenpunkt trifft ein Spieler eine Entscheidung. Ein Spieler trifft seine Wahl, die in einen der möglichen Punkte eine Etage tiefer endet. In diesem Punkt trifft der zweite Spieler seine Entscheidung, die wiederum erneut in einen Entscheidungsknoten mündet. In dem unten grafisch dargestellten Beispiel hat jeder Spieler nur eine Entscheidung zu treffen, weshalb nach der Entscheidung von Spieler 2 die Payoffs feststehen. Der erstgenannte Payoff ist der des Spielers, der angefangen hat und der zweitgenannte der des Nachzüglers.
Für die Analyse welcher Ausgang von rationalen Spielern erwartet werden kann und wie die Extensivform in die Normalform übersetzt wird, siehe hier.
Beste Antwort
Die Beste Antwort ist ein Konzept, bei dem untersucht wird welche Strategie eines Spielers die Beste Antwort auf die Strategie eines anderen Spielers ist. In dem Beispiel der Normalfomr oben ist ist die Frage: Was ist die beste Antwort von Spieler 1 auf die Verrat-Strategie und die Schweigen Strategie von Spieler 2. Für die Beantwortung wird betrachtet, welcher Payoff von Spieler 1 am größten ist, wenn Spieler 2 Verrat spielt. Spielt Spieler 2 verrat, erhält Spieler 1 einen Payoff von -5, wenn er auch Verrat spielt und einen Payoff von -10, wenn er Schweigen spielt. Da -5 größer ist als -10, ist die Beste Antwort von Spieler 1 auf Verrat ebenfalls der Verrat. Mit der selben Vorgehensweise lässt sich herausfinden, dass die Beste Antwort von Spieler 1 auf Schweigen des Spielers 2 Verrat lautet.
Dominanz der Strategien
Eine Strategie ist dominant, wenn diese Strategie ungeachtet der Reaktion der anderen Spieler immer zu einem größeren Payoff (das kann ein Nutzenniveau, Geld oder etwas anderes sein) als alle anderen Strategien führt. Als Beispiel soll die oben dargestellte Normalform dienen. Zur Vereinfachung soll nur untersucht werden, ob Spieler 1 (der Zeilenspieler) eine dominante Strategie hat. Daher wird nur der Payoff von Spieler 1 angegeben. Außerdem ist es irrelevant wie die Strategien des Spieler 2 lauten, deshalb lautet die erste Spalte einfach nur noch A und die zweite Spalte nur noch B.
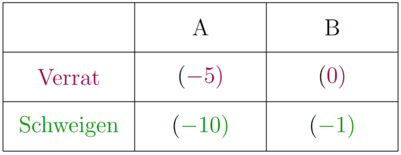
Ist eine der beiden Strategien für Spieler 1 dominant, so ist diese Strategie immer besser. Sollte sich der SPieler 2 für die erste zweite Spalte entscheiden, bringt eine dominante Strategie genauso den größten Payoff der Spalte, wie wenn sich der Spieler zwei für die zweite Spalte entscheidet. In dem oben dargestellten Beispiel ist der Payoff in Spalte A größer, wenn sich Spieler 1 für Verrat entscheidet (-5>-10). Auch in Spalte B ist der Payoff von Verrat größer als der von Schweigen (0>-5). Egal wie sich der Spieler 2 entscheidet, Spieler 1 sollte immer Verrat spielen. Verrat ist eine dominante Strategie und Schweigen eine dominierte Strategie. Damit knüpft der Dominanzbegriff sehr sark an des Konzept der Besten Anwtort an.
Es wird zwischen strikter dominanz und schwacher Dominanz unterschieden. Das oben dargestellte Beispiel stellt strikte Dominanz dar, denn jeder Payoff des Verrats ist strikt größer als der des Schweigens. Schwache Dominanz würde vorliegen, wenn die Payoffs größer oder gleich groß sind, solange mindestens ein Payoff strikt größer ist.
