Gradientenmethode

Die Gradientenmethode ist eine Methode zur Bestimmung eines Maximums/Minimus mit einer Nebenbedingung. Hierfür wird das Skalarprodukt zweier Vektoren gebildet. Der erste Vektor ist die Richtung der Budgetgeraden und der andere Vektor ist der Gradient des Nutzenfunktion, welcher in Richtung des steilsten Anstiegs zeigt. Die Gradientenmethode ist neben dem Lagrangeverfahren eine weitere Möglichkeit zur Bestimmung eines Tangentialpunktes.

Gradient

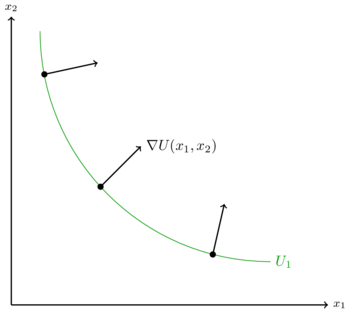
Der Gradient ist ein Vektor, welcher in Richtung des steilsten Anstiegs zeigt. Er lässt sich bilden, indem eine multivariate Funktion partiell abgeleitet wird. Im Falle einer Nutzenfunktion mit zwei Konsumgütern $x_{1}$ und $x_{2}$ lässt sich der Gradient wie folgt bestimmen:

$\nabla =(\partial U(x_{1},x_{2})/\partial x_{1},\quad \partial U(x_{1},x_{2})/\partial x_{2})^{T}$ 

Je nach Konsumpunkt $(x_{1},x_{2})$ zeigt der Gradient in eine andere Richtung. Die partielle Ableitung nach $x_{1}$ eingesetzt an dem jeweiligen Punkt bestimmt, wie weit der Vektor in die $x_{1}$-Richtung geht. Die partielle Ableitung nach $x_{2}$ bestimmt für den jeweiligen Punkt, wie weit der Vektor in die $x_{2}$-Richtung verläuft.

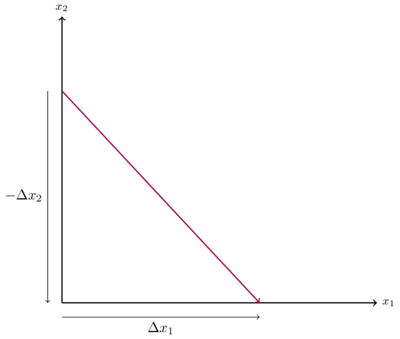
Vektor der Budgetgeraden

Die Budgetgerade lässt sich in einen Vektor umschreiben. Für die $x_{1}$-Richtung lässt sich beispielsweise die Differenz von $x_{1}=0$ und $x^{max}$ nehmen. Für die $x_{2}$-Richtung kann wiederum die Differenz zwischen $x_{2}^{max}$ und $x_{2}=0$ herangezogen werden.
Es ergibt sich:

${\vec {v}}=(x_{1}^{max}-0,\quad 0-x_{2}^{max})^{T}=(x_{1}^{max},\quad -x_{2}^{max})^{T}$ 

Der Vektor ${\vec {v}}$ lässt sich in der Grafik unten erkennen. Es gilt zu beachten, dass der Vektor, anders als der Gradient, nicht variabel in $x_{1}$ und $x_{2}$ ist.

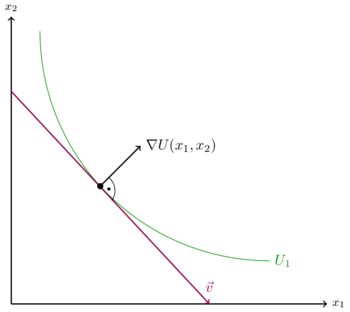
Tangentialpunkt

Das Skalarprodukt zweier Vektoren ist gleich null, wenn die zwei Vektoren orthogonal zueinander verlaufen. Exakt diese Eigenschaft liegt im Tangentianlpunkt vor. Der Gradient verläuft im Tangentialpunkt der Indifferenzkurve und der Budgetgeraden orthogonal zu dem berechneten Vektor ${\vec {v}}$ Die Tangentialbedingung lässt sich somit auch durch das Skalarprodukt herleiten:

$\nabla U(x_{1},x_{2})^{T}\cdot {\vec {v}}{\stackrel {!}{=}}0$ 

Die daraus resultierende Relation zwischen $x_{1}$ und $x_{2}$ ist dieselbe, wie bei dem Lagrangeverfahren und kann in die Budgetrestriktion eingesetzt werden, um die optimale Nachfrage zu erhalten.

Beispiel

Die Nutzenfunktion lautet $U(x_{1},x_{2})=x_{1}\cdot x_{2}$. Die Preise lauten $p_{1}=2$ und $p_{2}=4$. Insgesamt steht ein Budget von 20 Euro zur Verfügung

Gradient

Der Gradient lautet $\nabla =(x_{2},\quad x_{1})^{T}$

Budgetvektor

Der Budgetvektor lautet ${\vec {v}}=({\frac {20}{2}},\quad -{\frac {20}{4}})^{T}=(10,\quad -5)^{T}$

Tangentialpunkt

Für den Tangentialpunkt muss das Skalarprodukt null sein: $(x_{2},\quad x_{1})\cdot (10,\quad -5)^{T}{\stackrel {!}{=}}0$
$10x_{2}-5x_{1}=0$
Die Tangentialbedingung lautet demenstprechend $x_{1}=2x_{2}$

Optimale Nachfrage

Die Tangentialbedingung kann in die Budgetrestriktion eingesetzt werden $2x_{1}+4x_{2}=20\quad \Leftrightarrow \quad 8x_{2}=20$
Die optimale Nachfrage lautet $(x_{1}^{*},x_{2}^{*})=(5,\quad 2.5)$